经典题：最大子序列和

诶咦

已于 2023-07-06 11:57:07 修改

阅读量73

点赞数

分类专栏：数据结构与算法文章标签： c++ 数据结构算法

于 2023-07-06 02:15:41 首次发布

本文链接：https://blog.csdn.net/qq_73643549/article/details/131565980

版权

数据结构与算法专栏收录该内容

4 篇文章 0 订阅

订阅专栏

题目描述：

取自leetcode--53.

2. 抛开效率，直观地想

从直观的角度，或者说一般的想法。我们只需要枚举所有的区间，并进行求和，再求取最大值即可。

稍微加一点数学的佐料，我们定义一个区间往往需要两个维度[点，长度]/[起点，终点]

从第一个定义方案来设计，我们就有以下代码：

//INF表示无穷大
int MaxSum1(const vector<int>& arr) {
	int max = -INF;
	int n = arr.size();
	
	for (int len = 1; len <= n; ++len)//枚举长度
	{
		for (int i = 0; i < n; ++i)//枚举起点
		{
			int sum = 0;
			int end = i + len;//计算终止坐标
			for (int j = i; j < end && j < i + n; ++j)//求和循环
			{
				sum += arr[j];
			}

			if (max < sum) max = sum;//求取最大值
		}
	}

	return max;//返回答案
}

这里我们也很容易知道时间复杂度为O(N(N + 1)(N + 2)/2) -- O(N^3);

第一种表示，因为确定区间靠长度和点，而至于先确定那个无所谓！也就是说其实可以这样子写。

int MaxSum1(const vector<int>& arr) {
	int max = -INF;
	int n = arr.size();
	

	for (int i = 0; i < n; ++i)//枚举起点
	{
	    for (int len = 1; len <= n; ++len)//枚举长度
	    {
			int sum = 0;
			int end = i + len;//计算终止坐标
			for (int j = i; j < end && j < i + n; ++j)//求和循环
			{
				sum += arr[j];
			}

			if (max < sum) max = sum;//求取最大值
		}
	}

	return max;
}

这里我们也可以感觉到这里存在冗余！也就是在第二种写法中，枚举长度是多余的。因为我们就是靠[点，点]固定区间，只不过这个点中有一个需要我们计算。

接下来我们换一种表示方案[点，点]：

int MaxSum1(const vector<int>& arr) {
	int max = -INF;
	int n = arr.size();
	
	for (int i = 0; i < n; ++i)//枚举起点
	{
		int sum = 0;
		for (int j = i; j < n; ++j)//确定尾巴，求和取大
		{
			sum += arr[j];
            if (max < sum) max = sum;//求取最大值
		}
	}

	return max;
}

至此我们就优化出了O(N^2);

我们可以认为这是另外一种表示形式，也可以认为这是第一种表示形式取消冗余的结果，读者可以根据自己的理解选取；

再思考，拆解问题

状态相依，压缩成“簇”

以上是我们直接的求取方法，但是这一定就好吗？能不能再优化？

优化的前提有：压缩可状态，状态转移可表达。

状态能压缩吗？

我们先来打个表：

j\i	1	2	...	n
1	sum[1,1]	sum[1,2]		sum[1,n]
2	/	sum[2,2]		sum[2,n]
...	/
n	/	/	/	sum[n,n]

我们现在有两个压缩方向行和列。以列压缩为例子(行压缩也是可行的)。

假设我们可以压缩原来所有的状态为 sum[j] 存放以j为终端的区间最大和

那么我们的答案诞生在ans = max{sum[j]}；

目前来看，一切完美就差一点，如何保证sum[j]存放的就是以j为终端的最大区间和。

从[点，点]表述的直观方法我们可以知道，或者说从上表行的方向可以想到状态转移。换种角度，我们压缩了列信息，而状态转移方程表示中必定是当前状态与其他状态的关系！列动成行，这也表明转移方向的思考维度是行；

sum[j] = max{sum[j-1] + a[j], a[j]} = max{sum[j-1] , 0} + a[j];

对于sum[j-1] + a[j]来说他是将s[i,j-1]的一组区间和扩展到sum[i,j],其中i<j;

对于a[j]来说，它补全了上式缺失的sum[j,j]；

int MaxSum3(const vector<int>& arr) {
	int max;
	int n = arr.size();
	vector<int> sum(n);
    max = sum[0] = arr[0];//初始化
	
    //动态规划，因为压缩的是列信息所以从前往后
    for(int i = 1; i < n; ++i)
    {
        sum[i] = max(sum[i-1] + arr[i], arr[i]);
        max = max(max, sum[i]);
    }

	return max;
}

我们也给出压缩行信息的编码：

int MaxSum3(const vector<int>& arr) {
	int max;
	int n = arr.size();
	vector<int> sum(n);
    max = sum[n-1] = arr[n-1];//初始化
	
    //动态规划，因为压缩的是行信息所以从后往前
    for(int i = n - 2; i >= 0; --i)
    {
        sum[i] = max(sum[i+1] + arr[i], arr[i]);
        max = max(max, sum[i]);
    }

	return max;
}

至此我们完成了O(n)的时间复杂度程序。

这里体现的重要思考维度就是"压缩"，如何将数据合理压制成“簇”(集合)来管理是很重要的学问。

压缩的方式还有很多，如二进制压缩，Huffman树也是一种压缩，并查集提供的压缩思路。

分而治之

分而治之的拆解思路较为简单。如果是动态规划(递推)是扩展已知状态，直至包含目标状态为止；

那么分而治之的递归，则是拆解问题，直至转移到已知可解集；

分治的方案有很多，就像二分的方式有很多。或者说，它们是同源的。

但很显然，这里我们只能二分区间。

思路如下，采取典型的分、合步骤走：

分：求解出左部分区间和，右部分区间和；

合：跨区域最大区间和

最终三者求大即为答案；

故此可以编写代码：

ll MaxSum(vector<ll>& arr, int left, int right) {
	if (left == right)//基准情形,一个元素
	{
		return arr[left];//一个元素，返回自身
	}

	int center = (left + right) / 2;
	int leftMaxSum = MaxSum(arr, left, center);
	int rightMaxSum = MaxSum(arr, center + 1, right);

    //跨区求和
    //以center为终点向左扩展取得最大值
	int leftBoundMaxSum = -INF, leftBoundSum = 0;
	for (int i = center; i >= 0; --i)
	{
		leftBoundSum += arr[i];
		if (leftBoundMaxSum < leftBoundSum) leftBoundMaxSum = leftBoundSum;
	}

    //以center+1为起点，向右扩展取得最大值
	int rightBoundMaxSum = -INF, rightBoundSum = 0;
	for (int i = center + 1; i <= right; ++i)
	{
		rightBoundSum += arr[i];
		if (rightBoundMaxSum < rightBoundSum) rightBoundMaxSum = rightBoundSum;
	}

	return max(max(leftMaxSum, rightMaxSum), leftBoundMaxSum + rightBoundMaxSum);
}

接下来我们分析一下复杂度：

假设函数的时间复杂为T(n);

那么有方程 T(n) = 2T(n/2) + n;，其中T(1) = 1

递推得到T(n) = 2^k * 1 + kn; 其中n/2^k = 1;所以k = logn

T(n) = O(nlogn + n);

那么对于这道题这个复杂对是不能够过关的。因为nlogn的解决范围是10^5.

那能否优化呢？我们注意到如果再求取跨区间最大和的时候能降低复杂度，那么分而治之将得到很大的提升。

如果我们早就记录下，我们的需要的数值，那么我们就可以把这部分复杂度将为O(1);

于是设计struct struts{}；

//记录区间[l,r]需要记录的数据，标注如下

struct Status {

int lSum；//记录以左端l为起点的最大区间和

int rSum;//记录以右端点r为终点的最大区间和

int mSum;//记录最大区间和

int iSum;//记录区间合

};

接下来讲解状态的转移：

对与mSum的维护是一样的；对于iSum的维护也比较简单就是iSum = l.iSum + r.iSum;

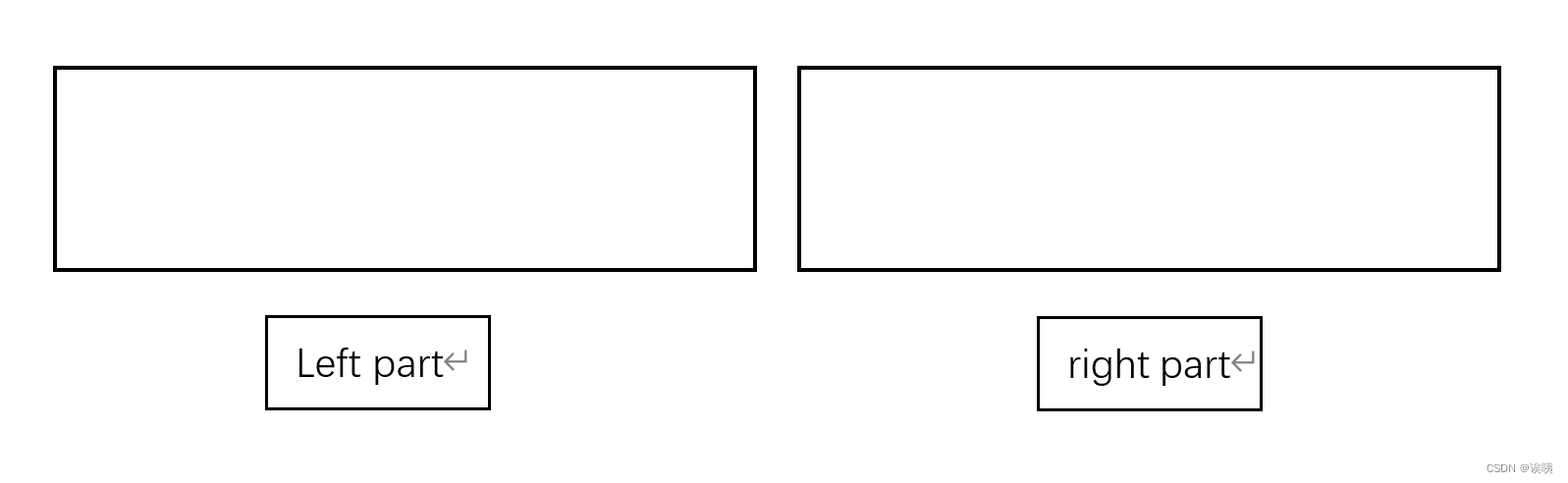
对于lSum的维护，见图：

新的lSum再上述两图两种状态中，也就是跨区域和旧值

lSum = max(l.lSum, l.iSum + r.lSum);

同理，rSum = max(r.rSum, r.iSum + l.rSum);

//记录区间[l,r]需要记录的数据，标注如下

struct Status {

        int lSum；//记录以左端l为起点的最大区间和

        int rSum;//记录以右端点r为终点的最大区间和

        int mSum;//记录最大区间和

        int iSum;//记录区间合

};

Status get(vector<int> &a, int l, int r) {
    if (l == r) {
        return (Status) {a[l], a[l], a[l], a[l]};//一个元素时的状态
    }

    int m = (l + r) >> 1;
    Status lSub = get(a, l, m);//获得左区间数据
    Status rSub = get(a, m + 1, r);//获得右区间数据

    //合并成新区间，也可以封装函数
    int iSum = lSub.iSum + rSub.iSum;
    int lSum = max(lSub.lSum, lSub.iSum + rSub.lSum);
    int rSum = max(rSub.rSum, rSub.iSum + lSub.rSum);
    int mSum = max(max(lSub.mSum, rSub.mSum), lSub.rSum + rSub.lSum);
    return (Status) {lSum, rSum, mSum, iSum};
}

Status MaxSum(vector<ll>& arr, int left, int right){
    return get(arr, left, right);
}

此时我们的时间复杂度就为O(n + logn);

题外话：

虽然分治法也可以优化到O(n)的层级，但对于这道题，它不是最优解。

如果仔细观察，分治法的最优解其实是在O(N)层级内计算了任意一个子区间的最大区间和。

如过我们将这些值记录下来，存入堆中，那么我们再查看后续任意一个区间的值，将可以降低到O(logn);