目录
在数据科学和机器学习的世界里,我们经常需要处理大量的高维数据。然而,高维数据不仅会增加计算成本,还可能因为维度灾难(Curse of Dimensionality)而导致模型性能下降。为了解决这个问题,主成分分析(PCA)成为了一个强大的工具,它可以帮助我们降低数据的维度,同时保留数据中的大部分信息。
一、什么是PCA?
PCA是一种无监督的线性变换方法,它通过正交变换将原始数据转换为一组线性不相关的变量,即主成分。这些主成分按照方差从大到小排序,第一个主成分具有最大的方差,后面的主成分方差依次减小。通过选择前几个方差较大的主成分,我们可以在保持数据主要特性的同时,大大减少数据的维度。
二、PCA相关概念
2.1 向量内积
- 定义:两个向量之间的点积或数量积,表示一个向量在另一个向量方向上的投影长度与另一个向量模长的乘积。
- 物理含义:设向量A和向量B,A在B向量上的投影乘以B向量的模(长度)即为A与B的内积值。当向量B的模为1时,内积值等于A向B所在直线投影的矢量长度。
2.2 基变换
- 基:在二维空间中,(1,0)和(0,1)构成一组基,基是正交的(即内积为0,或相互垂直),且线性无关。
- 基变换定义:数据与一个基做内积运算,结果作为第一个新的坐标分量;然后与第二个基做内积运算,结果作为第二个新坐标的分量。
- 矩阵相乘的意义:将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去。
2.3 方差
- 定义:衡量随机变量或一组数据与其平均值偏离程度的度量。
- 计算公式:对于样本的特征a,方差D(a)是各数值与其平均数之差的平方和的平均数。
- 意义:方差越小,数据的取值越集中;方差越大,数据的取值越分散。
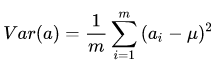
为了方便处理,我们将每个变量的均值都化为 0 ,因此方差可以直接用每个元素的平方和除以元素个数表示:
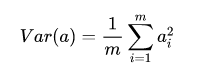
于是上面的问题被形式化表述为:寻找一个一维基,使得所有数据变换为这个基上的坐标表示后,方差值最大。
2.4 协方差
- 定义:衡量两个随机变量之间线性关系的强度和方向。
- 计算公式:两个变量的协方差等于它们与其各自平均值之差的乘积的平均值。
- 作用:协方差为正值时,表示两者正相关;为负值时,表示两者负相关;为0时,表示两者没有线性关系。
协方差公式为:
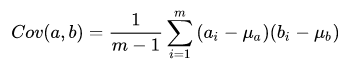
当样本数较大时,不必在意其是 m 还是 m-1,为了方便计算,我们分母取 m。
当协方差为 0 时,表示两个变量完全独立。为了让协方差为 0,我们选择第二个基时只能在与第一个基正交的方向上进行选择,因此最终选择的两个方向一定是正交的。
至此,我们得到了降维问题的优化目标:将一组 N 维向量降为 K 维,其目标是选择 K 个单位正交基,使得原始数据变换到这组基上后,各变量两两间协方差为 0,而变量方差则尽可能大(在正交的约束下,取最大的 K 个方差)。
2.5 协方差矩阵
- 定义:对于n维随机变量(X1, X2,..., Xn),其协方差矩阵是一个n×n的矩阵,其中元素cij是第i个和第j个特征的协方差。
- 在PCA中的作用:协方差矩阵的特征向量和特征值对于选择主成分至关重要。特征值的大小反映了对应特征向量上数据变化的程度,特征值越大,该方向上的变化越大,越能体现数据的特征。
假设我们只有 a 和 b 两个变量,那么我们将它们按行组成矩阵 X:
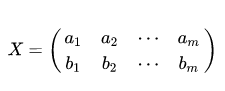
然后:
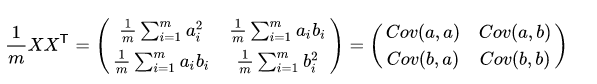
我们可以看到这个矩阵对角线上的分别是两个变量的方差,而其它元素是 a 和 b 的协方差。两者被统一到了一个矩阵里。
三、PCA在机器学习中的应用
PCA在机器学习中有着广泛的应用,以下是一些常见的场景:
-
数据降维:通过PCA降维,我们可以减少数据的维度,降低计算成本,同时保留数据中的主要信息。这对于高维数据的可视化、聚类、分类等任务非常有用。
-
特征提取:PCA可以作为一种特征提取方法,从原始数据中提取出最具代表性的特征。这些特征通常具有较低的维度,但能够很好地描述数据的本质特性。
-
去噪和压缩:PCA可以通过去除噪声和冗余信息来压缩数据。在图像处理中,PCA可以用于图像压缩和去噪,减少图像数据的大小并提高图像质量。
-
异常检测:由于PCA能够捕捉数据中的主要变化模式,因此它可以用于异常检测。通过比较新数据与PCA模型预测的数据之间的差异,我们可以识别出异常值或异常模式。
四、代码实例:
手动实现PCA
计算协方差矩阵:
cov_matrix = np.cov(standardized_X, rowvar=False)计算特征值和特征向量:
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)选择主成分:
sorted_indices = np.argsort(eigenvalues)[::-1]
selected_indices = sorted_indices[:num_components]
principal_components = eigenvectors[:, selected_indices]投影:
reduced_X = np.dot(standardized_X, principal_components)降维结果:
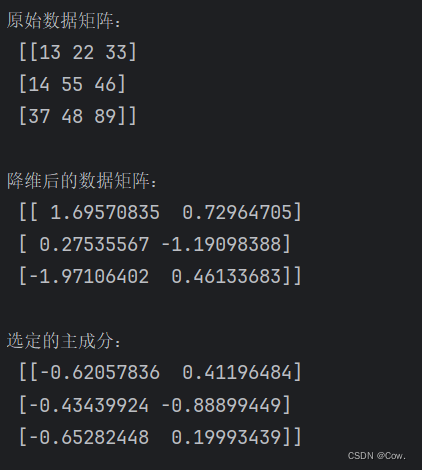
人脸降维实例:
from PIL import Image
import os
import numpy as np
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
# 指定图像文件夹路径
image_folder_path = "D:/pcaphoto"
# 获取文件夹中所有图像文件名
image_files = [f for f in os.listdir(image_folder_path) if f.endswith(".jpg")]
image_data = []
for image_file in image_files:
# 读取图像并转换为灰度图像
image_path = os.path.join(image_folder_path, image_file)
image = Image.open(image_path).convert("L")
gray_image = np.array(image)
# 将灰度图像展平
image_flattened = gray_image.flatten().astype(float)
# 标准化数据
scaler = StandardScaler()
image_scaled = scaler.fit_transform(image_flattened.reshape(-1, 1))
# 使用PCA进行降维
pca = PCA(n_components=1) # 将维度设置为1
image_pca = pca.fit_transform(image_scaled)
# 将降维后的数据保存在列表中
image_data.append(image_pca)
# 汇总所有降维后的数据
all_images_pca = np.concatenate(image_data)
# 反向转换并重建图像
all_images_reconstructed = pca.inverse_transform(all_images_pca)
all_images_reconstructed = scaler.inverse_transform(all_images_reconstructed)
all_images_reconstructed = all_images_reconstructed.reshape(-1, gray_image.shape[1])
# 显示合并的重建图像
reconstructed_image = Image.fromarray(np.uint8(all_images_reconstructed))
reconstructed_image.show()降维前后图片对比:

结果分析:
先将原图像转为灰度图像
经过降维,部分特征值已经被舍弃了,所以原数据图像更清晰。
五、PCA的优缺点
优点:
- 简单易实现:PCA是一种简单且易于实现的算法,它不需要任何参数调整或模型训练。
- 可解释性强:PCA降维后的主成分具有明确的数学意义,可以解释数据中的主要变化模式。
- 稳定性好:PCA对数据中的噪声和异常值具有较好的鲁棒性,因此在实际应用中表现出较好的稳定性。
缺点:
- 对非线性数据效果不佳:PCA是一种线性变换方法,对于非线性数据可能无法有效地捕捉数据中的复杂结构。
- 对数据分布敏感:PCA的性能受到数据分布的影响,如果数据分布不均匀或存在异常值,可能会导致PCA的效果不佳。
- 丢失部分信息:PCA在降维过程中会丢失部分信息,这可能导致一些细节或微小差异被忽略。
六、总结
PCA作为一种简单而有效的数据降维方法,在数据分析、机器学习等领域得到了广泛的应用。通过本文的介绍,相信大家对PCA的原理、步骤和应用场景有了更深入的了解。在实际应用中,我们可以根据具体需求选择合适的降维方法,以提高数据分析的效率和准确性。






















 3万+
3万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








