数学建模之图论建模

目录

一、最小生成树问题

二、最短路径问题

三、匹配问题：

四、最大流问题

五、最小费用问题：即在最大流问题上，增加“费用”条件

---

仅做学习使用 

一、最小生成树问题

对应问题：管道铺设，通信网络铺设

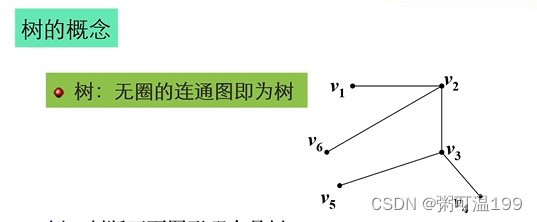
求网络D的生成树，使其权和最小

方法（避圈法（Kruskal，1956），破圈法（管梅谷，1975））

一、避圈法：一种选点和选边的过程

法一，

 法二，

 

 二、破圈法：见圈就破，去掉其中权最大的

 python对问题求解

networkx求最小生成树函数为minimum_spanning_tree,其调用格式为：

T=minimum_spanning_tree(G,weight='weight',algorithm='kruskal')
#其中G为输入图，algorithm的取值有三种字符串：'kruskal'（默认值）,'prim',或'boruvka'
#即对应三总算法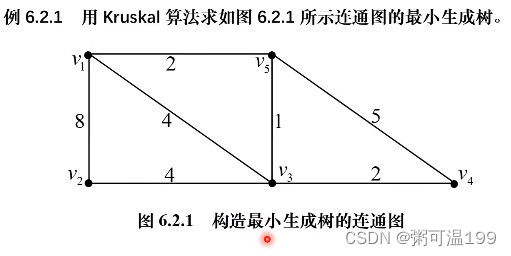

import numpy as np
import networkx as nx
import pylab as plt
L = [(1,2,8), (1,3,4), (1,5,2), (2,3,4), (3,4,2), (3,5,1), (4,5,5)]
b = nx.Graph()
b.add_nodes_from(range(1,6))
b.add_weighted_edges_from(L)
T = nx.minimum_spanning_tree(b) #返回可迭代对象
w = nx.get_edge_attributes(T, 'weight') #提取字典数据
TL = sum(w.values()) #计算最小生成树的长度
print("最小生成树为：", w)
print("最小生成树的长度为：", TL)
pos = nx.shell_layout(b)
nx.draw(T, pos, node_size=280, with_labels=True, node_color='r')
nx.draw_networkx_edge_labels(T, pos, edge_labels=w)
plt.savefig('6.2.1 The minimum spanning tree.png', dpi=500)
plt.show()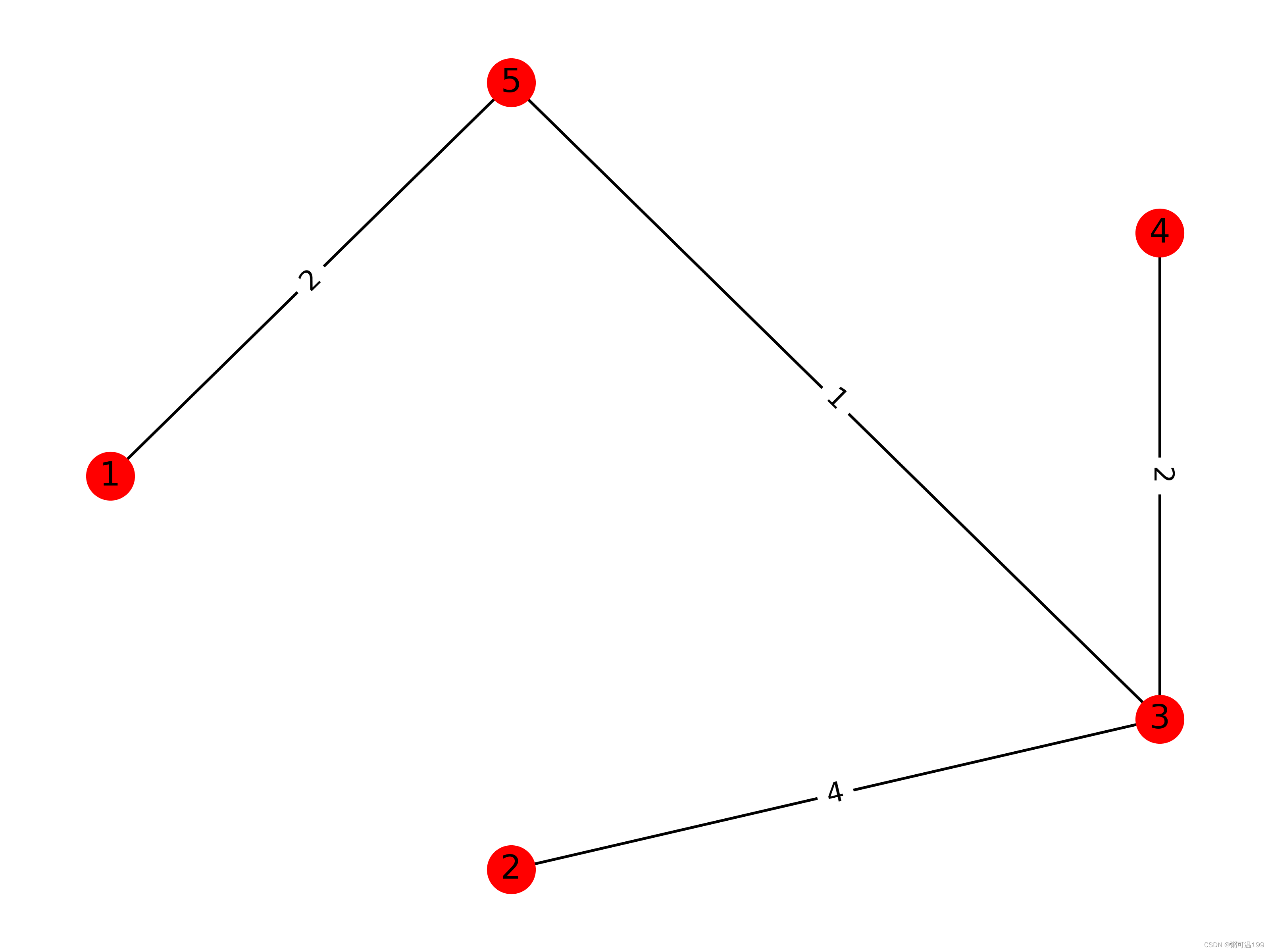

 

 

二、最短路径问题

具体应用：选址，管道铺设线路，设备更新,投资，某些整数规划和动态规划问题，生产生活中运用广泛。

法一：Dijikstra标号法：求两个点的最短距离

 

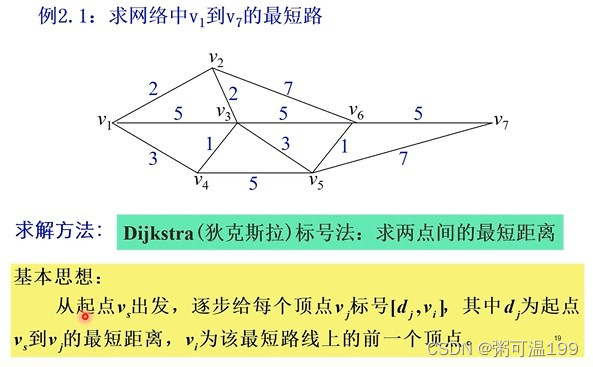
                   3.当网络中存在负的权数时，算法失效。

                   4.有向网络图与无向网络图做法基本一致，仅需注意网络弧的方向

法二：Floyd算法：求所有顶点对间的最短距离

 注：选址问题，选择中心位置

python对问题求解：

network调用函数dijkstra_path（求最短路径），dijkstra_path_length（求最短距离）

 

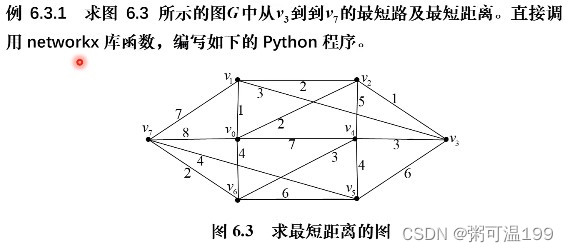
import numpy as np
import networkx as nx

List = [(0,1,1), (0,2,2), (0,4,7), (0,6,4), (0,7,8), (1,2,2), (1,3,3), 
        (1,7,7), (2,3,1), (2,4,5), (3,4,3), (3,5,6), (4,5,4), (4,6,3), 
        (5,6,6), (5,7,4), (6,7,2)]
G = nx.Graph()
G.add_weighted_edges_from(List)
A = nx.to_numpy_matrix(G, nodelist=range(8)) #导出邻接矩阵
np.savetxt('6.3.1 Adjacent matrix.txt', A)
p = nx.dijkstra_path(G, source=3, target=7, weight='weight') #求最短路径
d = nx.dijkstra_path_length(G, 3, 7, weight='weight') #求最短距离
print("最短路径为：", p, "；最短距离为：", d)

若求所有顶点的最短距离

import numpy as np
import networkx as nx
a = np.loadtxt("6.3.1 Adjacent matrix.txt")
G = nx.Graph(a) #利用邻接矩阵构造赋权无向图
d = nx.shortest_path_length(G, weight='weight') #返回值是可迭代类型
Ld = dict(d)  #转换为字典类型
print("顶点对之间的距离为：", Ld)  #显示所有顶点对之间的最短距离
print("顶点0到顶点4的最短距离为：", Ld[0][4]) #显示一对顶点之间的最短距离
m,n = a.shape
dd = np.zeros((m,n))
for i in range(m):
    for j in range(n):
        dd[i,j] = Ld[i][j]
print("顶点对之间最短距离的数组表示为：\n", dd)  #显示所有顶点对之间最短距离
np.savetxt('6.3.2 The shortest path', dd) #把最短距离数组保存到文本文件中
p = nx.shortest_path(G, weight='weight') #返回值是可迭代类型
dp = dict(p)  #转换为字典类型
print("\n顶点对之间的最短路径为：", dp)
print("顶点0到顶点4的最短路径为：", dp[0][4])

 

三、匹配问题：

具体应用：分配任务等等

python对问题求解

最大匹配函数max_weight_matching

 

 

import numpy as np
import networkx as nx
from networkx.algorithms.matching import max_weight_matching
a = np.array([[3,5,5,4,1], [2,2,0,2,2], [2,4,4,1,0], 
              [0,2,2,1,0], [1,2,1,3,3]])
b = np.zeros((10,10))
b[0:5,5:] = a
G = nx.Graph(b)
s0 = max_weight_matching(G) #返回值为（人员，工作）的集合
s = [sorted(w) for w in s0]
L1 = [x[0] for x in s]
L1 = np.array(L1)+1 #人员编号
L2 = [x[1] for x in s] 
L2 = np.array(L2)-4  #工作编号
c = a[L1-1, L2-1] #提取对应的效益
d = c.sum()  #计算总的效益
print("工作分配对应关系为：\n人员编号：", L1)
print("工作编号：", L2)
print("总的效益为：", d)

四、最大流问题

系统中包含的流量问题，如：公路系统有车辆流，控制系统有信息流等等。

 

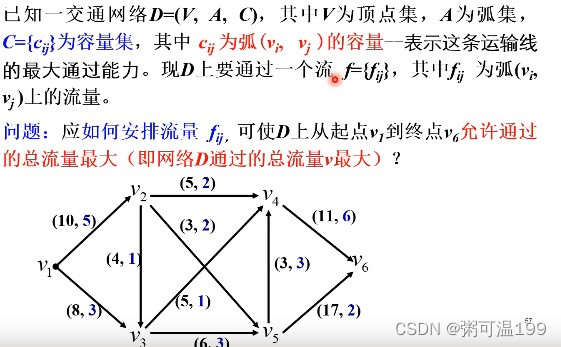
 可行流：满足容量限制约束和平恒条件的流

 基本概念

 

 最大流最小截定理：

                网络的最大流量等于最小截量

 求最大流的方法：

 

 

 python对问题求解： 

运用函数：nx.maximum_flow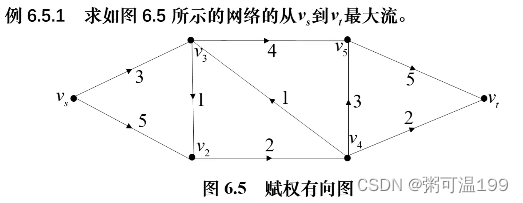 

import numpy as np
import networkx as nx
import pylab as plt
L = [(1,2,5), (1,3,3), (2,4,2), (3,2,1), (3,5,4), 
     (4,3,1), (4,5,3), (4,6,2), (5,6,5)]
G = nx.DiGraph()
for k in range(len(L)):
    G.add_edge(L[k][0]-1, L[k][1]-1, capacity=L[k][2])
value, flow_dict = nx.maximum_flow(G, 0, 5)
print("最大流的流量为：", value)
print("最大流为：", flow_dict)
n = len(flow_dict)
adj_mat = np.zeros((n,n), dtype=int)
for i, adj in flow_dict.items():
    for j, weight in adj.items():
        adj_mat[i,j] = weight
print("最大流的邻接矩阵为：\n", adj_mat)
ni,nj = np.nonzero(adj_mat) #非零弧的两端点编号
key = range(n)
s = ['v'+str(i+1) for i in range(n)]
s = dict(zip(key, s)) #构造用于顶点标注的字符字典
plt.rc('font', size=16)
pos = nx.shell_layout(G) #设置布局
w = nx.get_edge_attributes(G, 'capacity')
nx.draw(G, pos, font_weight = 'bold', labels = s, node_color='r')
nx.draw_networkx_edge_labels(G, pos, edge_labels=w)
path_edges = list(zip(ni, nj))
nx.draw_networkx_edges(G, pos, edgelist=path_edges, edge_color='r', width=3)
plt.show()

五、最小费用问题：即在最大流问题上，增加“费用”条件

具体应用：花“小钱”办“大事” 

寻找费用增加最小的增广链就相当于：在由费用为弧权的有向图中寻找从发点到收点的最短路。

 python对问题求解

运用函数max_flow_min_cost

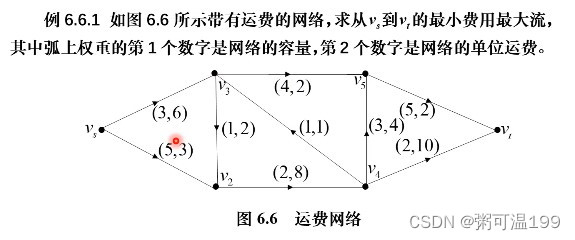
import numpy as np
import networkx as nx
L = [(1,2,5,3), (1,3,3,6), (2,4,2,8), (3,2,1,2), (3,5,4,2), 
     (4,3,1,1), (4,5,3,4), (4,6,2,10), (5,6,5,2)]
G = nx.DiGraph()
for k in range(len(L)):
    G.add_edge(L[k][0]-1,L[k][1]-1,capacity=L[k][2],weight=L[k][3])
mincostFlow=nx.max_flow_min_cost(G,0,5)
print("所求流为：", mincostFlow)
mincost = nx.cost_of_flow(G, mincostFlow)
print("最小费用为：", mincost)
flow_mat = np.zeros((6,6), dtype=int)
for i, adj in mincostFlow.items():
    for j, f in adj.items():
        flow_mat[i,j] = f
print("最小费用最大流的邻接矩阵为：\n", flow_mat)