算法（六）最短路径之Dijkstra算法

前言

在上一篇博客中，我们学习了最短路径系列的第一种算法Floyd-Warshall算法来求解图中点与点之间的最短路径的问题。这篇博客我们就要来学习一下，求解单源最短路径的一种算法：Dijkstra算法。

具体问题

还是几个城市间的最短路径问题，这次我们需要求的是1号顶点到其余个点的最短路径。路径图如下

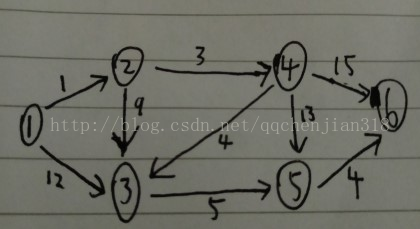
现在我们需要求解1号点到2、3、4、5、6号点的最短路径。

Dijkstra算法

          图的数据化

       同样通过一个二维数组来保存图的数据

       

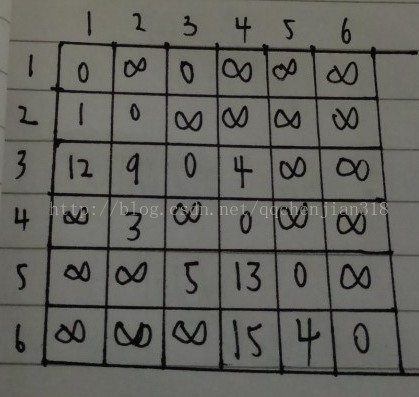
      (和上篇博文相同，1到1为0表示是同一个点，2到1是无穷符号，表示两个点暂时没有路径联通，1到2是1，表示1到2的距离是1)

        算法分析过程

      首先，我们求解的是1号点到其余个点的距离，所以我们可以用一个一维数组来保存这些数据

    int[] dis = {0,0,1,12,999999,999999,999999};

       明明是一共6个点，我们这里为什么是七个数据呢？那是为了便于编码，我们默认dis[0]是没有意义的，所以编码时，从dis[1]开始，dis[1] = 0，表示1到它自己是0，dis[2] = 1,表示1到2的距离是1。

        所以以后我们就把第一个0默认省掉，直接表示为

   int[] dis = {0,1,12,999999,999999,999999};//省掉了第0个数

        还记得上面的999999表示的是什么吗？表示的是暂时这两点不连通哟，和上篇文章一样的意思。

       然后，我们讲此时的dis数组中的数称为“预估值”，既然是1号点到其余个点的最短路径，那么就需要先找到一个离1号点最近的点，也就是2号点，那么1号点到2号点的距离有没有可能通过借道其他点的形式变短呢？因为我们两点之间的路径都是正数，也就是说完全没有可能通过借道其他点的方式缩短1到2的距离，因为2已经是距离1最近的点了。所以此时的dis[2] = 1 ,就从预估值，变成了“确定值”，无法也不需要再更改了。

       然后，1到3、4、5、6这几点，有没有可能通过借道2点，然距离变短呢？当然完全是有可能的，，比如1到3，只要1到2和2到3的距离相加小于1到3，那么就可以变短，所以现在就是比较dis[3] 和dis[2] + paths[2][3]的大小就行了， paths[1][2] + paths[2][3] = 1 + 9 = 10，是比dis[3] = 12要小的，所以通过借道2点，我们的dis数组可以更新为如下。

    int[] dis = {0,1,10,4,999999,999999};

    

      这时候，我们需要继续思考，除了确定值外的点，距离1号点最近的是4号点，那么有没有可能通过借道其他点，来缩短1到4的距离呢显然是没有的，因为已经借道过2点了，然后不管是借道3、5、6点都比现在的1到2到4的距离要远，所以dis[4] = 4 现在就变成了确定值。

    int[] dis = {0,1,10,4,999999,999999};

       然后我们需要继续借道4来缩短1到其他点的距离

    int[] dis = {0,1,8,4,17,19};

       此时1到3就变成了1到2到4到3 = 1 + 3 + 4 = 8   1到4 就是1到2到4 = 1 + 3 = 4  1到5 就是1到2到4到5 = 1 + 3 +13 = 17    1到6 就是1到2到4到6 = 1 + 3 +15 = 19

     然后我们需要 从剩下的预估值8、17、19中选出最短的，此时的8已经没法继续缩短了，所以也变成了确定值，理由和上面的相同

    int[] dis = {0,1,8,4,17,19};

    然后从5、6号点钟选出离1号点最近的点，由预估值变成确定值

    int[] dis = {0,1,8,4,13,19};

    然后看1到6能否借助5变短，1到5现在是13  5到6是4，所以1到6就变成了1到5到6 = 13 + 4 = 17

    int[] dis = {0,1,8,4,13,17};

     

     因为到了6之后，已经没有其他的点了，所以现在1到2、3、4、5、6个点的最短距离就确定是上面这个数组中的值了。所以我们就完成了1点到其他各个点的最短距离的计算工作。

    上述的分析过程，其实就是Dijkstra算法的基本思想，让我们来总结一下，他是如何通过哪几步来完成计算的。

         1、将所有顶点分成两部分：已知最短路程的顶点集合P和未知最短路径的顶点集合Q。也就是上面我们的确定值集合和预估值集合。在算法开始的时候，P集合中只有源点一个点。我们这里可以通过一个数组mark来标记哪些点是确定的，哪些点是预估的，确定的点 mark[i] = 1 ，预估的点 mark[i] = 0 。

         2、然后源点到自己的距离我们设为0 ，如果有其他点能之间到源点，则设置为dis[i] = paths[i][s] ，如果不能之间到达就标记为 无穷（999999）。
         3、在集合Q中，选择一个距离源点最近的点，加入到集合P中，然后考察集合Q中的剩余点，能否借助已知最短路径的点，来缩短到源点的距离。
         4、重复第3步，直到集合Q中的元素为0个，算法结束，最终dis数组中的值，就是源点到各个点的最短路径。

     代码编写
     分析完成之后，我们就可以进行代码编写了。
    Dijkstra算法代码如下

   public void dijkstra(int[][] paths,int n){
        int[] dis = new int[n + 1];
        //初始化dis数组
        for (int i = 1; i <= n; i++) {
            dis[i] = paths[1][i];
        }
        //初始化mark数组
        int[] mark = new int[n +1];
        for (int i = 1; i <= n; i++) {
            mark[i] = 0;
        }
        mark[1] = 1;
        while (!isEnd(mark)){
            //先比较所以mark = 0 的值，将最小的那个变成确定值，并且根据这个值来更新dis数组
            int min = 999999;
            int minNum = 1;
            for (int i = 1; i <= n; i++) {
                if (mark[i] == 0 && dis[i] < min){
                    min = dis[i];
                    minNum = i;
                }
            }
            //将这个值变成确定值
            mark[minNum] = 1;
            //并且根据这个确定值来缩小其他dis数组中的值
            for (int i = 1; i <= n; i++) {
                if (dis[i] > dis[minNum] + paths[minNum][i]){
                    dis[i] = dis[minNum] + paths[minNum][i];
                }
            }
        }
        StringBuilder bu = new StringBuilder();
        for (int i = 1; i <= n; i++) {
            bu.append("  "+dis[i]);
        }
        Log.i("hero","---dis == "+bu.toString());
    }
    private boolean isEnd(int[] mark){
        for (int i = 1; i < mark.length; i++) {
            if (mark[i] == 0){
                return false;
            }
        }
        return true;
    }

     isEnd方法，是用来判断估算值集合是否还有数，以便于结束算法的方法.。

   调用代码如下

    public void shortestPath(){
        //初始化城市地图    
        int[][] paths = new int[7][7];//便于理解，多初始化了一个数
        paths[1][1] = 0; paths[1][2] = 1;paths[1][3] = 12;paths[1][4] = 999999;paths[1][5] = 999999;paths[1][6] = 999999;
        paths[2][1] = 999999;paths[2][2] = 0;paths[2][3] = 9;paths[2][4] = 3;paths[2][5] = 999999;paths[2][6] = 999999;
        paths[3][1] = 999999; paths[3][2] = 999999; paths[3][3] = 0;paths[3][4] = 999999;paths[3][5] = 5;paths[3][6] = 999999;
        paths[4][1] = 999999; paths[4][2] = 999999; paths[4][3] = 4;paths[4][4] = 0;paths[4][5] = 13;paths[4][6] = 15;
        paths[5][1] = 999999; paths[5][2] = 999999; paths[5][3] = 999999;paths[5][4] = 999999;paths[5][5] = 0;paths[5][6] = 4;
        paths[6][1] = 999999; paths[6][2] = 999999; paths[6][3] = 999999;paths[6][4] = 999999;paths[6][5] = 999999;paths[6][6] = 0;
        dijkstra(paths,6);
    }

    

     代码运行结果

    从结果可以看出，跟我们的分析结果一模一样。   这个算法的时间复杂度是O（N * N）。

总结

        到这里呢，Dijkstra算法也就学习完毕了，记得尝试自己不看源码完成代码的编写哟。这样才能确定你是否是真的学会了。虽然算法的名字都比较难记，但是他们的思路其实都是很清晰的。下一篇我们就学习一种便于计算最短路径的数据结构：邻接表以及第三种求解最短路径的方法Bellman-Ford算法。

        因个人水平有限，上文难免有错误和遗漏，请大家指正批评

        一同学习，一同进步吧