本课首先介绍了一类新的学习算法——生成学习算法(Generative learning algorithms),并详细地介绍了该算法的一个例子:高斯判别分析(GDA);之后对生成学习算法与之前的判别学习算法进行了简单的对比;最后介绍了一个适合对文本进行分类的算法——朴素贝叶斯算法,并结合该算法介绍了一种常用的平滑技术——Laplace平滑。
判别学习算法
代表:logistic 回归

生成学习算法
生成学习算法与判别学习算法不同,其主要关注的是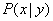


高斯判别分析(GDA)
假设(Assume):
(1)x为n维向量且为连续值
(2) 满足高斯分布
多维高斯分布
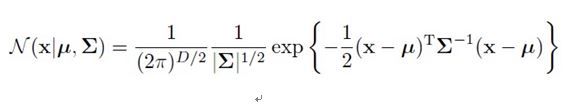
对于多维来说D表示X的维数 , 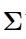


由于y只有0和1两种取值,服从伯努利分布,所以:
生成学习算法是对每一类的特征分别进行建模,那么在这里就应该对y=0和y=1这两类中的特征分别建模。如上式所示。
生成学习算法与判别学习算法同样采用似然判决,但不同的是生成学习算法采用的是Joint Data Likelihood,而判别学习算法采用的是conditional likelihood。具体区别如下:
下面介绍四个参数(

以第二个式子为例进行解释:分子代表只考虑
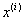


下面我们讨论这个模型的预测操作。给定一个新的x,我们的预测目标是:
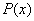
下面是一些推论:
若P(x|y)服从高斯分布,则P(y=1|x)将是一个logistic函数。但是这个结论却不能反向推出,说明P(x|y)服从高斯分布是一个比P(y=1|x)是一个logistic函数更强的假设。推广下去,若 P(x|y)服从泊松分布,P(y=1|x)也将是一个logistic函数。事实上,只要P(x|y)服从指数分布族(EXPfamily),P(y=1|x)就将是一个logistic函数,同样,这个结论不能反向推出。下图就是P(y=1|x)的图像。
上面这些结论有什么用呢?若我们已知训练样本服从或近似服从高斯分布时,我们就可以理所当然的假设P(x|y)服从高斯分布,然后用GDA求解,这往往会带来很好的效果,且相比于logistic回归,它需要更少的数据。若无法确定训练样本的分布,用logistic回归效果往往会更好,但由于其假设很少,相比于生成学习算法,它需呀更多的样本。
朴素贝叶斯算法
在这个算法中,我们假设要设计一个邮件分类器来区分垃圾邮件和非垃圾邮件。其实,朴素贝叶斯算法很适合用于对文本文档进行分类。
下面对朴素贝叶斯算法的基本要素进行讨论:
可以见到,这里的特征向量x是一个元素只能取0和1的n维向量。朴素贝叶斯算法的重要假设是在给定y的时候,
在这里的特征向量是对应词典中的单词的,至于词典需要自己定义。若词典中的单词出现在了邮件里,则特征向量对应的项就要被设为1。
下面对朴素贝叶斯算法的操作进行说明:
以倒数第二个式子为例进行解释。分子代表遍历所有的垃圾邮件,统计其中包含词语j的邮件的数目;分母代表垃圾邮件的总数。
试想一种情况,如果一个词从来有出现在训练样本中(不妨设这个词为sexy,序号为30000),那么不难得到:

那怎么办呢?这个时候Laplace平滑就有用了!
Laplace平滑:
若y有k种取值,则在分母上加k,分子上加1;
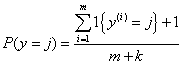
这样就可以避免概率为0或者0/0的情况出现。即在训练样本中只是单纯出现某一种情况,但这不代表其他情况不会发生,这有可能仅仅与训练样本有关,就此看来,若不运用Laplace平滑,就有可能会出现概率为0的错误的情况。









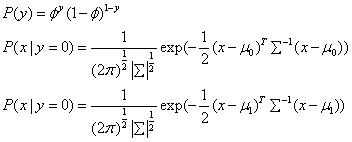






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








