神经网络中的激活函数（activation function）-Sigmoid, ReLu, TanHyperbolic(tanh), softmax, softplus

不管是传统的神经网络模型还是时下热门的深度学习，我们都可以在其中看到激活函数的影子。所谓激活函数，就是在神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。常见的激活函数包括**Sigmoid、TanHyperbolic(tanh)、ReLu、 softplus以及softmax函数。**这些函数有一个共同的特点那就是他们都是非线性的函数。那么我们为什么要在神经网络中引入非线性的激活函数呢？引用https://www.zhihu.com/question/29021768的解释就是：

如果不用激励函数（其实相当于激励函数是f(x) = x），在这种情况下你每一层输出都是上层输入的线性函数，很容易验证，无论你神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，这种情况就是最原始的感知机（Perceptron）了。
正因为上面的原因，我们决定引入非线性函数作为激励函数，这样深层神经网络就有意义了（不再是输入的线性组合，可以逼近任意函数）。最早的想法是sigmoid函数或者tanh函数，输出有界，很容易充当下一层输入（以及一些人的生物解释balabala）。

由此可见，激活函数对神经网络的深层抽象功能有着极其重要的意义，下面根据我在网络上找到的资料，分别对上述激活函数进行说明：
####Sigmoid函数
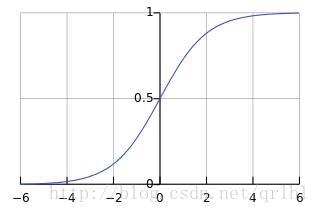
　　Sigmoid函数的表达式为$y=1/(1+e^{-x})$，函数曲线如下图所示：
　　
　　　　　　　　
　　
　　Sigmoid函数是传统神经网络中最常用的激活函数，一度被视为神经网络的核心所在。
　　从数学上来看，Sigmoid函数对中央区的信号增益较大，对两侧区的信号增益小，在信号的特征空间映射上，有很好的效果。
　　从神经科学上来看，中央区酷似神经元的兴奋态，两侧区酷似神经元的抑制态，因而在神经网络学习方面，可以将重点特征推向中央区，将非重点特征推向两侧区。
####TanHyperbolic(tanh)函数
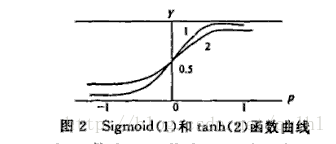
　　TanHyperbolic(tanh)函数又称作双曲正切函数，数学表达式为$y=(e^x-e^{-x})/(e^x+e^{-x})$,其函数曲线与Sigmoid函数相似，tanh函数与Sigmoid函数的函数曲线如下所示：
　　 　　　　
　　
　　在具体应用中，tanh函数相比于Sigmoid函数往往更具有优越性，这主要是因为Sigmoid函数在输入处于[-1,1]之间时，函数值变化敏感，一旦接近或者超出区间就失去敏感性，处于饱和状态，影响神经网络预测的精度值。而tanh的输出和输入能够保持非线性单调上升和下降关系，符合BP网络的梯度求解，容错性好，有界，渐进于0、1，符合人脑神经饱和的规律，但比sigmoid函数延迟了饱和期。

####ReLu函数和softplus函数
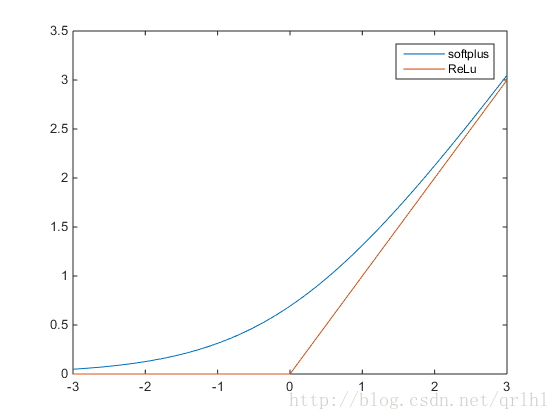
　　ReLu函数的全称为Rectified Linear Units，函数表达式为$y=max(0,x)$，softplus函数的数学表达式为$y=log(1+e^x)$，它们的函数表达式如下：
　　
　　可以看到，softplus可以看作是ReLu的平滑。根据神经科学家的相关研究，softplus和ReLu与脑神经元激活频率函数有神似的地方。也就是说，相比于早期的激活函数，softplus和ReLu更加接近脑神经元的激活模型，而神经网络正是基于脑神经科学发展而来，这两个激活函数的应用促成了神经网络研究的新浪潮。
　　那么softplus和ReLu相比于Sigmoid的优点在哪里呢？引用https://www.zhihu.com/question/29021768的解释就是：

第一，采用sigmoid等函数，算激活函数时（指数运算），计算量大，反向传播求误差梯度时，求导涉及除法，计算量相对大，而采用Relu激活函数，整个过程的计算量节省很多。
第二，对于深层网络，sigmoid函数反向传播时，很容易就会出现梯度消失的情况（在sigmoid接近饱和区时，变换太缓慢，导数趋于0，这种情况会造成信息丢失），从而无法完成深层网络的训练。
第三，Relu会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生（以及一些人的生物解释balabala）。

如果想要了解更多的话，http://www.cnblogs.com/neopenx/p/4453161.html对softplus进行了详细的介绍，这里不再赘述。

####softmax函数
　　我们可以看到，Sigmoid函数实际上就是把数据映射到一个$(0,1)$的空间上，也就是说，Sigmoid函数如果用来分类的话，只能进行二分类，而这里的softmax函数可以看做是Sigmoid函数的一般化，可以进行多分类。softmax函数的函数表达式为：$\sigma (z{)}_j=e^{Z_j}/{\sum }_{k=1}^K{e}^{Z_k}$。从公式中可以看出，就是如果某一个$z_j$大过其他$z$,那这个映射的分量就逼近于1,其他就逼近于0，即用于多分类。也可以理解为将K维向量映射为另外一种K维向量。用通信的术语来讲，如果Sigmoid函数是MISO，Softmax就是MIMO的Sigmoid函数。