最近在做脑电信号分析,在导师的建议下学习了一点经验模式分解(下面简称EMD)的皮毛,期间也是遇到了很多问题,在这里整理出来,一是为了自己备忘,二是为了能尽量帮到有需要的朋友。
一、EMD简介
经验模态分解(Empirical Mode Decomposition,EMD)法是黄锷(N. E. Huang)在美国国家宇航局与其他人于1998年创造性地提出的一种新型自适应信号时频处理方法,特别适用于非线性非平稳信号的分析处理。对经过EMD处理的信号再进行希尔伯特变换,就组成了大名鼎鼎的“希尔伯特—黄变换”(HHT)。由于脑电信号处理很少在EMD之后接上希尔伯特变换,在这里仅介绍EMD的相关基础知识。
EMD其实就是一种对信号进行分解的方法,与傅里叶变换、小波变换的核心思想一致,大家都想将信号分解为各个相互独立的成分的叠加;只不过傅里叶变换以及小波变换都要求要有基函数,而EMD却完全抛开了基函数的束缚,仅仅依据数据自身的时间尺度特征来进行信号分解,具备自适应性。由于无需基函数,EMD几乎可以用于任何类型信号的分解,尤其是在非线性、非平稳信号的分解上具有明显的优势。
EMD的目的是将信号分解为多个本征模函数(IMF)的叠加。IMF必需要满足以下两个条件:
(1)函数在整个时间范围内,局部极值点和过零点的数目必须相等,或最多相差一个;
(2)在任意时刻点,局部最大值的包络(上包络线)和局部最小值的包络(下包络线) 平均必须为零。
为什么IMF一定要满足这两个条件呢?经黄锷等人的研究,满足这两个条件的信号都是单组分的,相当于序列的每一个点只有一个瞬时频率,无其他频率组分叠加。这就为后续的希尔伯特变换铺平了道路,也使得瞬时频率有了意义。
值得一提的是,EMD在数学上还有一些细节无法证明,但是EMD已经在工程领域取得了辉煌的成就,这也是在科学界工程领先理论的一个例子。
二、EMD方法的实现
EMD的实现我决定简单说一下,毕竟我们是使用者而已嘛^_^,有需要的朋友可以自行研究一下。
EMD方法是基于如下假设基础上的:
(1)信号至少有两个极值点,一个极大值和一个极小值;
(2)特征时间尺度通过两个极值点之间的时间定义;
(3)若数据缺乏极值点但有形变点,则可通过数据微分一次或几次获得极值点,然后再通过积分来获得分解结果。
算法流程如下所示:

三、Matlab工具箱安装
在这里我们需要下载两个工具箱,第一个是时频分析工具箱,下载地址为:http://tftb.nongnu.org/;另一个就是EMD工具箱,下载地址为:http://perso.ens-lyon.fr/patrick.flandrin/emd.html。有些同学反映无法下载,现给出百度云地址:https://pan.baidu.com/share/init?surl=-jOdWceZebqnK6kzO2Hhyg,密码 stim。
第一步安装时频分析工具箱,安装这个工具箱是因为EMD工具箱中的一些功能依赖于这个工具箱。安装步骤如下:
(1)解压下载的工具箱,将其复制到matlab的toolbox文件夹下
(2)建立搜索路径,matlab->设置路径->添加并包含子文件夹->找到在toolbox目录下的时频分析工具箱->保存->关闭
第二步为安装EMD工具箱,这个就简单一些了,下载完毕直接运行“install_emd.m”就可以啦。如果在安装之后,Matlab提示“cemdc2_fix.c等文件安装失败”,如果想让其编译成功则可以参考这篇文章:http://forum.vibunion.com/thread-79866-1-1.html,如果嫌麻烦的话,也可以不用修复,不会影响到使用EMD功能的。
四、程序演示
在这里贴上一个小程序作为演示,也可以用来测试工具箱有没有安装好。
fs = 1000;
ts = 1/fs;
t=0:ts:0.3;
z = sin(2*pi*10*t) + sin(2*pi*100*t);
imf=emd(z);
emd_visu(z,t,imf) % EMD专用画图函数
运行完会出现3张图,如下所示:
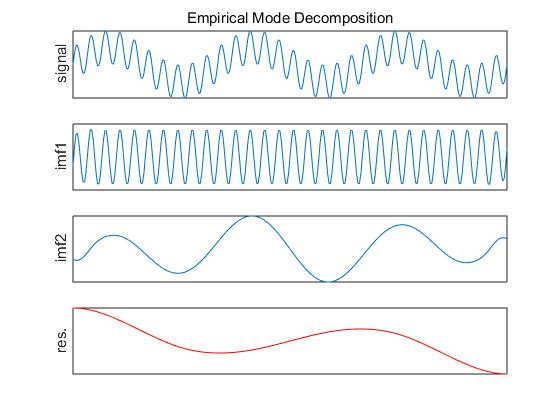
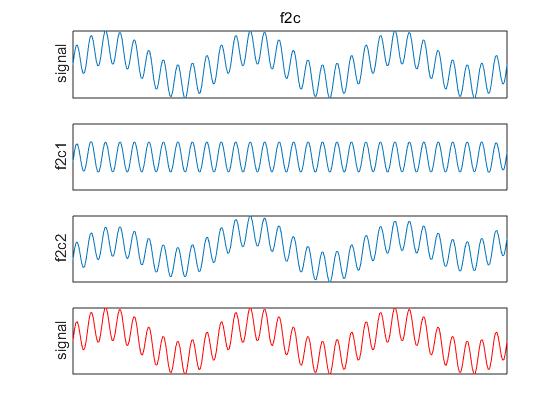










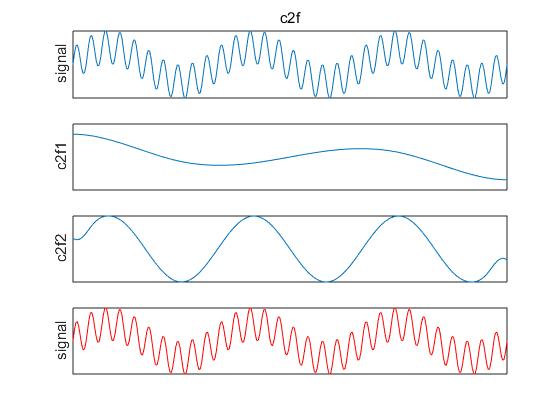














 1173
1173

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








