Logistic回归

最新推荐文章于 2024-07-12 19:06:42 发布

该好好管管

最新推荐文章于 2024-07-12 19:06:42 发布

阅读量59

点赞数

文章标签：机器学习 python

本文链接：https://blog.csdn.net/queerjid/article/details/134789387

版权

在机器学习和统计学中，逻辑回归是一种常用的分类算法。它通过将线性回归模型与逻辑函数结合起来，可以对观测数据进行二分类预测。

线性模型与回归

线性模型

一般形式

$f(x)=w_{1}x_{1}+w_{2}x_{2}+...+w_{d}x_{d}+b$

其中 $x=(x_{1}, x_{2}, ...,x_{d} )$ 是由d维属性描述的样本，其中 $x_{i}$ 是 x 在第 i 个属性上的取值。

向量形式可记为

$f(x)=w^{T}x+b$

其中 $w=(w_{1}, w_{2}, ...,w_{d} )$ 为待求解系数

线性回归目标

给定数据集 $D={(x_{1}, y_{1}), (x_{2}, y_{2}), ..., (x_{m}, y_{m})}$ ,其中 $x_{i}=(x_{i1}, x_{i2}, ..., x_{id}), y_{i}\in R$

线性回归目的是学习一个线性模型以尽可能准确地预测实值输出标记 $f(x)=wx_{i}+b$ 使得 $f(x_{i})\simeq y_{i}$

离散数据处理

离散属性在数据中指的是具有有限取值或者分类的属性，例如性别、血型、职业等。处理离散属性通常需要将其转换为适合模型处理的形式，以下是两个常见的离散属性处理方法：

One-Hot 编码：

对于具有 k 个不同取值的离散属性，可以使用 One-Hot 编码将其转换为 k 维的向量。
对于每个样本，只有对应取值的位置为 1，其他位置为 0。
这种编码方式适用于树模型、神经网络等算法。

标签编码：

对于有序的离散属性，可以使用标签编码将其转换为整数值，从 0 到 k-1。
这种编码方式适用于决策树、随机森林等算法。

最小二乘与参数求解

在线性回归中，我们希望找到最佳的权重 w 和偏置 b 来最小化预测值 f(x) 与真实标记 y 之间的平均误差。为了达到这个目标，我们可以使用最小二乘法来拟合线性模型，即通过最小化预测值和真实标记之间的残差平方和来确定最佳参数。

考虑 $x_{i}$ 是一维数据，设其回归值 $f(x_{i})$ 与实际观察 $y_{i}$ 之间存在的误差 $e_{i}$ ，则学习的目标为

$(w^{*},b^{*})=arg min\sum e_{i}$

$(w^{*},b^{*})=\underset{(w,b)}{argmin}\sum_{i=1}^{m}(f(x_{i})-y_{i})^{2}=\underset{(w,b)}{argmin}\sum_{i=1}^{m}(y_{i}-wx_{i}-b)^{2}$

最小化均方误差

$E_{(w,b)}=\sum_{i=1}^{m}(y_{i}-wx_{i}-b)^{2}$

分别对w和b求导，可得

$\left.\begin{matrix} \frac{\partial E(w,b)}{\partial b}=2(w\sum_{i=1}^{m}-\sum_{i=1}^{m}(y_{i}-b)x_{i})=0 & & \\ & & \\ \frac{\partial E(w,b)}{\partial b}=2(mb-\sum_{i=1}^{m}(y_{i}-wx_{i})=0 & & \end{matrix}\right\}$

得到解析/闭合解

$w=\frac{\sum_{i=1}^{m}(x_{i}-\bar{x})}{\sum_{i=1}^{m}x_{i}^{2}-\frac{1}{m}(\sum_{i=1}^{m}x_{i})^{2}}$ $b=\frac{1}{m}\sum_{i=1}^{m}(y_{i}-wx_{i})$

其中 $\tilde{x}=\frac{1}{m}\sum_{i=1}^{m}x_{i}$

对数线性回归

对数线性回归是一种通过线性模型预测非线性复杂的函数关系的方法。通过对自变量进行对数变换，将原本呈现出指数或幂函数关系的数据转化为线性关系，从而利用线性回归模型进行预测。这使得对数线性回归能够处理那些不适合直接使用线性回归的复杂非线性关系，提供了一种在简单模型下处理复杂函数关系的有效手段。

将线性回归模型y=f(x)=wx+b推广至y=g(f(x))=g(wx+b)，其中g为单调可微函数

例如设 $g(x)=e^{x}$ ，取y的对数，即lny，就可以得到对数线性回归模型：

$y=e^{wx+b}\Leftrightarrow lny=wx+b$

Logistic回归

Logistics 回归是一种分类算法，它用于预测一个事物属于哪个类别。该算法基于逻辑函数和最大似然估计来估计输入变量与输出变量之间的关系。Logistics 回归可以用于二元分类和多元分类，其中二元分类是最常见的应用场景。在二元分类中，算法使用逻辑函数将输入变量映射到一个介于 0 和 1 之间的概率值，这个概率值表示分类为某个类别的概率。

数学原理

Logistics 回归的核心原理是逻辑函数，也称为 sigmoid 函数。sigmoid 函数可以将任何实数值映射到 0 和 1 之间的概率值，其公式如下：

$\sigma(x) = \frac{1}{1 + e^{-x}}$

sigmoid 函数的输入 x 是一个实数，它在函数图像中呈现出 S 形曲线。当 x 趋近于正无穷时，函数的值逐渐趋近于 1；当 x 趋近于负无穷时，函数的值逐渐趋近于 0。通过这种方式，sigmoid 函数将输入变量映射到介于 0 和 1 之间的概率值。

参数估计方法

为了确定逻辑回归模型中的参数，我们需要选择一种合适的估计方法。以下将介绍两种常用的参数估计方法：极大似然估计和梯度下降算法。

极大似然估计

极大似然估计是一种常用的参数估计方法，它通过最大化似然函数来确定模型参数。假设观测数据是独立同分布的，并且每个观测数据点的输出类别服从伯努利分布。我们的目标是找到最优的模型参数，使得观测数据出现的可能性最大化。

对于逻辑回归模型，似然函数可以表示为：

$L(w)=\prod_{i=1}^{n}P(y_{i}|x_{i},w)$

其中，y_i 是观测数据的类别标签，x_i 是输入变量。根据逻辑回归的定义，似然函数可以进一步转换为对数似然函数：

$l(w)=\sum_{i=1}^{n}(y_{i}*log(h_{wx_{i}})+(1-y_{i})*log(h_{wx_{i}}))$

我们的目标是最大化对数似然函数 l(w)，从而找到最优的模型参数 w。通常使用数值优化算法（如梯度下降）来实现这一目标。

梯度下降算法

梯度下降算法是一种常用的优化算法，用于最小化（或最大化）目标函数。对于逻辑回归中的参数估计问题，我们希望最大化对数似然函数 l(w)。

梯度下降算法的基本思想是迭代地更新模型参数，使得每次迭代都能够沿着负梯度方向移动一定步长。在逻辑回归中，我们需要计算对数似然函数关于参数 w 的梯度。

根据求导规则和链式法则，对数似然函数关于参数 w 的梯度可以表示为：

$\bigtriangledown l(w) = \sum_{i=1}^{n} (y_i - h_w(x_i)) * x_i$

其中，∇l(w) 表示对数似然函数关于参数 w 的梯度，y_i 是观测数据的类别标签，x_i 是输入变量。

在每次迭代中，我们根据梯度信息和学习率来更新参数：

其中，α 表示学习率，控制每次迭代的步长大小。

$w := w + \alpha * \bigtriangledown l(w)$

通过迭代更新参数，梯度下降算法可以逐渐接近对数似然函数的最大值，从而找到最优的模型参数 w。

部分数据

代码

读取数据和定义sigmoid函数

import numpy as np
import matplotlib.pyplot as plt

def load_data():
    data = np.loadtxt("D:/python/test.txt", delimiter=' ')
    X = data[:, :3]  # 取前三列作为特征
    y = data[:, 3]  # 取第四列作为标签
    return X, y

def sigmoid(x):
    # sigmoid函数
    return 1.0 / (1 + np.exp(-x))

X, y = load_data()
weights = stoc_grad_ascent(X, y)
plot_decision_boundary(X, y, weights)

随机梯度上升

def stoc_grad_ascent(X, y, max_iter=100):
    # 随机梯度上升算法
    m, n = X.shape
    alpha = 0.01
    weights = np.ones(n)
    for i in range(max_iter):
        for j in range(m):
            # 随机选择一个样本
            rand_index = np.random.randint(0, m)
            h = sigmoid(np.sum(X[rand_index] * weights))
            error = y[rand_index] - h
            weights += alpha * error * X[rand_index]
    return weights

绘制决策边界

def plot_decision_boundary(X, y, weights):
    # 绘制决策边界
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
                         np.arange(y_min, y_max, 0.1))
    Z = sigmoid(np.dot(np.c_[xx.ravel(), yy.ravel(), np.ones(xx.ravel().shape[0])], weights))
    Z = Z.reshape(xx.shape)
    plt.contour(xx, yy, Z, levels=[0.5])
    plt.scatter(X[:, 0], X[:, 1], c=y)
    plt.show()

结果

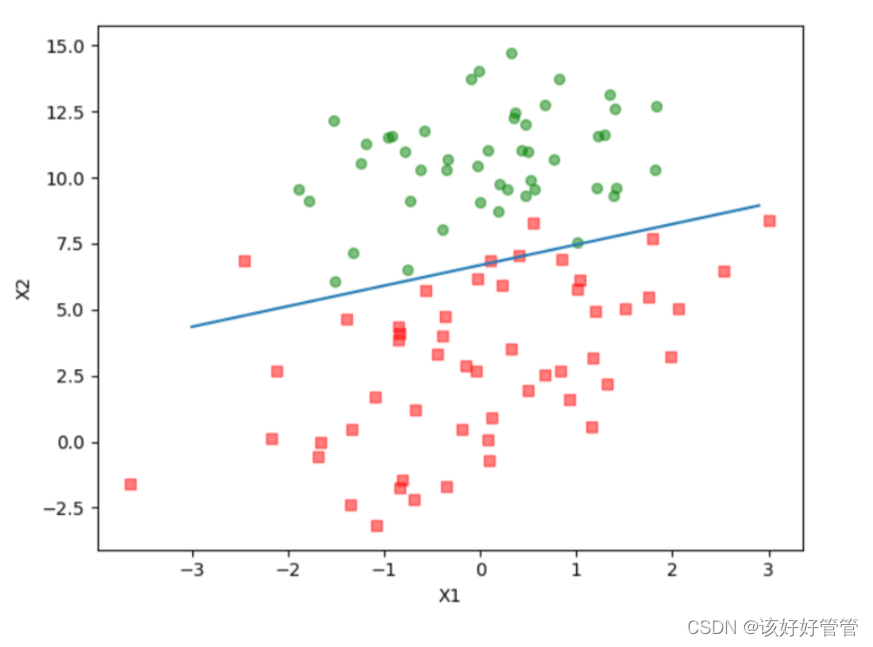
总结

逻辑回归是一种基本的机器学习算法，常用于二分类问题。在本次实验中，实现逻辑回归算法的关键部分，包括sigmoid函数、随机梯度上升算法和决策边界的绘制。首先，定义sigmoid函数，它能将任意实数映射到0到1之间，用于输出概率值。接着，编写随机梯度上升算法来更新模型参数，以便最大化似然函数，使用单个样本来更新模型参数，从而减少计算量并加速收敛。最后，通过绘制决策边界，可以直观地展示分类器在特征空间中的表现。

该好好管管

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
Logistic回归

逻辑回归是一种基本的机器学习算法，常用于二分类问题。在本次实验中，实现逻辑回归算法的关键部分，包括sigmoid函数、随机梯度上升算法和决策边界的绘制。首先，定义sigmoid函数，它能将任意实数映射到0到1之间，用于输出概率值。接着，编写随机梯度上升算法来更新模型参数，以便最大化似然函数，使用单个样本来更新模型参数，从而减少计算量并加速收敛。最后，通过绘制决策边界，可以直观地展示分类器在特征空间中的表现。...+
复制链接

扫一扫