本系列文章面向深度学习研发者,希望通过Image Caption Generation,一个有意思的具体任务,深入浅出地介绍深度学习的知识。本系列文章涉及到很多深度学习流行的模型,如CNN,RNN/LSTM,Attention等。本文为第12篇。
作者:李理
目前就职于环信,即时通讯云平台和全媒体智能客服平台,在环信从事智能客服和智能机器人相关工作,致力于用深度学习来提高智能机器人的性能。相关文章:
李理:从Image Caption Generation理解深度学习(part I)
李理:从Image Caption Generation理解深度学习(part II)
李理:从Image Caption Generation理解深度学习(part III)
李理:自动梯度求解 反向传播算法的另外一种视角
李理:自动梯度求解——cs231n的notes
李理:自动梯度求解——使用自动求导实现多层神经网络
李理:详解卷积神经网络
李理:Theano tutorial和卷积神经网络的Theano实现 Part1
李理:Theano tutorial和卷积神经网络的Theano实现 Part2
李理:卷积神经网络之Batch Normalization的原理及实现
李理:卷积神经网络之Dropout
卷积神经网络的原理已经在《李理:卷积神经网络之Batch Normalization的原理及实现》以及《李理:卷积神经网络之Dropout》二文中详细讲过了,这里我们看怎么实现。
5.1 cell1-2
打开ConvolutionalNetworks.ipynb,运行cell1和2
5.2 cell3 实现最原始的卷积层的forward部分
打开layers.py,实现conv_forward_naive里的缺失代码:
N, C, H, W = x.shape
F, _, HH, WW = w.shape
stride = conv_param['stride']
pad = conv_param['pad']
H_out = 1 + (H + 2 * pad - HH) / stride
W_out = 1 + (W + 2 * pad - WW) / stride
out = np.zeros((N,F,H_out,W_out))
# Pad the input
x_pad = np.zeros((N,C,H+2*pad,W+2*pad))
for n in range(N):
for c in range(C):
x_pad[n,c] = np.pad(x[n,c],(pad,pad),'constant', constant_values=(0,0))
for n in range(N):
for i in range(H_out):
for j in range(W_out):
current_x_matrix = x_pad[n, :, i * stride: i * stride + HH, j * stride:j * stride + WW]
for f in range(F):
current_filter = w[f]
out[n,f,i,j] = np.sum(current_x_matrix*current_filter)
out[n,:,i,j] = out[n,:,i,j]+b我们来逐行来阅读上面的代码
5.2.1 第1行
首先输入x的shape是(N, C, H, W),N是batchSize,C是输入的channel数,H和W是输入的Height和Width
5.2.2 第2行
参数w的shape是(F, C, HH, WW),F是Filter的个数,HH是Filter的Height,WW是Filter的Width
5.2.3 第3-4行
从conv_param里读取stride和pad
5.2.4 第5-6行
计算输出的H_out和W_out
5.2.5 第7行
定义输出的变量out,它的shape是(N, F, H_out, W_out)
5.2.6 第8-11行
对x进行padding,所谓的padding,就是在一个矩阵的四角补充0。
首先我们来熟悉一下numpy.pad这个函数。
In [19]: x=np.array([[1,2],[3,4],[5,6]])
In [20]: x
Out[20]:
array([[1, 2],
[3, 4],
[5, 6]])首先我们定义一个3*2的矩阵
然后给它左上和右下都padding1个0。
In [21]: y=np.pad(x,(1,1),'constant', constant_values=(0,0))
In [22]: y
Out[22]:
array([[0, 0, 0, 0],
[0, 1, 2, 0],
[0, 3, 4, 0],
[0, 5, 6, 0],
[0, 0, 0, 0]])我们看到3*2的矩阵的上下左右都补了一个0。
我们也可以只给左上补0:
In [23]: y=np.pad(x,(1,0),'constant', constant_values=(0,0))
In [24]: y
Out[24]:
array([[0, 0, 0],
[0, 1, 2],
[0, 3, 4],
[0, 5, 6]])了解了pad函数之后,上面的代码就很容易阅读了。对于每一个样本,对于每一个channel,这都是一个二位的数组,我们根据参数pad对它进行padding。
5.2.7 第12-19行
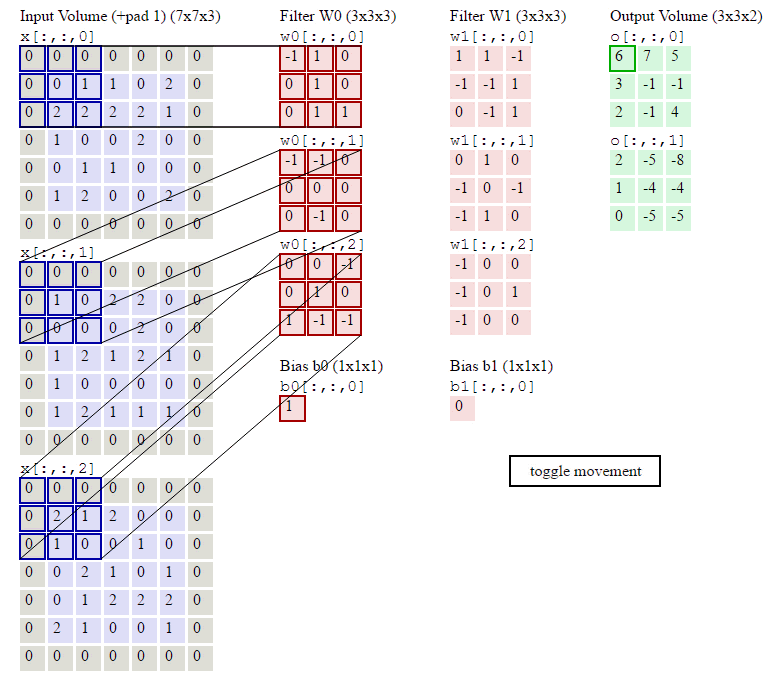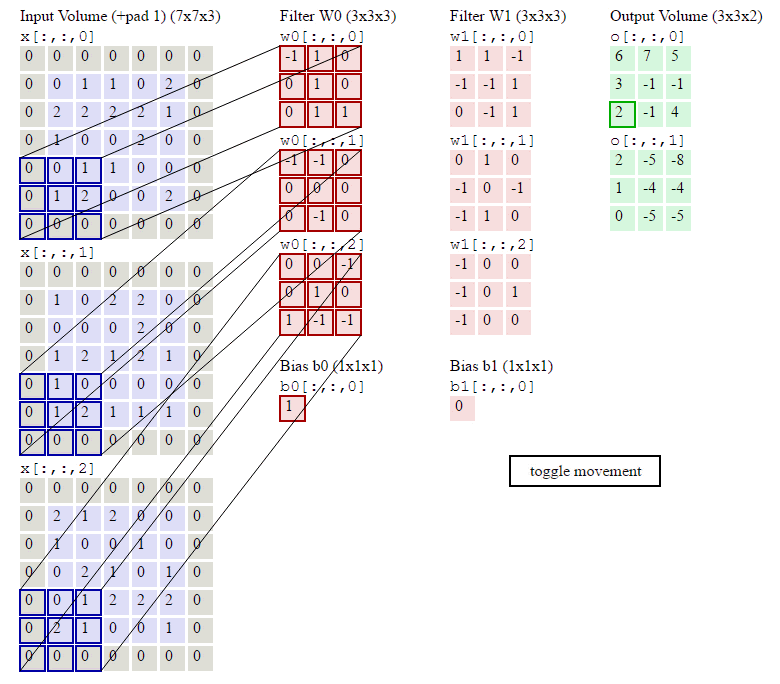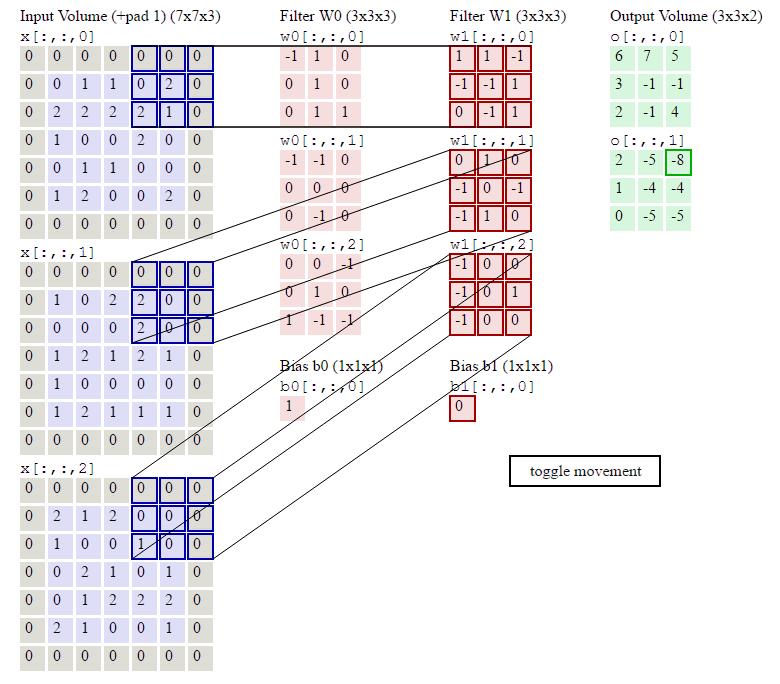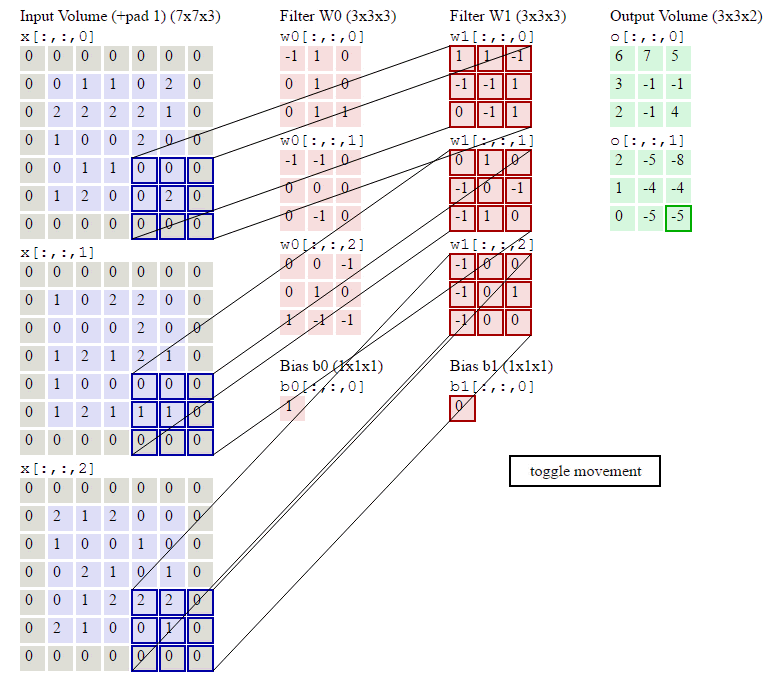
这几行代码就是按照卷积的定义:对于输出的每一个样本(for n in range(N)),对于输出的每一个下标i和j,我们遍历所有F个filter,首先找到要计算的局部感知域:
current_x_matrix = x_pad[n,:, i*stride: i*stride+HH, j*stride:j*stride+WW]这会得到一个(C, HH, WW)的ndarray,也就是下标i和j对应的。
然后我们把这个filter的参数都拿出来:
current_filter = w[f]它也是(C, HH, WW)的ndarray。
然后对应下标乘起来,最后加起来。
如果最简单的实现,我们还应该加上bias
out[n,f,i,j]+=b[f]这也是可以的,但是为了提高运算速度,我们可以把所有filter的bias一次用向量加法实现,也就是上面代码的方式。
其中烦琐的地方就是怎么通过slice得到当前的current_x_matrix。不清楚的地方可以参考下图:
关于上面的4个for循环,其实还有一种等价而且看起来更自然的实现:
for n in range(N):
for f in range(F):
current_filter = w[f]
for i in range(H_out):
for j in range(W_out):
current_x_matrix = x_pad[n, :, i * stride: i * stride + HH, j * stride:j * stride + WW]
out[n, f, i, j] = np.sum(current_x_matrix * current_filter)
out[n, f, i, j] = out[n, f, i, j] + b[f]为什么不用这种方式呢?
首先这种方式bias没有办法写出向量的形式了,其次我觉得最大的问题是切片操作次数太多,对于这种方式,current_x_matrix从x_pad切片的调用次数是N F H_out*W_out。切片会访问不连续的内存,这是会极大影响性能的。
5.3 cell4
通过卷积实现图像处理。
这个cell通过卷积来进行图像处理,实现到灰度图的转化和边缘检测。这一方面可以验证我们之前的算法,另外也可以演示卷积可以提取一些特征。
实现灰度图比较简单,每个像素都是 gray=r∗0.1+b∗0.6+g∗0.3
用一个卷积来实现就是:
w[0, 0, :, :] = [[0, 0, 0], [0, 0.3, 0], [0, 0, 0]]
w[0, 1, :, :] = [[0, 0, 0], [0, 0.6, 0], [0, 0, 0]]
w[0, 2, :, :] = [[0, 0, 0], [0, 0.1, 0], [0, 0, 0]]而下面的filter是一个sobel算子,用来检测水平的边缘:
w[1, 0, :, :] =0
w[1, 1, :, :] =0
w[1, 2, :, :] = [[1, 2, 1], [0, 0, 0], [-1, -2, -1]]感兴趣的读者可以参考 sobel operator
读者可能问了,这么做有什么意义?这个例子想说明的是卷积能够做一些图像处理的事情,而通过数据的驱动,是可以(可能)学习出这样的特征的。而在深度学习之前,很多时候是人工在提取这些特征。以前做图像识别,需要很多这样的算子,需要很多图像处理的技术,而现在就不需要那么多了。
这个cell不需要实现什么代码,直接运行就好了。
5.4 cell5 实现conv_backward_naive
代码如下:
x, w, b, conv_param = cache
stride = conv_param['stride']
pad = conv_param['pad']
N, C, H, W = x.shape
F, _, HH, WW = w.shape
_,_,H_out,W_out = dout.shape
x_pad = np.zeros((N,C,H+2*pad,W+2*pad))
for n in range(N):
for c in range(C):
x_pad[n,c] = np.pad(x[n,c],(pad,pad),'constant', constant_values=(0,0))
db = np.zeros((F))
dw = np.zeros(w.shape)
dx_pad = np.zeros(x_pad.shape)
for n in range(N):
for i in range(H_out):
for j in range(W_out):
current_x_matrix = x_pad[n, :, i * stride: i * stride + HH, j * stride:j * stride + WW]
for f in range(F):
dw[f] = dw[f] + dout[n,f,i,j]* current_x_matrix
dx_pad[n,:, i*stride: i*stride+HH, j*stride:j*stride+WW] += w[f]*dout[n,f,i,j]
db = db + dout[n,:,i,j]
dx = dx_pad[:,:,pad:H+pad,pad:W+pad]代码和forward很像,首先是把cache里的值取出来。由于x_pad没有放到cache里,这里还需要算一遍,当然也可以修改上面的forward,这样避免padding。
然后定义db,dw,dx_pad
最后是和forward完全一样的一个4层for循环,区别是:
#forward
current_x_matrix = x_pad[n, :, i * stride: i * stride + HH, j * stride:j * stride + WW]
out[n,f,i,j] = np.sum(current_x_matrix* w[f])
#backward
dw[f] += dout[n,f,i,j]*current_x_matrix
dx_pad[....]+=dout * w[f]这里的小小技巧就是 z=np.sum(matrix1*matrix2),怎么求dz/dmatrix1。
答案就是matrix2。
所以写出矩阵的形式就是dz/matrix1=matrix2。
我们运行一下这个cell,如果相对误差小于10的-9次方,那么我们的实现就是没有问题的。
5.5 cell6 实现max_pool_forward_naive
N, C, H, W = x.shape
pool_height = pool_param['pool_height']
pool_width = pool_param['pool_width']







 本文由李理撰写,面向深度学习开发者,详细介绍了如何实现三层卷积神经网络和VGG网络。文章涵盖了卷积层的前向传播、反向传播、池化层的实现,以及卷积神经网络的初始化、损失函数、训练数据的拟合等内容。通过实例展示了卷积网络的特征可视化和Spatial Batch Normalization的原理及应用。
本文由李理撰写,面向深度学习开发者,详细介绍了如何实现三层卷积神经网络和VGG网络。文章涵盖了卷积层的前向传播、反向传播、池化层的实现,以及卷积神经网络的初始化、损失函数、训练数据的拟合等内容。通过实例展示了卷积网络的特征可视化和Spatial Batch Normalization的原理及应用。

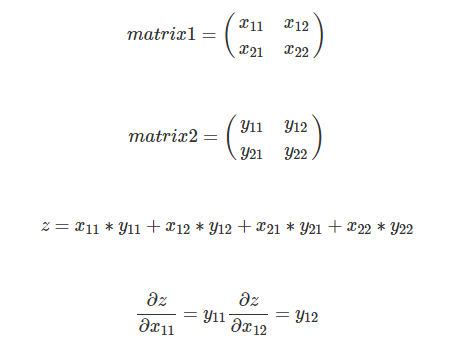
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 339
339

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








