本文深入探讨了谷歌PageRank算法的核心思想，揭示了网页重要性得分的计算方法。通过线性代数，特别是矩阵论，解释了如何通过链接矩阵的特征向量来确定网页的排序。文章指出，对于没有孤立点的网络，链接矩阵总有一个特征值为1的特征向量，这是由于列和为1的性质。此外，针对特征向量不唯一的情况，提出了调整链接矩阵的方案，确保重要性得分的唯一排序。
原文：THE $25,000,000,000∗ EIGENVECTOR THE LINEAR ALGEBRA BEHIND GOOGLE
译者：李乐
一、简介
20世纪90年代，谷歌公司上市并很快成为最具影响力的搜索引擎。谷歌的脱颖而出要归功于它所提供的搜索结果总会把一些“好东西”排在前面，方便用户搜索。与此形成强烈对比的是，如果利用其它搜索引擎，你需要遍历所有搜索结果（包含很多无关信息），从而得到你想获取的信息和资源。谷歌背后的神奇之处就在于PageRank算法。PageRank算法将每个网页的重要性进行量化，从而使其具有可排序性（建立了偏序关系），这样使用户更早地获取到最重要、最相关的网页信息。
我们如果能了解PageRank的计算方法，就可以合理的设计网页，从而获取更多的访问量和点击量。事实也是如此，由于谷歌在搜索方面的主导地位，它的排序系统对于整个互联网的发展和架构起到了重要的影响。这篇文章将解释谷歌计算网页重要性排序的核心思想。这个核心思想又必然地成为了线性代数的华丽的应用。
一个搜索引擎需要做以下三件事情：
- 网络爬虫，获取所有可以公开访问的网页；
- 将所有网页标号，这样可以根据关键词或短语进行快速查找；
- 在数据库中按照网页重要性得分进行排序。这样，当用户进行搜索时，更重要的网页信息就会排在前面。
本文着重分析第三步。在一个互连的网络中，如何定义并且合理量化网页的重要性呢？
二、推导排序公式
2.1 基本思想
在这一部分，我们用“重要性得分”或者“得分”来度量某个网页的在网络中的重要性。显然，重要性得分一定是一个非负实数。我们的核心思想是：给定任意一个网页，它的得分应该和其他网页与其链接的链接数紧密相关（更准确地说是正相关）。这些链接被称为该给定网页的后向链接。可以想象，这样一来，整个网络形成了一种民主投票机制：网页得票数越多（后向链接数越多），它就将被视为越重要。
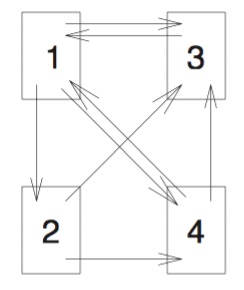
不失一般性地，我们考查某一个包含n个网页的网络，每个网页按序号记为正整数k，1<=k<=n. 如图2.1给出了一个例子，该网络包含四个网页，箭头从1指向4代表网页1有到网页4的链接，其他箭头同理。这样的网在数学上是一个有向图。网页k的得分记为xk，则xk是一个非负实数，并且xj>xk表示网页j的重要性高于网页k。注意到xj=0表示网页j具有最低的重要性得分。
根据我们的核心思想（给定任意一个网页，它的得分应该和其他网页与它链接的链接数成正相关），我们很容易想到用网页k的后向链接数作为网页k的重要性得分。因此，在图2.1所给的例子中，我们有x1=2,x2=1,x3=3,x4=2。排序后可知，网页3最重要，网页1和4并列第二，网页2最不重要。可以想象，网页k的一个后向链接就好比是对于网页k的重要性的一票。
然而，这种简单粗暴的方法忽略了一个对于排序算法来说非常重要的特性，即，给定网页k，来自一个重要性很高的网页的链接会比一个来自不太重要的网页的链接更多地提升网页k的重要性。比如，对于你的个人主页，来自雅虎网页的链接应该比一个来自www.kurtbryan.com网页的链接更大程度上提升你个人主页的重要性。再比如，对于图2.1所示的网络中，网页1和网页4都有两个后向链接：网页1的后向链接来自网页4和看起来比较重要的网页3，网页4的后向链接来自网页2和相对不那么重要的网页1. 由此，我们得到的重要性排序结果应该网页1高于网页4。
为了引入这个重要思想，我们重新定义重要性计算公式。对于网页j，其重要性得分定义为其所有后向链接网页的得分的总和。举个例子，我们重新考虑图2.1所示的网络。网页1的得分为x1=x3+x4。注意到，由于x3和x4又同时依赖于x1，因此这种定义方式看起来是一种自引用的模式。正如在一项选举中，我们不希望某一个候选人仅仅通过给其他人投更多的票数来间接地得到更多的影响力。同样地，我们不希望一个网页仅仅简单地通过链接了更多其他的网页而获取额外的影响力（或者说重要性）。因此我们还需对刚刚的定义稍作修改。假设网页j包含nj个链接，其中一个链接指向网页k，那么这个链接将对网页k的重要性得分贡献xj/nj，而不是xj。由此，我们正式给出重要性得分的定义。对于一个包含n个网页的网络，记Lk ⊂ {1,2,…,n}为具有指向网页k的链接的网页的集合，即Lk为网页k的后向链接网页的集合。那么对于每一个k，我们定义其重要性得分。
其中nj为网页j的出度个数（注意到，nj一定是正整数，因为j属于Lk）。同时我们还假设，自环不会对重要性得分有贡献。也就是说，如果回到我们的比喻中，在这样一个民主投票机制下，我们不允许自投票。
下面，让我们将定义用在图2.1的例子中去。我们很容易得到如下方程组，
接下来，我们开始使用高级的数学工具了—线性代数和矩阵，这将会使整个事情变得简明、优美、清晰，我们定义重要性得分向量x=[x1 x2 x3 x4]T, 我们很容易将上面的方程组写成矩阵的形式Ax=x，其中
熟悉线性代数的读者们会豁然开朗（不熟悉的读者可以回顾：方阵A的特征值λ和特征向量x满足方程Ax=λx，其中x不等于0向量），所有求解的重要性得分向量就是在求解矩阵A的特征值为1的特征向量。我们将这样的矩阵A称为给定网络的链接矩阵。
利用线性代数的知识（计算A-I的行列式，令行列式=0，求解特征根，再求解每一个特征根对应的齐次方程组），我们很容易求解A的特征值为1所对应的特征向量，为任意实数倍的[12 4 9 6]T。由于任意非0实数倍的特征向量还是特征向量，因此我们可以规定将重要性得分向量按照一范数归一化，使分量的和为1. 在这个例子中，x1=12/31=0.386, x2=4/31=0.129, x3=9/31=0.290, x4=6/31=0.194. 注意到这种计算方式和简单的统计后向链接数大不相同。另一个值得注意的方面是，表面上来看，被其他所有网页链接的网页3，出乎意料地，竟不是具有最高重要性得分的网页。为了理解这个现象，我们需要注意到网页3仅仅链接网页1，所以网页3会将所有得票汇集贡献给网页1，这样的一种“间接”投票（或者说影响）使得网页1得到更高的票数（重要性得分）。
然而，在这个例子中，链接矩阵A具有特征值为1的特征向量并不是巧合。在数学上，我们可以严格证明，对于没有孤立点（出度为0的网页节点）的网，其链接矩阵A是一定存在特征值为1的特征向量的。这是由于链接矩阵的列和为1导致的！下面我们来严格证明这个优美的结论。首先我们需要给出马尔科夫链中的一个定义：
定义2.1 一个方阵被称为列随机矩阵当且仅当它的所有元素都为非负且列和（按列加和所有元素）为1。
我们下面来证明定理1.
定理1. 任意列随机矩阵A都有特征值为1的特征向量。
证明：我们要想办法利用到列和为1这一重要性质。注意到，列和为1这一性质用矩阵乘法做形式化可以得到ATe=e,
其中e为全1列向量。这意味着ATx=x有非零解，等价于(AT-I)x=0有非零解，等价于det(AT-I)=0,
等价于det(A-I)=0,
等价于Av=v有非零解，即A有特征值为1的特征向量。证毕。证明过程中如果利用A和AT的具有相同的特征向量（本质上由于行列式按行展开和列展开会具有相同的多项式形式）的这一结论可以简化证明。
在后面的讨论中，我们用V1(A)来表示列随机矩阵A的特征值为1所对应的特征向量所张成的特征空间。
2.2 缺陷
利用式(2.1)来定义给定网页在网络中的重要性得分会存在两个问题：1.网页排序不唯一；2.存在孤立节点。
网页排序不唯一
到目前为止，在我们所做的一切假定和定义下，如果所得到的特征空间的维数为1（即，该特征空间的基的个数为1），那么我们就可以通过归一化找到一个唯一特征向量作为重要性得分向量，这是我们期待的最好情况，图2.1所示的网正是如此。但是，情况并不总是这样。事实上可以证明对于一个强连接的网（任意两个节点在有限步可达），这样的解是唯一的。
我们容易找出网页排序不唯一的例子（链接矩阵的特征值为1所对应的特征空间维数大于1）：
对于这样的链接矩阵A，我们可以计算V1(A)是二维的，它的两个基分别是x=[½,½, 0, 0, 0]T, y=[0, 0, ½, ½, 0]T. 事实并不是只有两种排序那么简单，注意到基间的任意线性组合(lambda x + mu y, lambda,mu属于数域K)还是属于V1(A)（线性空间的封闭性），这样我们就会得到无穷且不可数的排序，而且选择哪一种排序更好并不显然！
更一般地，对于一个无向网W来说，假设它是由r个不连通子网组成，分别记为W1,…,Wr,那么就有dim(V1(A))>=r, 因此就导致有无穷多个特征向量可以成为重要性得分向量。这在直观上也很容易理解：对于这r个互相不连通的子网络来说，各自成体系，要比较来自两个子网络的网页重要性自然很困难。
最为数学的崇尚者，我们需要把这种直观转化成严格的数学证明。假设给定网W有n个网页，包含r个子网络W1,…,Wr. 记ni为Wi所包含的网页个数。因此该网W的链接矩阵就形如一个分块对角结构
其中Ai为Wi的链接矩阵，每个Ai是ni x ni的列随机矩阵，因此每个Ai都有唯一的特征值为1所对应的归一化后的特征向量vi属于Rni，我们将它们拼接在一块可以得到整个矩阵A的特征值为1的一系列特征向量。
很容易证明这些特征向量wi是线性无关的，因此整个特征空间V1(A)至少是由这些特征向量张成的，即V1(A)>=r。
孤立点
另一个问题就是孤立点的存在。如果一个网中存在孤立点，那么这个网所对应的链接矩阵就包含一个或者多个全零列。在这种情况下，我们称A为列次随机，即它的列和都是小于或者等于1的。可以证明这样矩阵的特征值都是小于或等于1的。然而，孤立点的存在不会阻碍我们利用类似的方法对网页进行排序。其中涉及到的一些困难，本文不予论述了。
2.3 对于dim(V1(A))>1的解决方案
对于一个包含几十亿网页的网络来说，为链接矩阵计算一次特征向量需要大量的计算资源。因此我们设计的算法最好可以只产生唯一的网页排名。但是通常情况下，网是不连通的，包含很多的彼此不连通的子网络，根据前面的分析，对于这样的网络链接矩阵的特征值为1的特征向量有无穷多个。这就带来了技术上的矛盾和困难。
下面我们会针对这个问题，引入一个调整方案，从而有效的克服这个困难。这个方案实际上是Perron-Frobenius定理的特例。
改进链接矩阵A
对于包含n个网页的网络，我们定义S是n阶方阵，每个元素都是1/n. 很容易证明S矩阵是列随机矩阵，并且V1(S)是一维的。我们定义矩阵M为
其中0<=m<=1. M矩阵其实就是A和S的加权平均。m是超参，谷歌原始的设置是0.15。对于任意0<=m<=1，M是列随机矩阵，我们还可以证明对于任意0 < m<=1，V1(M)是一维的。由此，M可以替代原来的A来就算无二义性的重要性得分。注意一个极端的情况，当m=1时M=S. 这意味着网络中所有的网页的重要性都相同。
利用M为包含一个孤立点的网络计算重要性得分，我们会得到m/n的得分结果。并且容易得到，对于任意m<1, M是次随机的，因为此时A是次随机的。因此利用式(3.1)对包含孤立点的网计算得分时，可以得到非零的孤立点重要性得分，但是注意到这并不能解决孤立点存在所带来的问题。在接下来的讨论中，我们依然只针对不包含孤立点的网络。
回到计算重要性得分的问题上，方程x=Mx可以写成
其中s是所有元素为1/n的列向量。这是由于我们同时要施加条件x的一范数为1，此时Sx=s是自然成立的。
为什么利用M来计算重要性得分可以解决dim(V1(A))>1而得到唯一的排序结果呢？因为V1(M)是一维的。下面我们来证明这一事实。在我们证明之前，首先看两个例子，感受一下M优于A的地方。
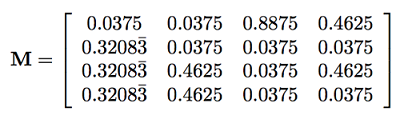
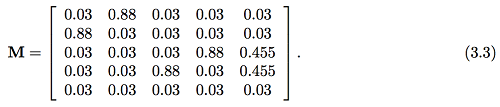
例子一：对于图2.1所示的网，我们可以利用式(3.1)计算出M矩阵（m取0.15）
进而，我们得到x1=0.368, x2=0.142, x3=0.288, x4=0.202. 根据这个得分，我们可以得到同之前相同的排名，但是得分稍有不同。
例子二：类似地，我们考察图2.2给出的网，我们得到
可以计算，V1(M)确实是1维的，而且得分是x1=0.2, x2=0.2, x3=0.285, x4=0.285, x5=0.03. 可以看出，将A取代成M，我们可以对处于不同子网下的网页进行重要性比较了。
看完了两个例子，我们还需要做一个定义。
定义3.1. 我们称矩阵M是正的，当且仅当其所有元素都大于0. 我们稍后可以看到这一重要性质是保证dim(V1(M))=1的关键。
分析M矩阵的性质
根据定理1，我们知道V1(M)是非空的（因为M是随机的）。下面我们将证明V1(M)是1维的。我们首先证明下面两个定理。
定理2. 如果M矩阵是正的并且是列随机的，那么V1(M)中的任何特征向量的所有分量或者都是正的或者都是负的。
证明：我们利用反证法（从中可以体会到数学的美妙之处）。
假设存在x属于V1(M), x的分量符号统一（有的分量大于零；有的分量小于零）。由x=Mx我们可以得到
又由三角不等式且M是正的，得
两边对i求和，我们进一步得到
矛盾产生。假设不成立。证毕。
下面我们不加证明地给出定理3，因为定理3很平凡。
定理3. 给定两个Rm空间中的线性无关向量v和w, m>=2. 那么总存在两个不同时为0的实数s和t，使得x=sv+tw同时具有正负分量。
下面我们真的具备证明dim(V1(M))=1的能力了。2333。。。
证明：我们还是利用反正法。
假设V1(M)空间中存在两个线性无关的特征向量v和w。对于任意不同时为0的实数s和t，非零向量x=sv+tw也在V1(M)空间中。根据定理2，我们知道x的分量或者都是正的、或者都是负的。又根据定理3，我们总可以找到某些s和t使得x的分量既存在正的又存在负的。因此矛盾产生。所以dim(V1(M))=1。
由以上的推理，我们知道，利用M，我们可以得到唯一的特征向量，并且总可以进行归一化，进而得到重要性得分向量。
三、重要性得分的计算方法
在实际应用中，我们并不总需要得到精确的重要性得分，只就意味着，我们不需要利用传统计算特征值的方法来得到重要性得分向量。事实上我们可以利用幂方法来计算M矩阵特征向量的数值解。该方法的思想如下：初始化x0, 开始进行迭代xk=Mx(k-1)… 当k趋于无穷大时，xk就可以作为M的最大特征值对应的特征向量。
为了利用幂方法，我们需要知道，除1以外，M的的其他所有特征值的绝对值都小于1. 我们下面来通过两个定理说明利用幂方法的合理性。
定理4. M是n阶正列随机矩阵，V是Rn的一个子空间，V={v, \sum_j{v_i}=0}. 对于任意v属于V，我们有Mv也属于V，且
其中c满足
证明略。
定理5. 任意正列随机矩阵M都有唯一的正向量q满足Mq=q, 其中q的一范数为1. q可以通过计算
对于任意初始化x0，x0是正向量且满足x0的一范数为1。
证明：
x0是Rn空间的正向量，且满足x0的一范数为1. 则x0=q+v其中v属于V。因此我们有
又因为
其中0<=c<1. 所以，
因此limk Mkx0 = q.
四、总结
我们推导了PageRank的排序公式和算法原理，对于网页排序不唯一的情况，给出了改进方案。最后给出了一种数值结算重要性得分的算法，并说明算法的合理性。从这些严谨的证明推导中，我们可以看到谷歌惊人的价值来源于背后漂亮优美的数学原理，这是数学思想的又一次完美体现！
【6位AI技术大咖分享研发经验 | 本周直播限时特惠 】本期直播（5月13日 周六）邀请来自阿里巴巴、思必驰、第四范式、一点资讯、58集团、PercepIn等在AI领域有着领先技术研究的一批专家，他们将针对人脸识别、卷积神经网络、大规模分布式机器学习系统搭建、推荐系统、自然语言处理及SLAM在机器人领域应用等热点话题进行分享。限时特惠：199元即可听6位技术专家的在线分享，点击报名，加微信小助手 csdncxrs 备注“人工智能”入群。
扫一扫
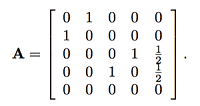
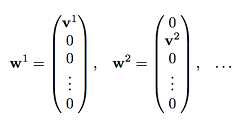
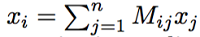
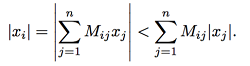
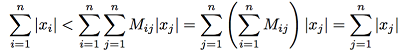
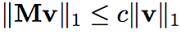
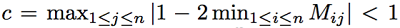
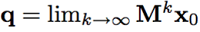
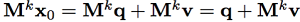
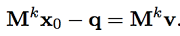
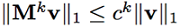
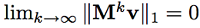
754
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
