一、 图论基础与遍历
1. 图基础结构
首先也是很重要的一点,我们需要知道图就是多叉树的延申
图的抽象结构为如下:(与多叉树很像)
class Vertex {
int id;
vector<Vertex*> neighbors;
};但是一般不使用这种结构存储图,而是使用邻接表和邻接矩阵来实现:


代码实现:
vector<vector<int>> graph;
bool matrix[][];2. 图存储方式
常见的图存储方式有:
邻接表、邻接矩阵、三元组
1.存入邻接表-适合稀疏图(不必开多余空间)
//只存一个点,因为另一个点是邻接表的表头
struct Edge {
int to, weight;
};
vector<Edge> adj[N];
for (int i = 0; i < m; ++i) {
int x, y, z;
cin >> x >> y >> z;
adj[x].push_back({y, z});
}
使用:
for (auto &e : adj[u]) {
int v = e.to;
int w = e.weight;2.邻接矩阵-适合稠密图(不会出现重复存储)
int g[N][N]
while (m -- )
{
int a, b, c;
canf("%d%d%d", &a, &b, &c);
[a][b] = min(g[a][b], c);
}使用:
直接用就行
dist[j] = min(dist[j], dist[t] + g[t][j]);3. 深度优先遍历-dfs
v为图的顶点数,E 为边数。
DFS算法是一一个递归算法,需要借助一个递归工作栈,故它的空间复杂度为O ( V )。
遍历图的过程实质上是对每个顶点查找其邻接点的过程,其耗费的时间取决于所采用结构。
邻接表表示时
查找所有顶点的邻接点所需时间为O ( E ) ,访问顶点的邻接点所花时间为 O ( V ),此时,总的时间复杂度为O ( ∣ V ∣ + ∣ E ∣ ) 。
邻接矩阵表示时
查找每个顶点的邻接点所需时间为O ( V ) ,要查找整个矩阵,故总的时间度为
O ( ∣ V ∣ 2 ) 。
没有最优性,不涉及到最大/最小/最短等,都可以用dfs解决
1.基础框架
我们能体会出来,dfs和回溯其实是非常相似的,下面给出回溯与dfs的对比代码:
回溯:
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}dfs:
void dfs(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本节点所连接的其他节点) {
处理节点;
dfs(图,选择的节点); // 递归
回溯,撤销处理结果
}
}
可以看出dfs和回溯其实代码一模一样,只是处理问题不同,选择列表不一样而已
我将上述dfs框架当作一般框架,另外还发现了一种dfs的框架,代码如下:
void traverse(Graph& graph, int s) {
if (visited[s]) return;
// 经过节点 s,标记为已遍历
visited[s] = true;
// 做选择:标记节点 s 在路径上
onPath[s] = true;
for (int neighbor : graph.neighbors(s)) {
traverse(graph, neighbor);
}
// 撤销选择:节点 s 离开路径
onPath[s] = false;
}可以看出这段代码和一般框架的区别在于我们对节点的处理,一般框架的处理是对每个孩子(邻居)进行处理,而此处是对当前节点进行处理,遇到孩子的时候并没有处理,二者大同小异
具体区别见数据结构与算法-暴力搜索之BFS_双向队列 数据丢失-CSDN博客数据结构与算法-暴力搜索之BFS中的相关分析。
2. 所有可能路径-邻接表使用

此题比较简单,但是能帮助理解如何在图论中使用dfs进行搜索:
由于每次选择列表不同,所有不需要考虑选择列表的去重(剪枝),注意对于这里的选择列表,使用这样的语句进行选择会很清晰,后续可以考虑使用,这里还是使用一般的循环模式
for (int v : graph[s]) {
traverse(graph, v, path);
}根据两种框架给出两种解法,可以体会出两种框架的具体区别:
解法1,每次遍历邻居节点:
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void dfs(vector<vector<int>>& graph,int now){
if(now == graph.size()-1){
res.push_back(path);
return;
}
for(int i = 0;i < graph[now].size();i++){
path.push_back(graph[now][i]);
dfs(graph,graph[now][i]);
path.pop_back();
}
}
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
path.push_back(0);
dfs(graph,0);
return res;
}
};可以看到这里相比一般的回溯多了一行
path.push_back(0);这是因为,我们每次都遍历邻居,那么最开始的起点其实是没有遍历到的,因此要加入path中
解法2,每次遍历当前节点:
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void dfs(vector<vector<int>>& graph,int now){
path.push_back(now);
if(now == graph.size()-1){
res.push_back(path);
//一定要弹出!!!因为我们要对每个节点进行回溯,如果这里return了,就不能自动回溯当前节点了,要手动回溯
path.pop_back();
return;
}
// for(int i = 0;i < graph[now].size();i++){
// path.push_back(graph[now][i]);
// dfs(graph,graph[now][i]);
// path.pop_back();
// }
for(int i = 0;i < graph[now].size();i++){
dfs(graph,graph[now][i]);
}
path.pop_back();
}
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
dfs(graph,0);
return res;
}
};此解法就不需要额外添加起点,因为我们遍历的是当前节点,最开始就会将起点加入,但是仍有注意点,对比解法1:
我们发现将now放入path的操作提前到了终止条件之前,不这样的话当我们遍历到最终节点时,由于已经满足终止,那么最终节点就收集不到了。
其次我们发现在终止条件中额外加了一段回溯,这是因为我们对每个节点进行回溯,最终节点是运行不到相应的回溯语句的,如果这里不加会导致最终节点没有回溯!
3. 名流问题-邻接矩阵的使用(缺少优化方法)

如果我们还是使用邻接表,那么判断名人不认识其他人很简单,只要邻居为空就行,但是判断所有人都认识名人比较难
所以我们考虑使用邻接矩阵。如下图:

我们只需要判断,m[i][i]的行为空,列除了本节点全有值,即是名人
这里给出一个knows()函数来表示认识关系,使用起来和邻接矩阵是一模一样的,按照上面思路,主要不熟悉的在于如何一边进行列操作,一边进行行操作
重点在于,我们处理列的时候将[i][j]变为[j][i]就是处理对应的行上的点了,所以只要[i][j]总是false,[j][i]总是true即可。
具体操作就是,将每一行看做一个人,每一行的元素看做其他人,遍历每一行,再将当前行和其他人的关系都判断一遍,如果和所以人都满足我不认识你你认识我的话,那么这一行代表的人就是名人。
写出代码如下:
int findCelebrity(int n) {
for (int cand = 0; cand < n; cand++) {
int other;
for (other = 0; other < n; other++) {
if (cand == other) continue;
// 保证其他人都认识 cand,且 cand 不认识任何其他人
// 否则 cand 就不可能是名人
if (knows(cand, other) || !knows(other, cand)) {
break;
}
}
//如果能够将一行的每一个元素都遍历一遍不break,说明当前行全满
if (other == n) {
// 找到名人
return cand;
}
}
// 没有一个人符合名人特性
return -1;
}优化解法:
上述解法实际上就是暴力搜索,当然dfs也是暴力搜索,但是这里其实是可以优化的、
如果有两个人同时是名人,那么两条定义就自相矛盾了。
换句话说,只要观察任意两个候选人的关系,我一定能确定其中的一个人不是名人,把他排除。
一共四种情况:

只要情况1,2中可以排除一个人不是名人,3,4中都能说明两个都不是名人
4. 名流问题类题 (缺少使用出入度的方法)

此题和,名流极其类似,但是这里面给出的trust不是一个邻接矩阵,而是只给出相关的人物组合,因此,无法直接使用邻接矩阵的方式判断两个节点的连接关系,所以这里考虑使用哈希表来快速查找
但是注意:哈希表无法用vector<int>或者pair<int,int>当作键值,因为向量是可以改变大小的动态数组,其元素可以是任意类型,很难为所有可能的元素类型和大小提供一个通用的、高效的哈希函数。
所以我们定义了一个名为 hash_pair 的结构,它重载了 operator() 来为 pair<int, int> 提供一个哈希函数。hash_pair 使用了 XOR 操作来组合 pair 的第一个和第二个元素的哈希值。这是一个常见的技巧,用于组合两个哈希值以生成一个新的哈希值。
具体代码和使用如下
重构部分:
struct hash_pair {
template <class T1, class T2>
size_t operator () (const pair<T1, T2>& p) const {
auto hash1 = hash<T1>{}(p.first);
auto hash2 = hash<T2>{}(p.second);
return hash1 ^ hash2;
}
};使用部分:
unordered_set<pair<int, int>, hash_pair> jud_peo;最终按照名流问题,给出了如下代码实现:
class Solution {
public:
int findJudge(int n, vector<vector<int>>& trust) {
unordered_set<pair<int, int>, hash_pair> jud_peo;
for(int i = 0;i <trust.size();i++){
jud_peo.insert({trust[i][0], trust[i][1]});
}
for(int jud = 1;jud <= n;jud++){
int peo = 1;
for(peo;peo <= n;peo++){
if(peo == jud)continue;
if(jud_peo.find({jud,peo}) !=jud_peo.end()|| jud_peo.find({peo,jud}) ==jud_peo.end())break;
}
if(peo == n+1)return jud;
}
return -1;
}
struct hash_pair {
template <class T1, class T2>
size_t operator () (const pair<T1, T2>& p) const {
auto hash1 = hash<T1>{}(p.first);
auto hash2 = hash<T2>{}(p.second);
return hash1 ^ hash2;
}
};
};(不过观察leetcode评论区,发现了很多使用出入度的方案,学到这一块后再在此处添加新的代码)
4. 广度优先遍历-bfs
v为图的顶点数,E 为边数。
BFS是一种借用队列来存储的过程,分层查找,优先考虑距离出发点近的点。无论是在邻接表还是邻接矩阵中存储,都需要借助一个辅助队列,v 个顶点均需入队,最坏的情况下,空间复杂度为O ( v )。
邻接表形式存储时
每个顶点均需搜索一次,时间复杂度T 1 = O ( v ),从一个顶点开始搜索时,开始搜索,访问未被访问过的节点。最坏的情况下,每个顶点至少访问一次,每条边至少访问1次,这是因为在搜索的过程中,若某结点向下搜索时,其子结点都访问过了,这时候就会回退,故时间复 杂度为O ( E ) ,算法总的时间复 度为O ( ∣ V ∣ + ∣ E ∣ ) 。
邻接矩阵存储方式时,查找每个顶点的邻接点所需时间为O ( V ) ,即该节点所在的该行该列。又有v个顶点,故算总的时间复杂度为O ( ∣ V ∣ 2 ) 。
具有最优性,涉及到最大/最小/最短等,需要使用bfs解决
bfs基础结构:
bfs结构,求解最短路:
二、环检测以及拓扑排序
1. 有向图环检测
1. DFS-邻接表

真是蠢猪啊,一个判断条件困了一下午,猪啊!!!!!!!是真的蠢啊,太蠢了,我服了呀
此题算是比较完整的对图进行处理的题目,涉及到邻接表的创建,一般情况dfs的终止条件,visited去重
首先我们观察此题,发现所谓能完成课程就是指课程图中不存在环
在图遍历中,我们都是使用邻接表或者邻接矩阵,这里准备使用dfs,根据dfs的形式,使用邻接矩阵更合适,但是题中并没有给出邻接矩阵,因此,我们需要自己创建邻接矩阵,使用如下代码创建:
vector<vector<int>> buildgraph(int numCourses, vector<vector<int>>& prerequisites){
vector<vector<int>> graph(numCourses);
for(auto edge: prerequisites){
int fis = edge[1],sec = edge[0];
graph[sec].push_back(fis);
}
return graph;
}(这里可以选择使用new进行graph创建,具体区别见c++技巧-CSDN博客-2.1)
如何进行遍历,我们还是使用之前的dfs框架进行遍历,为了方便直接使用在for外部的形式,这里需要注意,由于图中有环,我们需要使用visited进行去重,同时需要检测环的存在
可能我们会想,visited能够去重避免环,那么也可以用来当作判断环位置,但是其实不行
visited是以整个图为维度判断是否重复遍历,path是以路径为维度判断是否有环,而是判断一条路径上是否重复,区别在于后续遍历的处理。两者不能互相替代。
所以我们需要使用一个path存放当前路径,由于不需要输出路径,只需要知道当前走过哪些节点,我们就使用bool当作参数
写出dfs代码如下:
void dfs(vector<vector<int>>& graph,int now){
if(path[now]) nocycle = false;
if(visited[now] || !nocycle)return;
path[now] = true;
visited[now] = true;
for(int i = 0;i < graph[now].size();i++){
// if(!visited[graph[now][i]])
dfs(graph,graph[now][i]);
}
path[now] =false;
}
注意加入visited后终止条件的变化,其实我们不需要在for中过滤,因为就算这个节点遍历过了我们在终止条件中也能将其立即剔除,如果进行过滤相当于不执行if(path),会漏掉关键判定
另外其实不加入visited也可以,因为这里每次都只是将path[now]=true,重复遍历也不会有影响而且遇到环机会return不会一直执行而栈溢出,所以如下代码也可以,不过上述代码可以帮我们理解visited的使用:
(leetcode测试过了,由于没有使用visited去重,导致很多次重复遍历,所以直接超时)
void dfs(vector<vector<int>>& graph,int now){
if(path[now]) nocycle = false;
// if(visited[now] || !nocycle)return;
if(!nocycle)return;
path[now] = true;
// visited[now] = true;
for(int i = 0;i < graph[now].size();i++){
// if(!visited[graph[now][i]])
dfs(graph,graph[now][i]);
}
path[now] =false;
}
注意我们直接使用了path[now]判断,需要在初始化时将path的大小扩充为num,不然会因为访问空指针而报错
最后由于我们要检测环,所以不能只从一个节点开始,要对所有节点都进行检测,完整代码如下:
class Solution {
public:
vector<bool> visited;
vector<bool> path;
bool nocycle = true;
void dfs(vector<vector<int>>& graph,int now){
if(path[now]) nocycle = false;
// if(visited[now] || !nocycle)return;
if(!nocycle)return;
path[now] = true;
// visited[now] = true;
for(int i = 0;i < graph[now].size();i++){
// if(!visited[graph[now][i]])
dfs(graph,graph[now][i]);
}
path[now] =false;
}
vector<vector<int>> buildgraph(int numCourses, vector<vector<int>>& prerequisites){
vector<vector<int>> graph(numCourses);
for(auto edge: prerequisites){
int fis = edge[1],sec = edge[0];
graph[sec].push_back(fis);
}
return graph;
}
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
vector<vector<int>> graph = buildgraph(numCourses,prerequisites);
visited = vector<bool>(numCourses,false);
path = vector<bool>(numCourses,false);
for(int i = 0;i < numCourses;i++){
dfs(graph,i);
}
return nocycle;
}
};
2. BFS-出入度
要想通过bfs解决环检测问题,需要使用出入度进行解题,具体原理如下图:
各节点数字表示入度的值

取走0之后,并将0的邻居的入度都-1: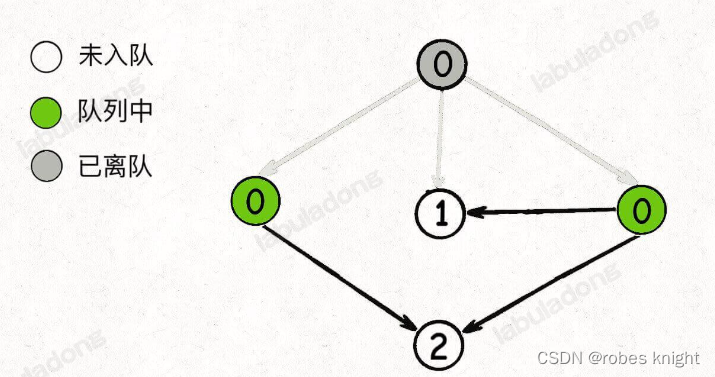
重复操作,取走两个0:
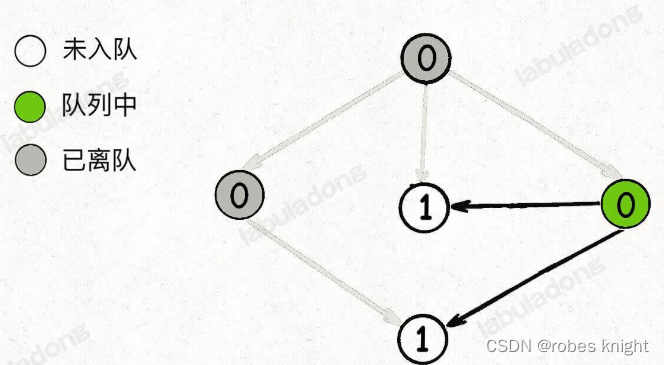
 如果没有环,那么最终所有节点都会按照拓扑排序进行入队
如果没有环,那么最终所有节点都会按照拓扑排序进行入队
如果含有环,会如下图所示,环包含的节点无法入队

所有,将队列里面的元素进行计数,然后与总节点数进行比较就可以知道含不含有环了
完整代码如下:
class Solution {
public:
vector<int> buildindegree(int numCourses, vector<vector<int>>& prerequisites){
vector<int> indegree(numCourses,0);
for(auto i : prerequisites){
int fis = i[1],sec = i[0];
indegree[sec]++;
}
return indegree;
}
vector<vector<int>> buildgraph(int numCourses,vector<vector<int>>& prerequisites){
vector<vector<int>> graph(numCourses);
for(auto i : prerequisites){
int fis = i[1],sec = i[0];
graph[fis].push_back(sec);
}
return graph;
}
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
vector<int> indegree = buildindegree(numCourses,prerequisites);
vector<vector<int>> graph = buildgraph(numCourses,prerequisites);
queue<int> q;
for(int i=0;i < indegree.size();i++){
if(indegree[i]==0)q.push(i);
}
int count = 0;
while(!q.empty()){
int size = q.size();
while(size--){
int cur = q.front();q.pop();
count++;
for(int i:graph[cur]){
indegree[i]--;
if(indegree[i]==0)
q.push(i);
}
}
}
if(count == numCourses)return true;
else return false;
}
};注意这种写法
(int i: indegree) 本题就曾错误的将:
for(int i=0;i < indegree.size();i++){
if(indegree[i]==0)q.push(i);
}写为了:
for(int i :indegree){
if(i==0)q.push(i);
}2. 拓扑排序
1. DFS-邻接表

此题是有向图环检测的plus版,并且引入一个新知识点-拓扑排序
拓扑排序:

图片中拓扑排序的结果有误,
C7->C8->C6应该改为C6->C7->C8
直观地说就是,让你把一幅图「拉平」,而且这个「拉平」的图里面,所有箭头方向都是一致的,比如上图所有箭头都是朝右的。
很显然,如果一幅有向图中存在环,是无法进行拓扑排序的,因为肯定做不到所有箭头方向一致;反过来,如果一幅图是「有向无环图」,那么一定可以进行拓扑排序。
但是我们这道题和拓扑排序有什么关系呢?
其实也不难看出来,如果把课程抽象成节点,课程之间的依赖关系抽象成有向边,那么这幅图的拓扑排序结果就是上课顺序
如何进行拓扑排序?
其实特别简单,将后序遍历的结果进行反转,就是拓扑排序的结果。

后序遍历的这一特点很重要,之所以拓扑排序的基础是后序遍历,是因为一个任务必须等到它依赖的所有任务都完成之后才能开始开始执行
但显然标准的后序遍历结果不满足拓扑排序,而如果把后序遍历结果反转,就是拓扑排序结果了。
这里我会犯糊涂,为什么这样能算后序,我们在dfs函数没有对path进行处理,那么path放哪应该不影响呀:
void dfs(vector<vector<int>>& graph,int now){
// path.push_back(now);
if(onpath[now]){
hascycle = true;
return;
}
if(visited[now])return;
visited[now] = true;
onpath[now] = true;
for(auto i : graph[now])
dfs(graph,i);
path.push_back(now);
onpath[now] = false;
}其实是没有深入思考,虽然dfs中没有处理path,但是我们在递归函数中对path操作是在dfs之后,也就是说其实本质是一样的,都要等最底端的节点操作了,后面节点才能操作
其次,这里涉及到路径,不能重复,则一定要使用visited进去重才行,完整代码如下:
class Solution {
public:
vector<int> path;
vector<bool> visited;
vector<bool> onpath;
bool hascycle = false;
vector<vector<int>> buildgraph(int numCourses,vector<vector<int>>& prerequisites){
vector<vector<int>> graph(numCourses);
for(auto i : prerequisites){
int fis = i[1],sec = i[0];
graph[fis].push_back(sec);
}
return graph;
}
void dfs(vector<vector<int>>& graph,int now){
if(onpath[now]){
hascycle = true;
return;
}
if(visited[now])return;
visited[now] = true;
onpath[now] = true;
for(auto i : graph[now])
dfs(graph,i);
path.push_back(now);
onpath[now] = false;
}
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
vector<int> nores;
vector<vector<int>> graph = buildgraph(numCourses,prerequisites);
onpath = vector<bool>(numCourses,false);
visited = vector<bool>(numCourses,false);
for(int i = 0;i < numCourses;i++)
dfs(graph,i);
if(hascycle)return nores;
reverse(path.begin(),path.end());
return path;
}
};因为是有向图,所以dfs(graph,i) 并不会导致收集重复路径,因为反向收集不了,但还是有点疑问,为什么能保证(?)
2. BFS-出入度
在写过有向图环检测的bfs写法后,再写出拓扑排序的bfs解法并不难,因为其中节点的入队列顺序就是一种拓扑排序!
稍微改一下之后有如下代码:
class Solution {
public:
vector<int> path;
vector<int> visited;
vector<int> buildindegree(int numCourses, vector<vector<int>>& prerequisites){
vector<int> indegree(numCourses,0);
for(auto i : prerequisites){
int fis = i[1],sec = i[0];
indegree[sec]++;
}
return indegree;
}
vector<vector<int>> buildgraph(int numCourses,vector<vector<int>>& prerequisites){
vector<vector<int>> graph(numCourses);
for(auto i : prerequisites){
int fis = i[1],sec = i[0];
graph[fis].push_back(sec);
}
return graph;
}
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
vector<int> indegree = buildindegree(numCourses,prerequisites);
vector<vector<int>> graph = buildgraph(numCourses,prerequisites);
queue<int> q;
vector<int> none;
for(int i=0;i < indegree.size();i++){
if(indegree[i]==0)q.push(i);
}
int count = 0;
while(!q.empty()){
int size = q.size();
while(size--){
int cur = q.front();q.pop();
path.push_back(cur);
count++;
for(int i:graph[cur]){
indegree[i]--;
if(indegree[i]==0)
q.push(i);
}
}
}
if(count != numCourses)return none;
else return path;
}
};注意没有使用visited数组进行去重,因为邻居节点本身已经是筛选后才入队,不需要额外去重
三、并查集
1.并查集基础
1. 动态连通性与并查集
并查集(Union-Find)算法
是一个专门针对「动态连通性」的算法,我之前写过两次,因为这个算法的考察频率高,而且它也是最小生成树算法的前置知识
动态连通性
简单说,动态连通性其实可以抽象成给一幅图连线。比如下面这幅图,总共有 10 个节点,他们互不相连,分别用 0~9 标记:

这里所说的「连通」是一种等价关系,也就是说具有如下三个性质:
1、自反性:节点 p 和 p 是连通的。
2、对称性:如果节点 p 和 q 连通,那么 q 和 p 也连通。
3、传递性:如果节点 p 和 q 连通,q 和 r 连通,那么 p 和 r 也连通。
现在我们的 Union-Find 算法主要需要实现这三个 API:
class UF {
public:
/* 将 p 和 q 连接 */
void union(int p, int q);
/* 判断 p 和 q 是否连通 */
bool connected(int p, int q);
/* 返回图中有多少个连通分量 */
int count();
};函数功能说明:
比如说之前那幅图,0~9 任意两个不同的点都不连通,调用 connected 都会返回 false,连通分量为 10 个。
如果现在调用 union(0, 1),那么 0 和 1 被连通,连通分量降为 9 个。
再调用 union(1, 2),这时 0,1,2 都被连通,调用 connected(0, 2) 也会返回 true,连通分量变为 8 个。

初始化:
怎么用森林来表示连通性呢?我们设定树的每个节点有一个指针指向其父节点,如果是根节点的话,这个指针指向自己。比如说刚才那幅 10 个节点的图,一开始的时候没有相互连通,就是这样:

代码如下:
class UF {
// 记录连通分量
private:
int count;
// 节点 x 的父节点是 parent[x]
int* parent;
public:
/* 构造函数,n 为图的节点总数 */
UF(int n) {
// 一开始互不连通
this->count = n;
// 父节点指针初始指向自己
parent = new int[n];
for (int i = 0; i < n; i++)
parent[i] = i;
}
/* 其他函数 */
};union实现:
操作如下:

代码如下:
class UF {
// 为了节约篇幅,省略上文给出的代码部分...
public:
void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
// 将两棵树合并为一棵
parent[rootP] = rootQ;
// parent[rootQ] = rootP 也一样
count--; // 两个分量合二为一
}
/* 返回某个节点 x 的根节点 */
int find(int x) {
// 根节点的 parent[x] == x
while (parent[x] != x)
x = parent[x];
return x;
}
/* 返回当前的连通分量个数 */
int count() {
return count;
}
};connected实现:
代码如下:
class UF {
private:
// 省略上文给出的代码部分...
public:
bool connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
};2. 平衡性优化-union优化
分析union和connected的时间复杂度,我们发现,主要 API connected和 union 中的复杂度都是 find 函数造成的,所以说它们的复杂度和 find 一样。
find 主要功能就是从某个节点向上遍历到树根,其时间复杂度就是树的高度。我们可能习惯性地认为树的高度就是 logN,但这并不一定。logN 的高度只存在于平衡二叉树,对于一般的树可能出现极端不平衡的情况,使得「树」几乎退化成「链表」,树的高度最坏情况下可能变成 N。
图论解决的都是诸如社交网络这样数据规模巨大的问题,对于 union 和 connected 的调用非常频繁,每次调用需要线性时间完全不可忍受。
关键在于 union 过程,我们一开始就是简单粗暴的把 p 所在的树接到 q 所在的树的根节点下面,那么这里就可能出现「头重脚轻」的不平衡状况,比如下面这种局面:

长此以往,树可能生长得很不平衡。我们其实是希望,小一些的树接到大一些的树下面,这样就能避免头重脚轻,更平衡一些。解决方法是额外使用一个 size 数组,记录每棵树包含的节点数,我们不妨称为「重量」:
class UF {
private:
int count;
int* parent;
// 新增一个数组记录树的“重量”
int* size;
public:
UF(int n) {
this->count = n;
parent = new int[n];
// 最初每棵树只有一个节点
// 重量应该初始化 1
size = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
}
/* 其他函数 */
};比如说 size[3] = 5 表示,以节点 3 为根的那棵树,总共有 5 个节点。这样我们可以修改一下 union 方法:
class UF {
private:
// 为了节约篇幅,省略上文给出的代码部分...
public:
void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
// 小树接到大树下面,较平衡
if (size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
count--;
}
};
这样,通过比较树的重量,就可以保证树的生长相对平衡,树的高度大致在 logN 这个数量级,极大提升执行效率。
此时,find , union , connected 的时间复杂度都下降为 O(logN),即便数据规模上亿,所需时间也非常少。
3. 路径压缩-find优化
其实我们并不在乎每棵树的结构长什么样,只在乎根节点。
因为无论树长啥样,树上的每个节点的根节点都是相同的,所以能不能进一步压缩每棵树的高度,使树高始终保持为常数?

这样每个节点的父节点就是整棵树的根节点,find 就能以 O(1) 的时间找到某一节点的根节点,相应的,connected 和 union 复杂度都下降为 O(1)。
要做到这一点主要是修改 find 函数逻辑,非常简单,但你可能会看到两种不同的写法。
方法1:
class UF {
// 为了节约篇幅,省略上文给出的代码部分...
private:
int find(int x) {
while (parent[x] != x) {
// 这行代码进行路径压缩
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
};每次使得当前x指向父节点的父节点,这样会将一些节点向上移,然后缩短树的长度

压缩结束为:

方法二:
class UF {
// 为了节约篇幅,省略上文给出的代码部分...
// 第二种路径压缩的 find 方法
public:
int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
};其迭代写法如下(便于理解):
int find(int x) {
// 先找到根节点
int root = x;
while (parent[root] != root) {
root = parent[root];
}
// 然后把 x 到根节点之间的所有节点直接接到根节点下面
int old_parent = parent[x];
while (x != root) {
parent[x] = root;
x = old_parent;
old_parent = parent[old_parent];
}
return root;
}最终效果:

4. 并查集框架-优化后
class UF {
private:
// 连通分量个数
int count;
// 存储每个节点的父节点
int *parent;
public:
// n 为图中节点的个数
UF(int n) {
this->count = n;
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
// 将节点 p 和节点 q 连通
void union_(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
parent[rootQ] = rootP;
// 两个连通分量合并成一个连通分量
count--;
}
// 判断节点 p 和节点 q 是否连通
bool connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
// 返回图中的连通分量个数
int count_() {
return count;
}
};2.并查集适用问题
1. 寻找图中是否存在路径

直接使用并查集类,将所有能链接的都链接起来,然后检测source和destinnation是否connection
代码如下:
class uf{
private:
int count;
int* parent;
public:
uf(int n){
this->count = n;
parent = new int [n];
for(int i = 0;i < n;i++)
parent[i] = i;
}
void Union(int p,int q){
int rootP = find(p);
int rootQ = find(q);
if(rootP == rootQ)
return;
parent[rootP] = rootQ;
count--;
}
int find(int x){
if(parent[x]!=x)
parent[x] = find(parent[x]);
return parent[x];
}
int connect(int p,int q){
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
};
class Solution {
public:
bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
uf uf(n);
for(auto s : edges)
uf.Union(s[0],s[1]);
return uf.connect(source,destination);
}
};2. 并查集解决DFS问题-(缺)
后续补充
3. 等式方程判断

动.态连通性其实就是一种等价关系,具有「自反性」「传递性」和「对称性」,其实 == 关系也是一种等价关系,而!=就表示未连通,具有这些性质。所以这个问题用 Union-Find 算法就很自然。
核心思想是,将 equations 中的算式根据 == 和 != 分成两部分,先处理 == 算式,使得他们通过相等关系各自勾结成门派(连通分量);然后处理 != 算式,检查不等关系是否破坏了相等关系的连通性。
代码实现:
class uf{
private:
int count;
int* parent;
public:
uf(int n){
this->count = n;
parent = new int [n];
for(int i = 0;i < n;i++)
parent[i] = i;
}
void Union(int p,int q){
int rootP = find(p);
int rootQ = find(q);
if(rootP == rootQ)
return;
parent[rootP] = rootQ;
count--;
}
int find(int x){
if(parent[x]!=x)
parent[x] = find(parent[x]);
return parent[x];
}
int connect(int p,int q){
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
};
class Solution {
public:
bool equationsPossible(vector<string>& equations) {
uf uf(26);
for(auto s : equations){
if(s[1]=='=')
uf.Union(s[0]-'a',s[3]-'a');
}
for(auto s : equations){
if(s[1]=='!'){
if(uf.connect(s[0]-'a',s[3]-'a'))return false;
}
}
return true;
}
};
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








