动态规划-子序列问题（线性dp）

robes knight

已于 2024-05-15 20:41:20 修改

阅读量1.1k

点赞数 13

分类专栏：数据结构与算法文章标签：动态规划算法

于 2023-11-27 22:38:32 首次发布

本文链接：https://blog.csdn.net/qwertyasdfghh/article/details/134199571

版权

数据结构与算法专栏收录该内容

19 篇文章 0 订阅

订阅专栏

一、子序列子串问题总结:

1.dp定义

一般有两种dp定义

1)dp[i]表示[0-i]对应得到的结果，且结果以nums[i]结尾（下文称结尾定义法）

2)dp[i]表示[0,i]得到的结果，且不要求包含i的结果（下文称区间定义法）

序列系列的题可以分为有序序列、连续、相等序列、总和序列等。

1:要求有序（递增或递减）或连续往往都是结尾定义法

2:相等且不连续往往都是区间定义法

因为前者如果失序或者不连续了需要从头再来，而后者可以在之前的保存的状态上接着操作

=========================重要！！！！！！！！！========================

(注意:为例初始化方便,一般的dp[i][j]0对应nums[i-1]和nums2[j-1])

值得注意的一点：

我们定义dp的时候就会定义有多少状态需要计算，这里需要注意留一份位置，也就是dp[0]，我们需要一种情况来表示没有进行任何选择或者是没有选择空间，这种情况就是dp[0] ，也就是定义的时候一般定义空间大小为n+1

同时，后面进行遍历的时候，需要从1遍历到n而不是0到n-1

2.转移方程

转移方程的确立本质上就是分情况讨论

1：对于当前nums[i]，选或者不选(必选dp[i-1])

2：对于前nums[0,i-1]的dp[0,i-1]枚举选哪个（必选nums[i]）

我们写状态转移的本质就是，如果根据现有的条件(nums[i]和dp[i-1])写出dp[i](或者dp[i][j])

对于单序列：

对于要求连续的问题，一般使用以结尾定义法定义dp，由于定义，nums[i]是必选的，那么我们就要枚举选择dp[0,i-1],但是又要求连续，只能选择dp[i-1]，因此就是选dp[i-1]或者不选

对于要求顺序的问题，一般使用以结尾定义法定义dp，由于定义，nums[i]是必选的，那么我们就要枚举选择dp[0,i-1]

（上面两种情况如果用区间定义法，转移方程是很难写不出来的）

对于其他类型，一般以区间定义法为主，dp[i-1]必选，我们要决定的是nums[i]选或者不选

（其他类型用结尾定义法也可以做，但是由于要枚举前i-1个dp，时间复杂度是o2（单序列），会超时）

对于双序列问题：

整体和单序列类似，以编辑距离为母题

一般会对比nums1[i]和nums2[j],通常相同时,我们考虑dp[i-1][j-1]转移到dp[i][j],而不同时考虑dp[i-1][j-1],dp[i][j-1],dp[i-1][j]如何转移到dp[i][j],例如下图:

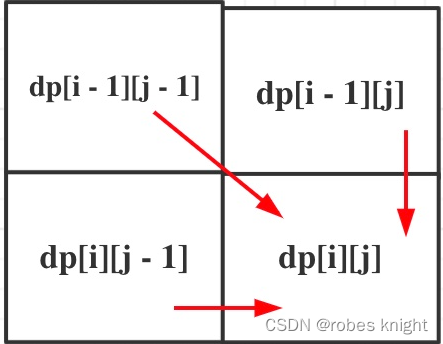
3.初始化

这一步需要在转移方程之后写,因为我们要确定转移方程可行,才能开始初始化,首先我们要画出如下的dp数组(此处针对双序列,单序列一般只初始化dp[0])

根据dp数组定义在橙色位置填上初始值,然后可以使用转移方程检查一下合理

图中红字很重要

4.遍历顺序

从初始化开始往后遍历即可,类似下图:

5.检查dp数组

觉得有问题,就把dp数组打印出来, 看和画的一样不

二、单序列问题

1. 最长递增子序列

题目链接：300. 最长递增子序列 - 力扣（LeetCode）

1：首先确定如何定义dp数组

我们使用子序列一般定义方式，定义dp[i]为以nums[i]结尾的子序列的解（也即是这一部分的严格递增子序列最大长度） ,注意：这里特别还有一点，求得的最大子序列必须包含nums[i]，为了和之后的转移方程进行匹配

2：确定转移方程

转移方程的确定一定要根据数学归纳法来求解，因为我们要求dp[nums.size()],所以我们假设知道dp[0,.....,nums.size()-1]，直接理解不是很清晰，作图如下：

为了推导到更一般的情况，我们假设前面已知的为dp[i]，当前需要求得的时dp[j]，因为每一个子序列的解必须包含nums[i]，所以如果当前的nums[j]比前面某一个nums[i]大的话，就可以直接接在后面，那么dp[j]的解至少也是dp[i]+1。

最后想要求得dp[j]实际上比dp[i]大多少，我们只需要比较所有比nums[j]小的nums[i]，选取最大的dp[i]进行+1即可

因此转移方程为：

for(int i = 0;i < j; i++)
    if(nums[j] > nums[i])
        dp[j] = max(dp[j],dp[i]+1)

3:确定初始状态

由于dp[i]表示nums[i]结尾且包含nums[i]的解，所有解的长度至少为1，也就是nums[i]本身，因此我们需要对dp[i]初始化为1；

4：遍历顺序

由于我们求解dp[j]时会用到dp[0,..,j-1]所有我们顺序遍历即可

5：打印dp

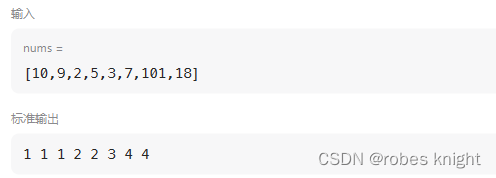
完整代码如下：

dp数组法

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n,1);
        dp[0] = 1;
        for(int i = 0;i < nums.size();i++)
            for(int j = 0;j < i;j++){
                if(nums[i] > nums[j]){
                    dp[i] = max(dp[i],dp[j]+1);
                }
            }
        int res=0;
        for(int i : dp){
            res = max(res,i);
        }
        return  res;
    }
};

时间复杂度O(n^2)

此题有一种更加巧妙的解法,可以进一步降低时间复杂度:

二分法优化

    int lengthOfLIS(vector<int>& nums) {
        int piles = 0;    // 牌堆数初始化为 0
        vector<int> top(nums.size());   // 牌堆数组 top
        
        for (int i = 0; i < nums.size(); i++) {
            int poker = nums[i];    // 要处理的扑克牌

            /***** 搜索左侧边界的二分查找 *****/
            int left = 0, right = piles;    // 搜索区间为 [left, right)
            while (left < right) {
                int mid = (left + right) / 2;    // 防溢出
                if (top[mid] > poker) {
                    right = mid;
                } else if (top[mid] < poker) {
                    left = mid + 1;
                } else {
                    right = mid;
                }
            }
            /*********************************/

            // 没找到合适的牌堆，新建一堆
            if (left == piles) piles++;
            // 把这张牌放到牌堆顶
            top[left] = poker;
        }
        // 牌堆数就是 LIS 长度
        return piles;
    }

时间复杂度O(n*log2n)

2. 俄罗斯套娃信封

此题为最长递增递增子序列的二维形式,本质还是找形状递增的最长子信封,主要问题在于,我们如何将形状引入进行比较

此处处理十分的巧妙:

先对宽度 w 进行升序排序，如果遇到 w 相同的情况，则按照高度 h 降序排序；之后把所有的 h 作为一个数组，在这个数组上计算 LIS 的长度就是答案。

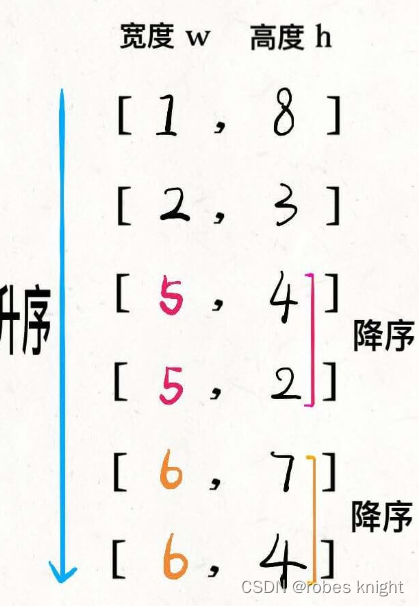
为什么是这样呢,因为我们先使得宽度排好序,然后对高度求最长递增子序列,就能得到递增的信封,但是考虑到相同宽度不能相互装,也即是同一宽度我们只能使用一个信封,所以我们选择将同一宽度下的高度进行降序,这样在降序中,只有可能取其中之一(因为我们找的是升序排列)

lambda

这里引入lambda表达式进行排序:

c++ lambda 看这篇就够了！（有点详细）_c++ 运行时构建 lamda-CSDN博客

        sort(envelopes.begin(), envelopes.end(), 
            [](const vector<int> a, const vector<int>& b) {
                // return a[0] == b[0] ? b[1] - a[1] : a[0] - b[0];
                if (a[0] != b[0]) {
                    return a[0] < b[0]; // 按宽度升序排序
                } else {
                    return a[1] > b[1]; // 如果宽度相同，按高度升序排序
                }
                });

然后我们对排好序的信封的高进行最长递增子序列求解,直接调用函数即可

dp数组法:

    int maxseq(vector<int>& seq) {
        int size = seq.size(),res= 0;
        vector<int> dp(size,1);
        dp[0] = 1;
        for(int i = 0;i< size;i++){
            for(int j = 0;j< i;j++){
                if(seq[i] > seq[j]){
                    dp[i] = max(dp[i],dp[j]+1);
                }
            }
            res = max(dp[i],res);   
        }
        return res;
    }

二分优化:

    int lengthOfLIS(vector<int>& nums) {
        int piles = 0;    // 牌堆数初始化为 0
        vector<int> top(nums.size());   // 牌堆数组 top
        
        for (int i = 0; i < nums.size(); i++) {
            int poker = nums[i];    // 要处理的扑克牌

            /***** 搜索左侧边界的二分查找 *****/
            int left = 0, right = piles;    // 搜索区间为 [left, right)
            while (left < right) {
                int mid = (left + right) / 2;    // 防溢出
                if (top[mid] > poker) {
                    right = mid;
                } else if (top[mid] < poker) {
                    left = mid + 1;
                } else {
                    right = mid;
                }
            }
            /*********************************/

            // 没找到合适的牌堆，新建一堆
            if (left == piles) piles++;
            // 把这张牌放到牌堆顶
            top[left] = poker;
        }
        // 牌堆数就是 LIS 长度
        return piles;
    }

值得一提的是,本题由于一些恶心的例子,只有使用二分法求解递增子序列才不会超时

完整代码如下:

class Solution {
public:
//超时
    int maxseq(vector<int>& seq) {
        int size = seq.size(),res= 0;
        vector<int> dp(size,1);
        dp[0] = 1;
        for(int i = 0;i< size;i++){
            for(int j = 0;j< i;j++){
                if(seq[i] > seq[j]){
                    dp[i] = max(dp[i],dp[j]+1);
                }
            }
            res = max(dp[i],res);   
        }
        return res;
    }
//不超时
    int lengthOfLIS(vector<int>& nums) {
        int piles = 0;    // 牌堆数初始化为 0
        vector<int> top(nums.size());   // 牌堆数组 top
        
        for (int i = 0; i < nums.size(); i++) {
            int poker = nums[i];    // 要处理的扑克牌

            /***** 搜索左侧边界的二分查找 *****/
            int left = 0, right = piles;    // 搜索区间为 [left, right)
            while (left < right) {
                int mid = (left + right) / 2;    // 防溢出
                if (top[mid] > poker) {
                    right = mid;
                } else if (top[mid] < poker) {
                    left = mid + 1;
                } else {
                    right = mid;
                }
            }
            /*********************************/

            // 没找到合适的牌堆，新建一堆
            if (left == piles) piles++;
            // 把这张牌放到牌堆顶
            top[left] = poker;
        }
        // 牌堆数就是 LIS 长度
        return piles;
    }

    int maxEnvelopes(vector<vector<int>>& envelopes) {
        int n = envelopes.size();
        // 按宽度升序排列，如果宽度一样，则按高度降序排列
        sort(envelopes.begin(), envelopes.end(), 
            [](const vector<int> a, const vector<int>& b) {
                // return a[0] == b[0] ? b[1] - a[1] : a[0] - b[0];
                if (a[0] != b[0]) {
                    return a[0] < b[0]; // 按宽度升序排序
                } else {
                    return a[1] > b[1]; // 如果宽度相同，按高度升序排序
                }
                });

        // 对高度数组寻找 LIS
        vector<int> height(n);
        for (int i = 0; i < n; i++){
            height[i] = envelopes[i][1];
            // cout<<envelopes[i][0]<<envelopes[i][1]<<endl;
        }
        return lengthOfLIS(height);
    }
};

3. 最长连续递增子序列

题目链接:674. 最长连续递增序列 - 力扣（LeetCode）

因为要求连续，所以我们对在上一题基础上，只对相邻两个值进行判断，转移方程如下：

            if(nums[i] > nums[i-1])
                dp[i] = dp[i-1]+1;
            res = max(res,dp[i]);

完整代码如下:

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        if(nums.size()==0)return 0;
        int res =1;
        vector<int> dp(nums.size(),1);
        for(int i = 1;i < nums.size() ;i++){
            if(nums[i] > nums[i-1])
                dp[i] = dp[i-1]+1;
            res = max(res,dp[i]);//上一题的优化部分，边求解边求最大值，省时间
        }
        
        return res;
    }
};

4. 最大子序列和--转移方程涉及对以nums[i]结尾的理解

dp定义:

dp[i]：包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]。

转移方程:

依据题意,我们会很自然的想到,要通过nums[i]是否让子序列继续保持增长来作为判断条件,但事实上这样无法判断,因为当nums[i]+dp[i-1] < dp[i-1]时,也可能保留原序列继续扩展,如图:

因此我们重新思考判断条件,首先我们要明确,得到的子序列要以nums[i]结尾,所以必须以nums[i]为基准进行参考,也就是先思考一定要留下nums[i],再思考是否留下前面的子序列,应该是考虑dp[i-1]是否大于0,dp[i-1]大于0的话,nums[i]为结尾的子序列可以增加,那么可以将nums[i]接到前面子序列的后面,如果dp[i-1]小于0,那么 ums[i]为结尾的子序列加上dp[i-1]就会减少,所以我们直接保留nums[i]即可,因此代码如下图:

            if(dp[i-1] < 0)
            dp[i] = nums[i];
            else
            dp[i] = dp[i-1] + nums[i];

简化一下:

            dp[i] = max(dp[i-1]+nums[i],nums[i]);

初始化

因为dp[i]由dp[i-1]决定,那么dp[0]就是最开始的初始状态.
根据dp[i]的定义，很明显dp[0]应为nums[0]即dp[0] = nums[0]

确定遍历顺序

递推公式中dp[i]依赖于dp[i - 1]的状态，需要从前向后遍历。

完整代码如下:

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size(),res = INT_MIN;
        vector<int> dp(nums);
        res = dp[0];// 因为循环是从1开始，遍历不到0，所以此处直接将nums【0】赋给res，模拟一个第一轮
        for(int i = 1;i < n;i++){
            // if(dp[i-1] < 0)
            // dp[i] = nums[i];
            // else
            // dp[i] = dp[i-1] + nums[i];
            dp[i] = max(dp[i-1]+nums[i],nums[i]);
            res= max(dp[i],res);
        }
        return res;
    }   
};

注意此处,res不是从0开始进行遍历的,那么会漏掉对dp[0]的比较,所以我们需要将dp[0]初始化为res的初值(为了不再后面再进行一层循环来求解res的最大值)

由于这里dp[i]只和dp[i-1]有关,所以我们可以使用状态压缩,使用两个变量保持dp[i]和dp[i-1]而不使用dp数组,这样空间复杂度会进一步降低

//状态压缩
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size(),res = INT_MIN;
        int dp_0=nums[0],dp_1;
        res = nums[0];
        for(int i = 1;i < n;i++){
            dp_1 = max(dp_0+nums[i],nums[i]);
            dp_0 = dp_1;
            res= max(dp_1,res);
        }
        return res;
    }   
};

此题还可以使用双指针进行解答,代码如下,具体解释减数组双指针一节:

// 双指针法
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        // if(nums.size()==1)return nums[0];
        int l=0,r=0;
        int sum=0,maxsum=INT_MIN;
        cout<<maxsum;
        while(r<nums.size()){
            sum+=nums[r];
            maxsum = max(maxsum,sum);
            while(sum<0){
                sum-=nums[l];
                // maxsum = max(maxsum,sum);
                l++;
            }
            r++;
        }
        
        return maxsum;
    }
};

三、双序列问题

1. 编辑距离--很重要的母题

迭代法：

定义：

和一般的子序列问题一样，我们对dp数组的定义为：

dp[i][j] 为以word1[i-1]和word2[j-1]结尾的两个字符串的编辑距离

为了方便初始化,后面会细说

转移方程：
这里的转移方程是最复杂的，我们要分别求解不同操作对dp[i][j]的影响。

注意：我们要从后往前操作，因为在前面插入会导致前面字符的索引更改！！！

比较word1[i]和word2[j]

下文依据：

d[i][j]进行一步操作后变为dp[k][m],就离最短编辑距离更近了，因此dp[i][j] = dp[k][m]+1

插入：

dp[i][j] = dp[i-1][j]+1//在word2将word1[i-1]插入在word2[j-1]后面

dp[i][j] = dp[i][j-1]+1//在word1将word2[j-1]插入在word1[i-1]后面

删除：

dp[i][j] = dp[i-1][j]+1//在word1将word1[i-1]删除，然后i前移

dp[i][j] = dp[i][j-1]+1//在word2将word2[j-1]删除，然后j前移

替换：

dp[i][j] = dp[i-1][j-1]+1//在word1或者word2进行替换,i,j同时前移

相等：

dp[i][j] = dp[i-1][j-1];

因此，转移方程为：

           if(s1[i-1] == s2[j-1])dp[i][j] = dp[i-1][j-1];
           else{
                dp[i][j] = min(
                        dp[i][j-1]+1,
                        dp[i-1][j]+1,
                        dp[i-1][j-1]+1
                );
           }

初始化：
我们要知道，什么时候能一眼看出答案——当其中一个字符串为空时，这里就涉及到dp数组的定义了，因为如果dp[i][j]为word1[i]和word2[j]结尾的子串的编辑距离，那么对于长度为0的字符串（空串）就无法定义，因此，我们设置dp[i][j] 为word1[i-1]和word2[j-1]结尾的子串的编辑距离

同时，注意dp 数组的每个维度比相应的字符串长度多一个单位，以便包含空字符串的情况。这就是为什么数组大小是 m+1 x n+1。因此初始化如下：

        vector<vector<int>> dp(m+1,vector<int>(n+1,0));
        // for(int i = 0;i < m;i++)
        //     dp[i][0] = i;
        // for(int j = 0;j < n;j++)
        //     dp[0][j] = j;
        for(int i = 0;i < m+1;i++)
            dp[i][0] = i;
        for(int j = 0;j < n+1;j++)
            dp[0][j] = j;

遍历顺序：

注意，这里我们虽然是从后往前处理，也就是说我们要先知道前面的才能处理后面的，因此遍历的时候需要从前往后遍历

另一方面可以这样思考：

如图

可以看出dp[i][j]是依赖左方，上方和左上方元素的，所以在dp矩阵中一定是从左到右从上到下去遍历。

将转移方程放入遍历中：

        for(int i = 1;i <=m ;i++)
            for(int j = 1; j <= n;j++) 
            {
                if(s1[i-1] == s2[j-1])dp[i][j] = dp[i-1][j-1];
                else{
                    dp[i][j] = min(
                        dp[i][j-1]+1,
                        dp[i-1][j]+1,
                        dp[i-1][j-1]+1
                    );
                }
            }

最后，添加特殊处理的部分，代码如下：

class Solution {
public:
    int min(int a, int b, int c) {
        return std::min(std::min(a, b), c);
    }
    int minDistance(string s1, string s2) {
        int m = s1.size(),n = s2.size();
        if(m==0)return n;
        if(n==0)return m;
        //int* dp = new int[m][n];二维数组不好使用new的方式进行实现

        //int[][] dp = new int[m + 1][n + 1];这样是对的
        vector<vector<int>> dp(m+1,vector<int>(n+1,0));
        for(int i = 0;i < m;i++)
            dp[i][0] = i;
        for(int j = 0;j < n;j++)
            dp[0][j] = j;
        for(int i = 1;i <=m ;i++)
            for(int j = 1; j <= n;j++) 
            {
                if(s1[i-1] == s2[j-1])dp[i][j] = dp[i-1][j-1];
                else{
                    dp[i][j] = min(
                        dp[i][j-1]+1,
                        dp[i-1][j]+1,
                        dp[i-1][j-1]+1
                    );
                }
            }
        return dp[m][n];
    }

};

递归法：

先明确递归的思路:
我们如何从迭代转换到递归

首先,状态转移,初始化和dp的定义是不变的,那么我们首先思考如何将dp[i][j]中的i,j体现在dp递归函数中,显而易见,答案是,传入两个参数,i,j;

    int dp(string s1,int i,string s2, int j)

接着是初始化，这里本来可以设置 dp[i][j] 为以word1[i]和word2[j]结尾的两个字符串的编辑距离，但为了和迭代法统一，就延续上述设置

        if(i==0)return j;
        if(j==0)return i;

转移方程，与迭代法十分类似：

        if(s1[i-1] == s2[j-1])return dp(s1,i-1,s2,j-1);
        else return min(
            dp(s1,i-1,s2,j)+1,
            dp(s1,i,s2,j-1)+1,
            dp(s1,i-1,s2,j-1)+1
        );

注意，递归法有遍历顺序，但是是自动执行的，递归中会自动执行，所以迭代法中的for循环部分可以省去：
完整代码如下：

class Solution {
public:

    int minDistance(string s1, string s2) {
        int m = s1.length(), n = s2.length();
        return dp(s1, m, s2, n);
    }

    int dp(string s1,int i,string s2, int j){
        if(i==0)return j;
        if(j==0)return i;
        if(s1[i-1] == s2[j-1])return dp(s1,i-1,s2,j-1);
        else return min(
            dp(s1,i-1,s2,j)+1,
            dp(s1,i,s2,j-1)+1,
            dp(s1,i-1,s2,j-1)+1
        );
    }

    int min(int a, int b, int c) {
        return std::min(std::min(a, b), c);
    }
};

递归去重：

备忘录：

我们增加一个备忘录，将结果保存到备忘录的对应位置

memo = vector<vector<int>>(m+1, vector<int>(n+1, -1));

检测这个位置是否已经有值，有的话就不用再算了

        // 查备忘录，避免重叠子问题
        if (memo[i][j] != -1) {
            return memo[i][j];
        }
        // 状态转移，结果存入备忘录
        if (s1[i-1] == s2[j-1]) {
            memo[i][j] = dp(s1, i - 1, s2, j - 1);
        } else {
            memo[i][j] = min(
                dp(s1, i, s2, j - 1) + 1,
                dp(s1, i - 1, s2, j) + 1,
                dp(s1, i - 1, s2, j - 1) + 1
            );
        }
        return memo[i][j];

可能会疑惑，为什么能保证出现过一次的memo[i][j]就一定是最优解，后面不会更新比这个值更好的解吗？

我们可以看到，每次求解dp[i][j],都是使用三种状态，那么第二次对dp[i][j]进行处理的话，也会进行同样的处理，结果是没变的

因此，完整代码如下：

class Solution {
public:
    vector<vector<int>> memo;
    int minDistance(string s1, string s2) {
        int m = s1.length(), n = s2.length();
        memo = vector<vector<int>>(m+1,vector<int>(n+1,-1));
        return dp(s1, m, s2, n);
    }


    int dp(string s1,int i,string s2, int j){
        if(i==0)return j;
        if(j==0)return i;
        if(memo[i][j] != -1) return memo[i][j];
        if(s1[i-1] == s2[j-1])memo[i][j] =  dp(s1,i-1,s2,j-1);
        else memo[i][j] = min(
            dp(s1,i-1,s2,j)+1,
            dp(s1,i,s2,j-1)+1,
            dp(s1,i-1,s2,j-1)+1
        );

        return memo[i][j];
    }

    int min(int a, int b, int c) {
        return std::min(std::min(a, b), c);
    }
};

迭代法：

递归+备忘录：

可以看出，迭代法递归法复杂度相同时，由于递归不断调用函数产生资源消耗，其运行效率远不如迭代法

2. 最长重复子数组

dp数组（dp table）以及下标的含义

dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。（特别注意： “以下标i - 1为结尾的A” 标明一定是以A[i-1]为结尾的字符串）

(此处定义同编辑距离,为了初始化方便)

转移方程:

做过编辑距离后发现,此题比较简单,因为我们dp[i][j]必须包含nums1[i-1]和nums2[j-1],所以只需要比较nums1[i-1]和nums[j-1]即可,当他们不等时,dp[i][j]=0

因此,转移方程如下:

                if(nums1[i-1] == nums2[j-1]){
                    dp[i][j] = dp[i-1][j-1] + 1;
                    res = max(res,dp[i][j]);
                }

dp数组初始化

DP数组如下,我们发现我们需要对第一排和第一列进行初始化,才能顺利推导到后面的值

根据dp数组的意义,我们将其初始化为0即可

同时,由于某些dp值,我们会赋值为0,所以我们直接将所以初值都设置为0,当遇到应该为0的dp值,我们不更新即可,代码如下:

        vector<vector<int>> dp(nums1.size()+1,vector<int>(nums2.size()+1,0));

遍历顺序:
外层for循环遍历A，内层for循环遍历B。

外层for循环遍历B，内层for循环遍历A。都行

完整代码如下:

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>> dp(nums1.size()+1,vector<int>(nums2.size()+1,0));
        int res = 0;
        for(int i = 1;i <= nums1.size();i++)//边界问题
            for(int j = 1;j <= nums2.size();j++){
                if(nums1[i-1] == nums2[j-1]){
                    dp[i][j] = dp[i-1][j-1] + 1;
                    res = max(res,dp[i][j]);
                }
            }
        return res;
    }
};

3. 最长重复子序列

本题和最长重复子数组区别在于这里不要求是连续的了,所以dp数组的定义不用必须以nums[i]结尾了

确定dp数组（dp table）以及下标的含义:

dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]

转移方程 :

主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同

如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;

如果text1[i - 1] 与 text2[j - 1]不相同，虽然不能直接递增一位,但是两边字符串都增加了一位,这带来了新的可能性,我们不能从 text1[0,i - 2] 与 text2[0,j - 2]得到结果,,那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。

其实也就相当于,如果我们不能从dp[i-][j-1]推出dp[i][j],那就从dp[i-1][j]和dp[j-1][i]中想办法,因为dp[i-1][j]和dp[j-1][i]时对称的,我们就选择其中的更大值,如下图:

代码如下:

                if(text1[i-1] == text2[j-1]){
                    dp[i][j] = max(dp[i][j],dp[i-1][j-1]+1);
                }
                else{
                    dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
                }

初始化:
同样需要第一排和第一列的初值,且初始化都为0

确定遍历顺序:
从前向后，从上到下,进行两层循环

完整代码:

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        if(text1.size() == 0 || text2.size() ==0)return 0;
        vector<vector<int>> dp(text1.size()+1,vector<int>(text2.size()+1,0));
    
        for(int i=1;i<=text1.size();i++)
            for(int j =1;j<=text2.size();j++){
                if(text1[i-1] == text2[j-1]){
                    dp[i][j] = max(dp[i][j],dp[i-1][j-1]+1);
                }
                else{
                    dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
                }
            }
        return dp[text1.size()][text2.size()];     
    }

};

这样的dp定义方式有一个优势,结果不用遍历dp数组

4. 不相交的线

本题就是寻找最长的公共子序列

代码如下:

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>> dp(nums1.size()+1,vector<int>(nums2.size()+1,0));
        for(int i = 1;i <= nums1.size();i++)
            for(int j = 1 ;j <= nums2.size();j++){
                if(nums1[i-1] == nums2[j-1]){
                    dp[i][j] = max(dp[i-1][j-1]+1,dp[i][j]);
                }else{
                    dp[i][j] = max(dp[i][j-1],dp[i-1][j]);
                }
            }
        return dp[nums1.size()][nums2.size()];
    }
};

5. 判断子序列

此题和其他题的区别在于,返回值位bool,因此会很容易将dp数组的值定义为bool型,但这样初始化很复杂,时间复杂度有点高,初始化如下:

class Solution {
public:
    bool isSubsequence(string s, string t) {
        int n = s.size(),m = t.size();
        vector<vector<bool>> dp(n+1,vector<bool>(m+1));
        for(int i = 0;i <= n;i++){
            dp[i][0] = false;
        }
        for(int j = 0;j <= m;j++){
            dp[0][j] = true;
        }
        for(int i = 1;i <= n;i++){
            for(int j = 1;j <= m;j++){
                if(s[i-1] == t[j-1])
                    dp[i][j] = dp[i-1][j-1];
                else{
                    dp[i][j] = dp[i][j-1];
                }
            }
        }
        return dp[n][m];
    }
};

因此我们选择dp[i][j]的含义为,有多少个匹配的字符,当匹配字符==s.size()时,就是true

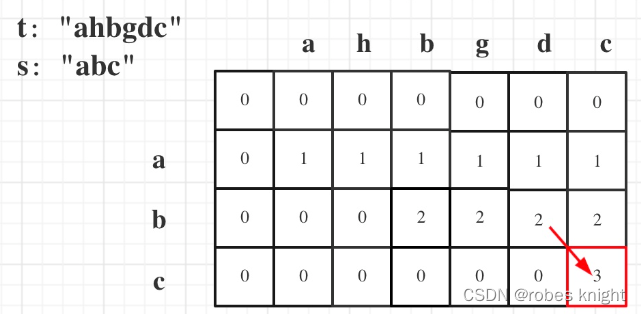
完整代码如下:

class Solution {
public:
    bool isSubsequence(string s, string t) {
        int n = s.size(),m = t.size();
        vector<vector<int>> dp(n+1,vector<int>(m+1,0));
        for(int i = 1;i <= n;i++){
            for(int j = 1;j <= m;j++){
                if(s[i-1] == t[j-1])
                    dp[i][j] = dp[i-1][j-1]+1;
                else{
                    dp[i][j] = dp[i][j-1];
                }
            }
        }
        return dp[n][m] == s.size() ? true : false;
    }
};

6. 不同的子序列-双序列中只改变单序列的典例

(1)dp定义:
dp[i][j]：[0,i-1]的s子序列中出现[0,j-1]的t的个数为dp[i][j]。(区间)

(2)转移方程:
此题与其他题不一样,因为是求有多少种删除方法,所以dp数组的更新不能是简单的+1

这里是求总的方法数,那当 s[i-1]==t[j-1]时:

我们不能只考虑将 s[i-1] 和 t[j-1] 同时留下,也即是dp[i][j] =dp[i-1][j-1] (最后一位相互抵消了)

还要考虑,如果前面也有一位 s[k] == s[i-1] (且相对位置满足t的要求),那么我们可以同时留下 s[k] 和 t[j-1] ,将 s[i-1] 删掉,因此dp[i][j] = dp[i-1][j](如果前面不存在s[k],那么此处为0,结果不变)

因为这两种情况时分开讨论的,不相交,因此当s[i-1]==t[j-1]时:

dp[i][j] = dp[i-1][j-1] + dp[i-1][j];

而当s[i-1]!=t[j-1]时:

我们考虑将s[i-1]删除,因为不相等用不到

但是不能删除t[j-1],因为我们在求d[i][j],j对应的就是t[0,j-1],要是将t[j-1]去除,那就不能称为dp[i][j]了(

因为t是子串不能更改),所以不存在dp[i][j-1]和dp[i-1][j-1]两种情况

因此转移方程如下:

                if(s[i-1] == t[j-1])
                    dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
                else{
                    dp[i][j] = dp[i-1][j];
                }

(3)初始化:

以样例为参考:

代码如下:

        vector<vector<unsigned long long>> dp(n+1,vector<unsigned long long>(m+1,0));
        for(int i = 0;i <= n;i++)
            dp[i][0] = 1;

(4)遍历顺序

两层for循环即可

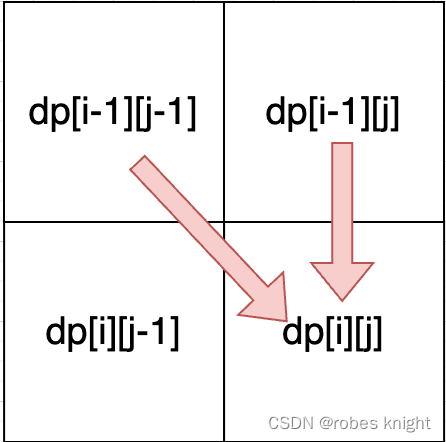
完整代码如下:

class Solution {
public:
    int numDistinct(string s, string t) {
        int n = s.size(),m = t.size();
        vector<vector<unsigned long long>> dp(n+1,vector<unsigned long long>(m+1,0));
        for(int i = 0;i <= n;i++)
            dp[i][0] = 1;
        for(int i = 1;i <= n;i++)
            for(int j = 1;j <= m;j++){
                if(s[i-1] == t[j-1])
                    dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
                else{
                    dp[i][j] = dp[i-1][j];
                }
                // dp[i][j] = dp[i][j] % (1000000007);
            }
        return dp[n][m];
    }
};

7. 两个字符串的删除操作

编辑距离的简化版

(1) dp定义:
不要连续就,定义dp[i][j]表示word1[0,i-1],word2[0,j-1]的最小步数

(2)转移方程

和编辑距离类似

word1[i-1] == word2[j-1]时,不删除,dp[i][j] = dp[i-1][j-1];

word1[i-1] != word2[j-1]时,在三种删除中选择最小的

                if(word1[i-1] == word2[j-1])
                    dp[i][j] = dp[i-1][j-1];
                else{
                    dp[i][j] = min(
                        dp[i-1][j-1]+2,
                        dp[i-1][j]+1,
                        dp[i][j-1]+1
                    );

(3)初始化

根据样例进行如下初始化:

代码:

        vector<vector<int>> dp(n+1,vector<int>(m+1));
        
        for(int i = 0;i <= n;i++)dp[i][0] = i;
        for(int i = 0;i <= m;i++)dp[0][i] = i;

(4)遍历顺序

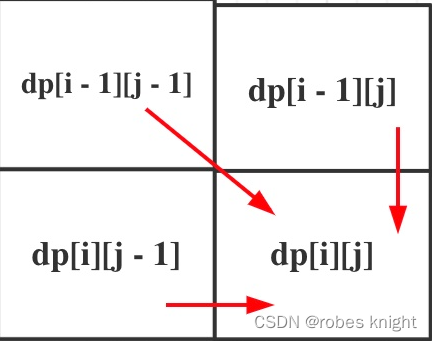
完整代码:

class Solution {
public:
    int min(int a,int b,int c){
        return std::min(std::min(a,b),c);
    }

    int minDistance(string word1, string word2){
        int n = word1.size(),m = word2.size();
        vector<vector<int>> dp(n+1,vector<int>(m+1));
        
        for(int i = 0;i <= n;i++)dp[i][0] = i;
        for(int i = 0;i <= m;i++)dp[0][i] = i;

        for(int i = 1;i <= n;i++)
            for(int j = 1 ;j <= m; j++){
                if(word1[i-1] == word2[j-1])
                    dp[i][j] = dp[i-1][j-1];
                else{
                    dp[i][j] = min(
                        dp[i-1][j-1]+2,
                        dp[i-1][j]+1,
                        dp[i][j-1]+1
                    );
                }
            }
        return dp[n][m];
    }
};

8. 两个字符串的最小ascii删除和

和上一题及其类似,只是初始化和更新转移方程的形式有点区别,不多赘述

代码如下:

class Solution {
public:

    int min(int a,int b,int c){
        return std::min(std::min(a,b),c);
    }

    int minimumDeleteSum(string s1, string s2){
        int n = s1.size(),m = s2.size();
        vector<vector<int>> dp(n+1,vector<int>(m+1));
        
        for(int i = 0;i <= n;i++)
            for(int j = 0;j < i;j++)
                dp[i][0] += int(s1[j]);
        for(int i = 0;i <= m;i++)
            for(int j = 0;j < i;j++)
                dp[0][i] += int(s2[j]);

        for(int i = 1;i <= n; i++)
            for(int j = 1 ;j <= m; j++){
                if(s1[i-1] == s2[j-1])
                    dp[i][j] = dp[i-1][j-1];
                else{
                    dp[i][j] = min(
                        dp[i-1][j-1]+int(s1[i-1])+int(s2[j-1]),
                        dp[i-1][j]+int(s1[i-1]),
                        dp[i][j-1]+int(s2[j-1])
                    );
                }
            }
        return dp[n][m];
    }
};

四、回文子串和子序列

(1)回文子串要求连续,可以用双指针进行解答;

(2)但是回文子序列不连续,双指针失效,可以复制一份然后,将其倒转,使用双序列的方法进行解答.

1. 回文子串

使用双指针解法,相比dp解法时间复杂度更低

代码如下,细节参考数组一章,双指针部分:

class Solution {
public:
    int jud(string s,int l,int r){
        int count = 0;
        while(l >=0 && r <s.size()&&s[l]==s[r]){
            l--;
            r++;
            count++;
        }
        return count;
    }
    int countSubstrings(string s){
        int count = 0;
        for(int i = 0;i < s.size();i++){
            count += jud(s,i,i);
            count += jud(s,i,i+1);
        }
        return count;
    }
};

2. 最大回文子序列

将s复制一份再倒转,然后对两个序列求最大公共子序列,代码如下:

//复制一份,倒转,求最大公共子序列
class Solution {
public:
    int longestPalindromeSubseq(string s) {
        string t = s;
        reverse(s.begin(),s.end());
        int n = s.size();
        vector<vector<int>> dp(n+1,vector<int>(n+1,0));
        for(int i = 1;i <= n;i++)
            for(int j = 1;j <= n;j++){
                if(s[i-1]==t[j-1])dp[i][j] = dp[i-1][j-1] + 1;
                else{
                    dp[i][j] = max(max(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1]);
                }
            }
        return dp[n][n];
    }
};