决策树

1 决策树

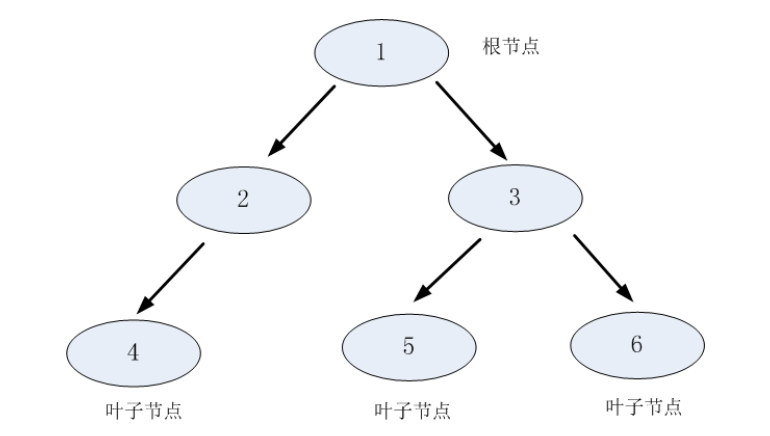
分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点（node）和有向边（directed edge）组成。结点有两种类型：内结点（internal node）和叶子结点（leaf node）。内部结点表示一个特征或属性，叶结点表示一个类。

用决策树分类，从根结点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到其子结点；这时，每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配，直至达到叶结点。最后将实例分到叶结点的类中。

决策树的构建是数据逐步分裂的过程，构建的步骤如下:

1. 将所有的数据看成是一个节点，进入步骤2；
2. 从所有的数据特征中挑选一个数据特征对节点进行分割，进入步骤3；
3. 生成若干子节点，对每一个子节点进行判断，如果满足停止分裂的条件，进入步骤4；否则，进入步骤2；
4. 设置该节点是子节点，其输出的结果为该节点数量占比最大的类别。

通过以上步骤，我们可以看出需要解决的两个问题：如何选择分裂的特征；停止分裂的条件是什么。

2 信息论基本概念

• 熵
  在信息论与概率统计中，熵（entropy）是表示随机变量不确定性的度量。设$X$是一个取有限个值的离散随机变量，其概率分布为$P\left(X=x_i\right)=p_i$，则随机变量X的熵定义为：$$H(X)=-\sum _{i=1}^n{p}_i\log p_i$$
• 条件熵
  条件熵$H(Y|X)$表示在已知随机变量X的条件下随机变量Y的不确定性。随机变量X给定的条件下随机变量Y的条件熵（conditional entropy）$H(Y|X)$，定义为X给定条件下Y的条件概率分布的熵对X的数学期望：$$H(Y|X)=\sum _{i=1}^{n}P\left(X=x_i\right)H(Y|X=x_i)$$
• 信息增益
  特征A对训练数据集D的信息增益$g(D,A)$，定义为集合D的经验熵$H(D)$与特征A给定条件下D的条件熵$H(D|A)$之差$$g(D,A)=H(D)-H(D|A)$$
• 信息增益比
  特征A对训练数据集D的信息增益比$g_R(D,A)$定义为其信息增益$g$