1. comsol 中的弱形式问题——一维稳态导热

最新推荐文章于 2024-06-09 15:24:27 发布

今日，真我，精彩

最新推荐文章于 2024-06-09 15:24:27 发布

阅读量1.8k

点赞数 2

分类专栏： COMSOL 文章标签：算法

本文链接：https://blog.csdn.net/reactortiger/article/details/130121448

版权

COMSOL 专栏收录该内容

1 篇文章 0 订阅

订阅专栏

弱形式推导的一般方法

写出问题的偏微分方程
乘以试函数并对方程进行积分
采用分部积分进行微分降级得到方程的弱形式

一维稳态导热微分方程的弱形式

1.问题描述

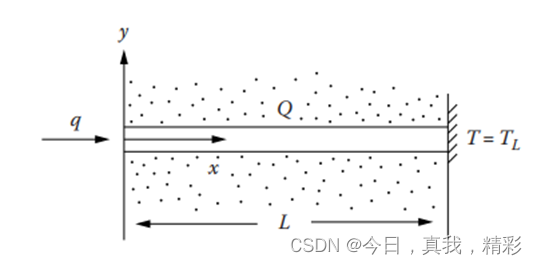
如图所示，一根长度为 L=1m的金属棒，左端有恒定热量 q =10W/m2流入，右端保持恒定温度 TL=300K, 有电流流过金属，恒定产热量为 Q=20W/m3，热导率 k=2W/(m.K)为常数，求金属棒上的温度分布。

2. 微分方程

傅里叶定律，也称热传导定律，描述热传导过程。其微分形式如下：

q=-k▽T

其中，q为局部热流密度，W/m2; k为材料热导率，W/(m.K)

一维情况下为：

$\mathrm{q=-k}\frac{dT}{dx}$

将问题描述转化为数学语言，因存在内部热源 Q(W m^-3)，故控制方程为：

$\nabla \cdot \left( -k\nabla T \right) =Q$

一维形式为：

$-k\frac{dT^2}{d^2x}=Q,\ 0<x<L$

边界条件为：

$\left\{ \begin{array}{l} -k\frac{dT}{dx}=q,\ x=0\\ T=T_L,\ \ \ \ \ x=L\\ \end{array} \right.$

3.方程求解

$T\left( x \right) =T_L+\frac{q}{k}\left( L-x \right) +\frac{Q}{2k}\left( L^2-x^2 \right)$

4. 方程的弱形式

4.1乘上试函数并积分(test function)

等式两边同时乘上试函数Φi ( x )，再进行一次积分，则：

$\int_0^L{\phi _i\left( x \right)}\left( -k\frac{dT^2}{d^2x}-Q \right) dx=0$

4.2 分部积分降低微分阶数

上述方程可变形为：

$\int_0^L{\phi _i\left( x \right)}\left( -k\frac{dT^2}{d^2x} \right) dx-\int_0^L{\phi _i\left( x \right)}Qdx=0$

利用分步积分法消去二阶导项：补充：∫ u d v = u v − ∫ v d u，那么上式变成

$\int_0^L{}k\frac{dT}{dx}\frac{d\phi _i}{dx}dx-\phi _i\left( x \right) .k\frac{dT}{dx}\left| \begin{array}{c} L\\ 0\\ \end{array} \right. -\int_0^L{\phi _i\left( x \right)}Qdx=0$

此即为弱形式表达式。可见在进行一次积分之后，消除了二阶项，但同时放宽了解要求，因此称之为weak form

5.在comsol中的表现形式

5.1 comsol 弱表达式方程

在comsol中弱形式方程的形式如下：

对比上式，积分方程中可以表达为

$0=\int_{0}^{L}\left(-k\frac{d\phi_i}{dx}\frac{dT}{dx}+\phi_i(x)Q\right)dx-\phi_i\left(x\right).(-k\frac{dT}{dx}\left|{L\atop0}\right.)$

故方程在comsol中的弱表达式即为右边的积分项：

-k*test(Tx)*Tx+Q*test(T)

其中，test(Tx)为试函数的导数，test(T)为试函数；Tx为温度的导数

5.2 边界条件

该问题中有两个边界条件，边界方程如下

${-\phi}_i\left(x\right).\left(-k\frac{dT}{dx}\left|{L\atop0}\right.\right)={-q}_L.\phi_i\left(L\right)+q_0.\phi_i\left(0\right)$

（1）在x=0处指定了热通量q，其方向向右为+，故在comsol中添加弱贡献项如下：

q*test(T)

（2）在x=L处指定了温度TL,所以在comsol中添加弱贡献项如下：

-u*test(T)-test(u)*(T-TL)

其中u为辅助因变量，以保证采用通量的形式使得L处的温度为TL。

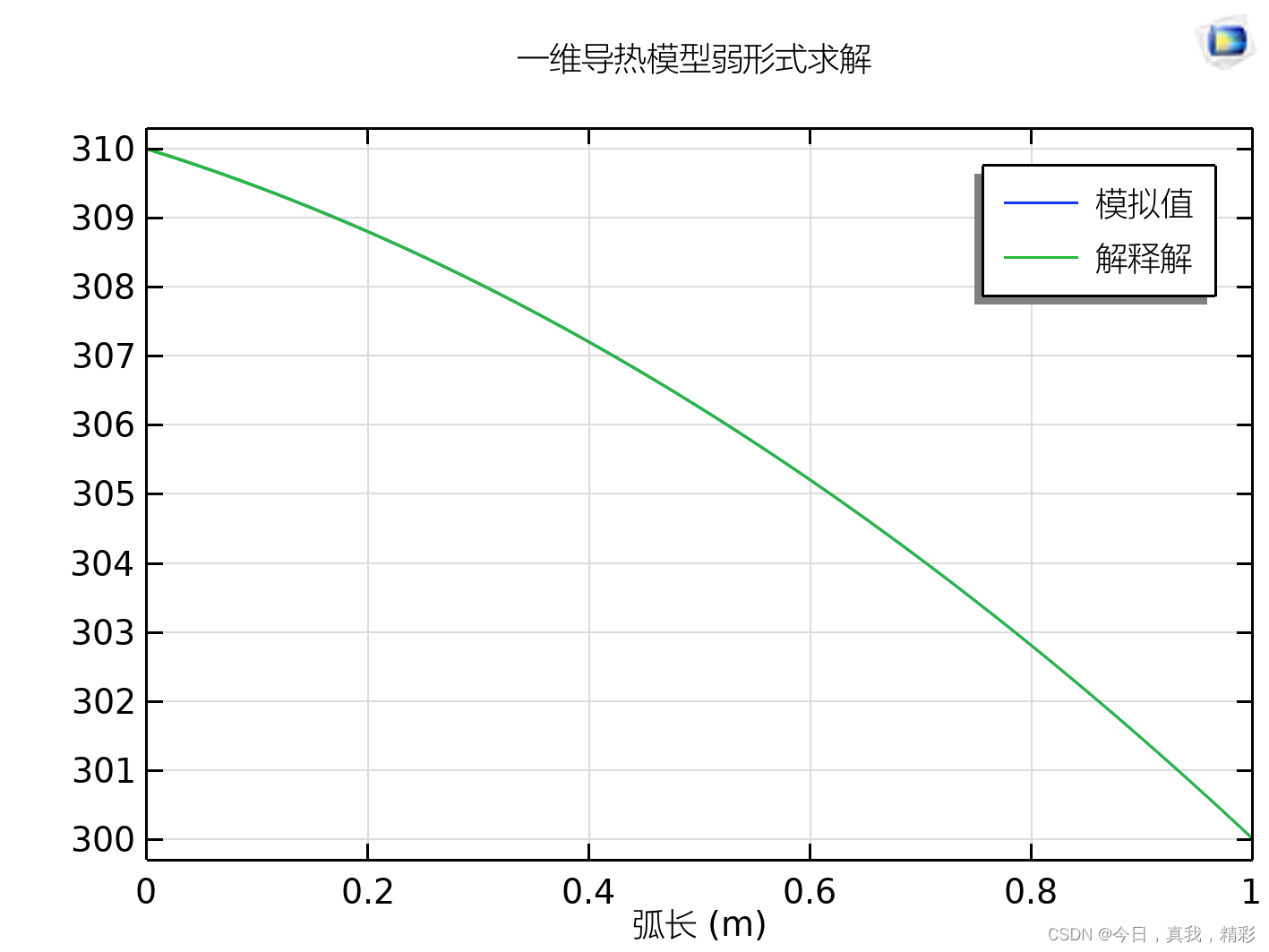
求解的结果如图

今日，真我，精彩

关注

2
点赞
踩
7

收藏

觉得还不错? 一键收藏
1
评论
1. comsol 中的弱形式问题——一维稳态导热

comsol弱形式的求解
复制链接

扫一扫

专栏目录

1. comsol 中的弱形式问题——一维稳态导热

“相关推荐”对你有帮助么？