dp——动态规划练习2（二叉搜索树的构建+一些小例子和之前的优化）

二叉搜索树

定义

二叉搜索树，就是二叉查找树、二叉排序树，说白了就是一个思想：
用一棵树存储一些元素值，其中我们保证左子树结点均小于根节点，右子树结点均大于根节点。
直接从之前的博客中嫖了一张图：

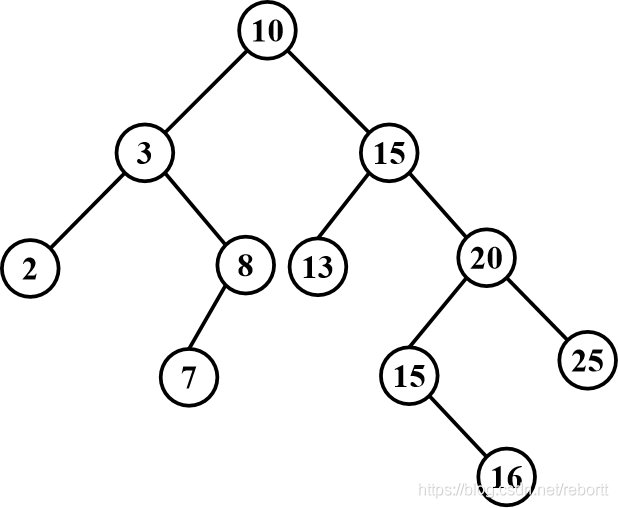
这颗树有很多很好的性质：

• 首先中序遍历的结果是从小到大递增的，可以用于排序
• 在查找的过程中，我们只需要从根节点出发，和跟结点对比即可，如果树的构建比较好，那么我们就可以保证O(logn)的查找效率
• 这棵树还有一种形式，将每一个单分支结点和叶子节点都补上结点，构成一种新的树。
  
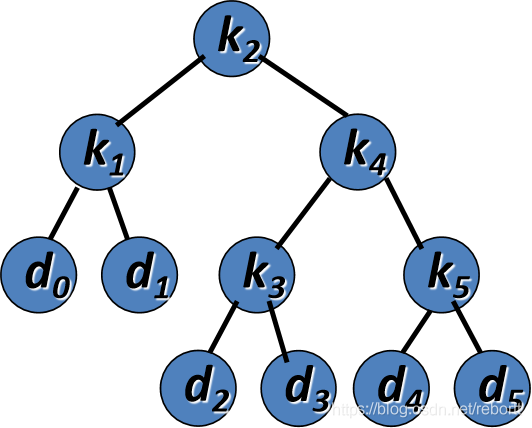
  我们可以看出，新补充的结点都是叶子节点，他们不属于某一个特定的数值，而是一个范围，查找失败的范围。

如何构建最优二叉搜索树

所以接下来我们的任务就是按照搜索的特点构建一个最优的二叉搜索树。
这个搜索的特点可能让人有点懵，其实和哈夫曼树差不多，这里的搜索是有一个概率的，不论是搜索成功还是失败（到达叶子节点）。

输入

• 大小为n的数组(1-n)，存储的是每一个非叶子结点的数值信息；
• 大小为n的数组(1-n)，存储非叶子结点的查找概率p
• 大小为n+1的数组(0-n)，存储叶子结点的查找概率q

输出
查找代价最低的二叉搜索树

代价？
这里我们要知道，每一次搜索的时候都需要和根节点比较，每一次比较都有一个代价。
如果将一个查找率很高的结点放在下面，那么代价就会很大。

叶子结点是非叶子节点+1，因为每一个非叶子节点都有两个孩子节点，这个就不需要我再证明了吧。

分析一下，子问题就不用说了，我们都是树结构了，子问题也是重叠的。
然后证明最优子结构，这个……就自己脑补一下，如果有一个子问题不是最优的，那整体也不可能是最优的。

实现

我们先放一下存储结构，因为不太好想。
先给出几个定义吧，首先是E[i][j]，表示从第i个到第j个结点的最小二叉搜索树。

如果j = i-1，说明只有一个叶子节点 i-1
E[i][j] = q_i-1
如果j =>i，
E[i][j] = min{ E[i][r-1]+E[r+1][j]+p_r+a }，其中i <= r <= j

（j = i-1可能有一点费解，这是因为我们加入了叶子结点的原因，这是表示只有一个叶子节点）

如果是只有一个叶子节点，说白了就是查找失败，那么就只需要有叶子节点的代价即可；
但如果是多个结点（包括一个结点），我们需要将其拆分成两个树，从i到r-1和r+1到j，然后将r作为根节点，查找次数为1，代价为p_r，这也是前三项的由来。
这里我们有一个a，是因为我们将两棵树都增高了一层，所以我们需要加上多的这部分的代价，我们简写成a，可以看出a的代价就是两棵子树的所有结点对应的概率*1，再算上p_r，其实就是E[i][j] = E[i][r-1]+E[r+1][j]+Σi到j的所有节点的概率，我们将这个概率记为W[i][j]。

所以我们在计算E[i][j]不但需要两个子树的代价，还需要W[i][j]的代价。那么我们先来计算W[i][j]的代价。

W[i][i-1] = q_i-1，是因为只有一个叶子节点
W[i][j] = W[i][j-1]+p_j+q_j，即在原来的基础上加一个叶子节点再加一个j结点（两个非叶子结点之间一定是有一个叶子节点的，并且这个叶子节点的下标应该和后一个非叶子结点相同，因为叶子节点下标从0开始，非叶子节点从2开始）

其实写成这样，我们的存储格式也就很明显了，就是在一个二维方阵中，行数和列数都是元素个数加一，不过这个格式也有点绕。

行数准确来说是叶子节点的个数，因为需要存储W[i][i-1]这样的结点，所以列数要比元素个数多一个，更好行数和列数就相同了。我们用n=4来举例吧。

W10	W11	W12	W13	W14
	W21	W22	W23	W24
		W32	W33	W34
			W43	W44
				W54

我们填入的方式是这样的，首先将主对角线进行填充，按照定义对角线分别为q0-4，然后接下来还是按照对角线填充，按照我们的定义来就行了。

在得到了W矩阵之后，我们就可以开始进行E矩阵的计算了。
此时我们的定义是这样的：

E[i][i-1] = q_i-1
E[i][j] = min{ E[i][r-1]+E[r+1][j]+W[i][j] }，其中i<=r<=j

伪代码

伪代码是同时实现的W、E矩阵，
另外我们还是采用矩阵链乘法的对角线遍历方式来实现循环的，

Optimal-BST(p, q, n)
//初始化
For  i=1  To  n+1   Do
      E(i, i-1) = qi-1;
      W(i, i-1) = qi-1;
      
For  l=1  To  n   Do				//对角线为l
	For   i=1   To   n-l+1   Do		//对角线上元素的横坐标i
	    j=i+l-1;					//按照l和i计算纵坐标j
		E(i, j) = ∞;
        W(i, j)=W(i, j-1)+pj+qj;
        For  r=i  To  j   Do
        	temp=E(i, r-1)+E(r+1, j)+W(i, j);
            If	temp<E(i, j)
            	E(i, j)=t;  
            	//Root(i, j)=r;
Return  E and  Root   

其中的root矩阵是我们用来记录二叉搜索树的根节点位置的矩阵。
在调用的过程中我们还是采取递归的方式，首先调用函数，传递参数i = 1，j = n，在函数内部我们先查看j是否等于i，如果是则直接打印这个结点，否则在矩阵中查找root[i][j]的值，确定两个子树分别调用函数，最后记得补上叶子节点即可。

习题——堆石子

在一条直线上有 n 堆石子，每堆有一定的数量，每次可以将两堆相邻的石子合并，合并
后放在两堆的中间位置，合并的费用为两堆石子的总数。求把所有石子合并成一堆的最
小花费(定义 dp[i][j]为第 i 堆石子到第 j 堆合并的最小花费)。

这里我们只给出递推方程，只要有了方程，剩下的实现问题都不大。
首先，如果是只有一堆石子（dp[i][i]），不需要合并，代价为0
否则dp[i][j] = min{ dp[i][k] + dp[k+1][j] +Σm[i…j] }，即两个子问题的代价和，再加上涉及到的所有石子堆的代价和。

得到了方程，确定为二维的n阶方阵，先填入临界值然后按照定义即可。（和矩阵链乘法相似，在之前的博客中有涉及）

习题——LCS 的优化

滚动数组

LCS就是我们之前提到的最长公共子序列，我们之前还提到了有一个叫滚动数组的概念，是用来进行dp问题的优化的。那么我们就来看一下。
之前我们定义的矩阵大小是m行n列的，但是我们的C[i][j]只和左上角、左边和上面的元素有关，剩下的元素都不是直接作用的，那么我们是否可以在这上面动手脚？

首先，我们只创建一个两行n列的二维数组，先在第一行进行初始化，还有第一列。
然后我们就可以通过这些来进行第二行的创建了。
在两行都填满了之后，我们就不再需要第一行的内容了，那么我们就可以让数组滚动起来，用第一行接着存储第三行的内容。（这样会特别不好实现，所以还是将第二行向上移动一下比较舒服）

当然了，我们也可以只使用两列来实现。

其他的呢

首先，我们的矩阵链乘法和比较类似的堆式子问题，都是需要对角线填值（还有二叉搜索树），很明显需要的不只是几行或者几列，我们的零一背包问题则可以考虑。

所以，我们也算是得到了一个小结论，如果是需要多项对比来填值的（一般为对角线方式填值）不能使用滚动数组，但是如果是只需要几项比较（固定在上下行或者是左右列的那种），可以考虑一下。

B数组的问题

这里再说一下B的问题吧，其实也不是真的需要，在我们得到了C矩阵后，从最后按照B的定义来回溯，也能正确的找到最长公共子序列，而且时间复杂度为O(m+n)。
最快max{m,n}就能找到（尽量走对角线）
最慢也是m+n的代价（没有相同的，即没有走对角线的那种情况）

习题——找硬币问题

这个应该是在leecode上都有的。

题目描述：
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以
凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，
返回-1。（提示：你可以认为每种硬币的数量是无限的）。
示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
示例 2:
输入: coins = [2], amount = 3
输出: -1

这个题就是使用一个一维数组将每一个金额对应的最小硬币数目都存起来，
然后A[amount] = min{ A[amount-coins[i] ] +1 }，也就是先用一个硬币找零，看看剩下的金额中的最少需要几个。
比如找25元，我们可以先找1元，然后看看24应该怎么找钱，然后再试试先找5元，看看二十怎么办。

初始值就是刚好为硬币金额的为1，小于最小硬币金额的为0，然后从左到右一个个找过去就行了。

习题——01背包问题中背包的内容

我们在解决了01背包问题后，还没有好好看一下怎么进行回溯最优解，这次我们补上。
首先，我们不能为每一个矩阵的每一个点都构建一个数组来存储01串吧，明显不合适，
另外我们之前都是使用递归的方式，从最后到问题的最开始（初始值）找回去的，
所以我的想法还是要利用递归的方式，一步步回溯出整体来。

实际上我们的M[i][j]只有两种可能，要么内容和M[i+1][j]相同，要么是m[i+1][j-wi]+vi，
所以我们先采用一个额外的数组B，来进行存储（这样看起来比较显然，随后我们会去掉这个数组）我们这个值的由来，如果是(i+1,j)就记录j，否则记录j-wi的值，
这样在回溯的过程中，如果记录的值和当前相同，说明这个东西没有被放进去，我们就在下一行继续；否则就是放进去了，先打印这个东西，然后就需要从m[i+1][j-wi]位置处继续了。
当我们到达了最后一行，就直接通过该处的值是否为0判断有没有放回去即可。

//M为dp数组，B为刚才的记录矩阵，n为物品个数，ij为下标
zero_one_knapsack(M,B,n,i,j)	//初始调用为M、B、n、1、C
if(n == i)						//到达最后一行
	if(M[i][j])					//最后一个物品放进去了
		printf n
else
	if(M[i][j] == j)			//没放进去，直接调用函数
		zero_one_knapsack(M,B,i+1,j);
	else 						//放进去了，需要打印一下
		zero_one_knapsack(M,B,i+1,M[i][j]);
		printf i

当然了，我们在LCS中可以放弃B数组，在这里一样可以，不过这时需要我们自己去判断从哪里来的了。
如果是放不放是一样的，那么我们在打印过程中就无所谓了，找一种就行了。