GAME101-Lecture04学习_mpersp!ortho-CSDN博客

本文链接：https://blog.csdn.net/rempter/article/details/137980016

课程链接

【GAMES101-现代计算机图形学入门-闫令琪】 https://www.bilibili.com/video/BV1X7411F744/?p=4&share_source=copy_web&vd_source=8332072dc5586e92174abc96d6e4280f

二维旋转矩阵的补充

第一行的式子，是上节讲到的二维的旋转矩阵（二维的变换不用齐次坐标表示的话，基本就是这种2*2的矩阵表示）

第二行的式子，旋转-θ角。是将第一行的所有θ替换成-θ，然后化简得来的。

观察可以发现，旋转-θ的旋转矩阵，就是旋转θ的旋转矩阵的转置。
另外也可以，旋转-θ的旋转矩阵，也是旋转θ的旋转矩阵的逆。（第三行的式子。通过矩阵的定义，矩阵转成逆矩阵可知）
从而可以得到性质：在旋转里，旋转θ的旋转矩阵的转置等于旋转θ的旋转矩阵的逆（在数学上，一个矩阵的逆等于它的转置，这个矩阵就是正交矩阵）
如果想要让二维物体沿着相反的方向旋转相同的角度，那么写出一个正向旋转矩阵，然后转置即可。

三维变换的补充

通过升维来表示三维变换。

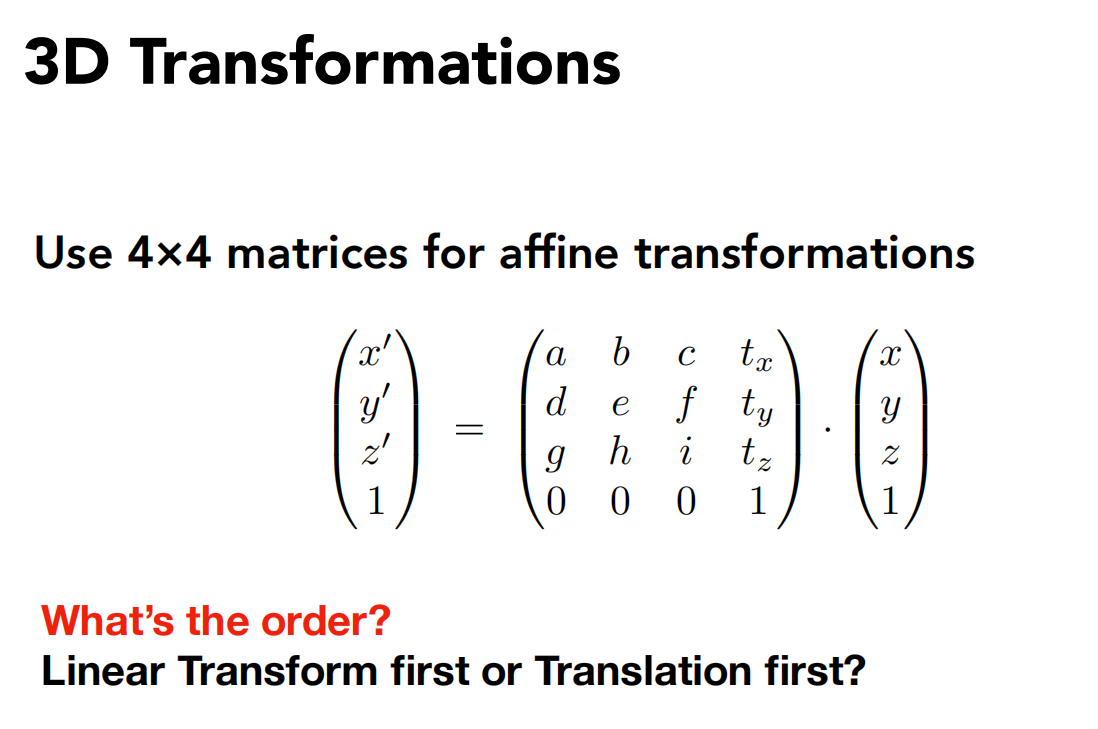
和二维的变换一样，三维的仿射变换也是线性变换再平移变换的。

缩放和平移（变换）

旋转（变换）

旋转变换矩阵

三维的旋转分为绕着x、y、z三个轴旋转的情况。

第一个式子中是绕着x轴旋转，可以发现：

x的值是不变的。因此在左上角3*3的线性变换矩阵中，其第一行和第一列都是100（图中蓝色框框）
y的值和z的值都是旋转的。因此左上角3*3的线性变换矩阵中，右下角的2*2的矩阵是变化的，这其实是因为y和z都旋转了相同角度。（图中红色框框）

第三个式子中是绕着z轴旋转，和绕着x轴旋转的情况分析方式一样。

第二个式子中是绕着y轴旋转，其式子就有些不同了。其旋转矩阵的值是其他的负值。

坐标系的建立是用向量叉乘的方式建立的。本门课用的是右手螺旋定则判断正负（方向）。
在确定x轴时可以用y叉乘z；z轴可以用x叉乘y。
而y轴，只能用z叉乘x，x叉乘z是负值，所以其旋转矩阵的值是其他的负值

欧拉角

从RX，Ry，Rz组成任意3D旋转?
所谓欧拉角
常用于飞行模拟器:滚转、俯仰、偏航

任意的一个旋转，都可以写成绕x、y、z旋转的组合。

三个轴旋转的旋转角，称为欧拉角。

罗德里格斯旋转公式

简单来说就是将任意的旋转写成一个旋转公式，该公式可以将旋转“分解”到三个轴上。

罗德里格斯公式提供了一个旋转矩阵，旋转矩阵定义了一个旋转轴n和旋转角度α。

这里旋转轴默认过原点，那么就是起点是原点，方向是n，旋转角度是α旋转。
如果要实现真正的绕任意轴旋转（即轴可以平移），那么就得平移这一条轴到能自转的情况（即让这个轴的起点与原点重合），先旋转（自传），转完再移回去。（所有的旋转都是自旋转，上节课提到的绕着某个点旋转也是得先平移让旋转点与原点重合，旋转完后再平移回去）
图中公式最后的大N，就要看这个公式的推导。闫老师把推导过程的pdf发了出来，配合这个视频（games101罗德里格斯旋转公式推导）大概是明白了怎么推到的。（但自己推那是真搞不定，只能说数学水平真的决定计算机的上限。。。）
推导过程中，有涉及到两个向量的叉乘。在进行两个向量的叉乘时，可以用矩阵的形式，因此才会出现最后面那个矩阵N。
（第二节的向量叉乘：）

在三维中的两个向量的叉乘方法，就是图中第一条式子。而叉乘也可以写成下方第二条式子的样子（矩阵的形式)。

四元数

四元数是为了给旋转做差值才引入的。

假设一个旋转矩阵是旋转15°，另一个是旋转25°。如果将两个矩阵加起来求平均，结果并不是20°。
这是因为旋转矩阵不适合做差值。

闫老师没有深入讲这个四元数，提了一嘴。后续自己会找些资料研究研究，毕竟unity里就有这个四元数。。

观测变换

变换其实是为了让三维的空间变成二维的图。

视图变换

引入

什么是视图转换
想想怎么拍一张照片 --一找个好地方，安排人(模式改造) --找一个好的“角度”来放相机(视图变换) --“茄子！”(投影变换)

模型视图投影变换，简称MVP变换。

视图变换矩阵

矩阵概念定义

怎么进行视图变换？
定义相机 --位置 --注视/凝视方向 --向上方向 (假设是 xx 观看)

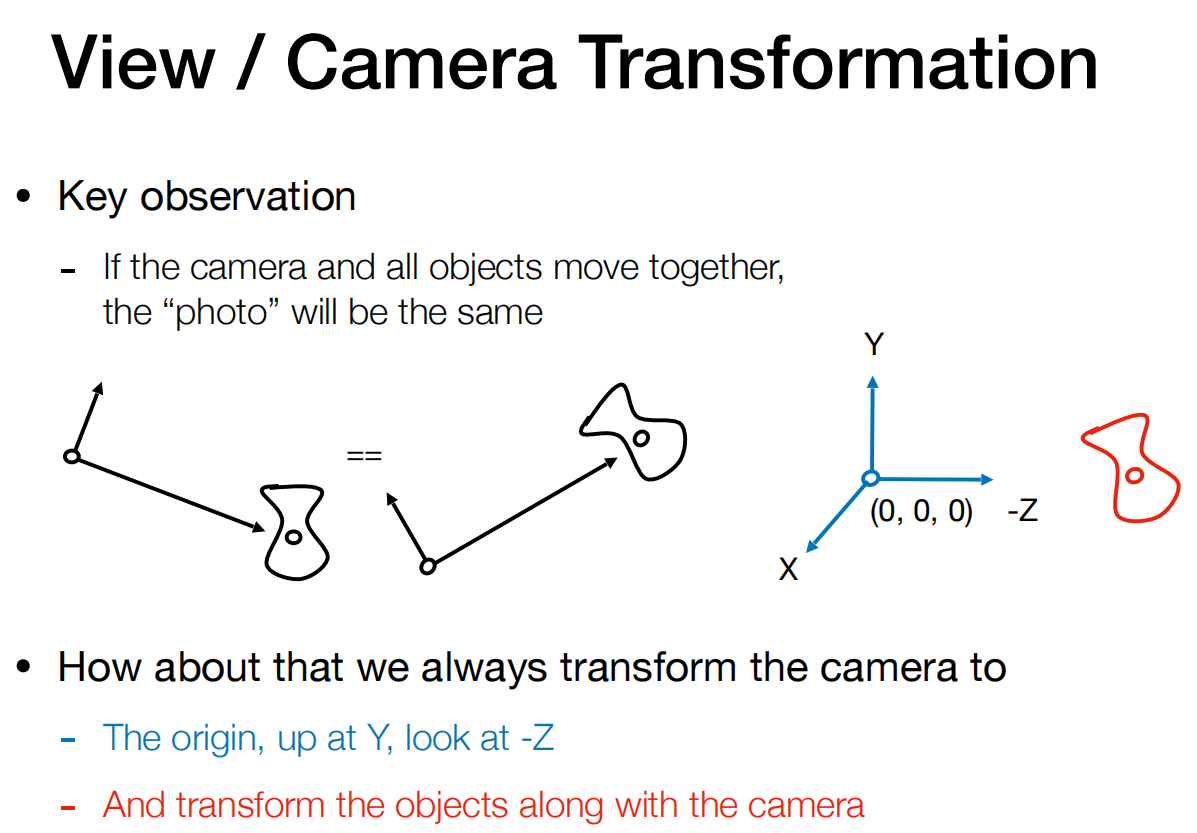
关键观察 --如果相机和所有对象一起移动，“照片”将是相同的
不如我们总是把摄像机转换成 --原点，在Y上，看-Z --与相机一起变换对象

用 Mview 变换相机 --它位于原点，在Y的上方，看-Z
M在数学中如何？ --将 e 平移到原点 --将g旋转到-Z --将t旋转到Y --旋转(g叉乘t 可以认为是图中绿色坐标轴) 至X --很难写!

矩阵推导

Mview如何计算？ -- Mview = Rview Tview
平移到原点（Tview就是平移矩阵）

这里是先平移（Tview平移矩阵）再线性变换（Rview旋转矩阵）。

对于Rview，我们需要将视图的坐标系转成标准的坐标系。即g旋转到-Z；t旋转到Y；(g叉乘t)旋转到X。这样运算不好算，所以反过来让标准坐标系转成转到视图的坐标系。图中最后一行，就是用种思想进行的公式推导：

Rview是视图的坐标系转成标准的坐标系的旋转矩阵。
Rview直接求不好求，我们反过来，先求Rview-1。（前面二维矩阵补充提到，“在旋转里，旋转θ的旋转矩阵的转置等于旋转θ的旋转矩阵的逆”。）
Rview-1的求法则是和前面求“旋转矩阵的ABCD”一样，用特殊值法。
Rview-1求出来，Rview-1 = Rview-T。
此时让Rview-T再转置回去就可以得到Rview。

投影变换

引入

投影

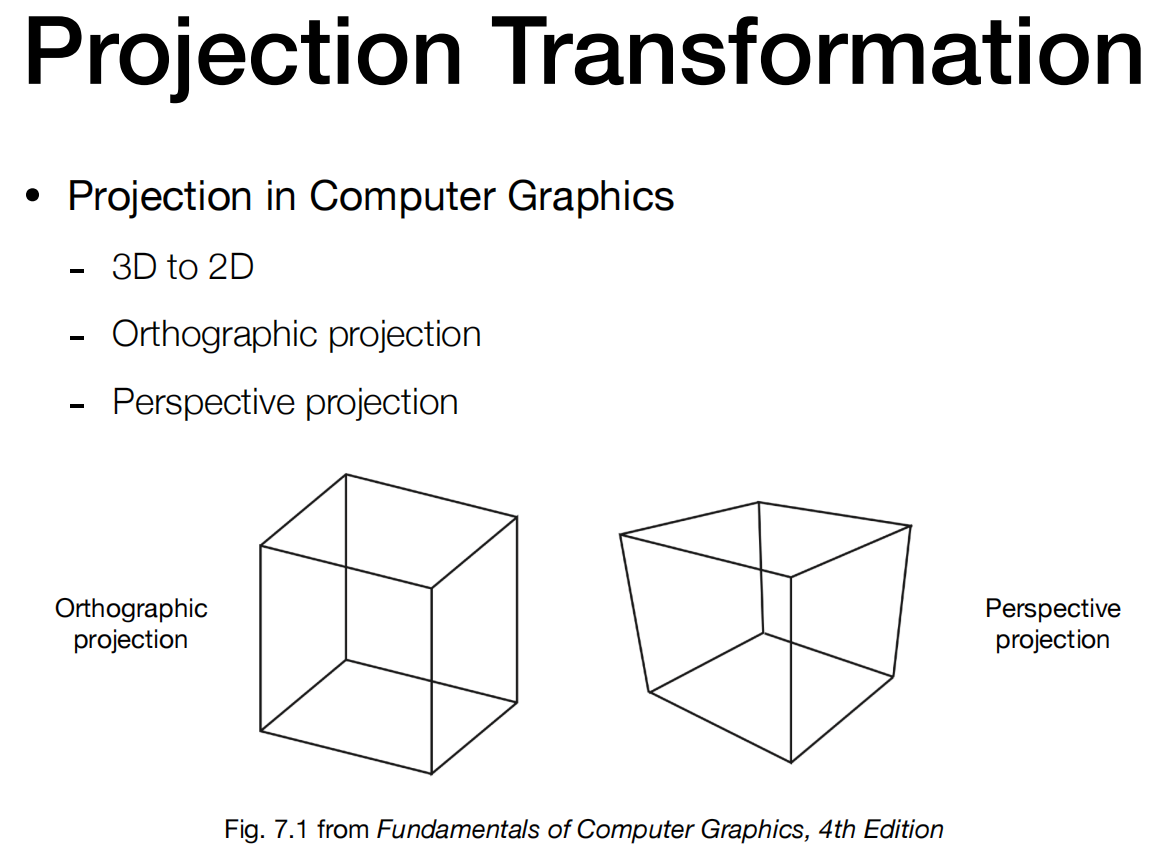
计算机图形学中的投影 --3D至2D --正交投影 --透视投影

上图的左下角是正交投影。正交投影并不会有近大远小的现象，透视会。

上图的右下角是透视投影。原本平行的两条边，在这种投影下，会有相交。这里更像是人眼睛的效果。

摄像机的成像方式

左侧透视投影，摄像机放在某一个位置上看作一个点。以摄像机点为起点，做射线形成空间的一个锥体（视锥体）。在椎体中，通过“最远”和“最近”的设定，将“最远”和“最近”的区域的东西全显示在进出的图片上。

正交投影

一个简单的方法来理解 --摄像头位于原点，看着-Z，向上看着Y(看起来很眼熟吗?) --删除Z坐标 --将生成的矩形平移并缩放至[-1,1]2

不管远处还是近处，全部放在一张图上。

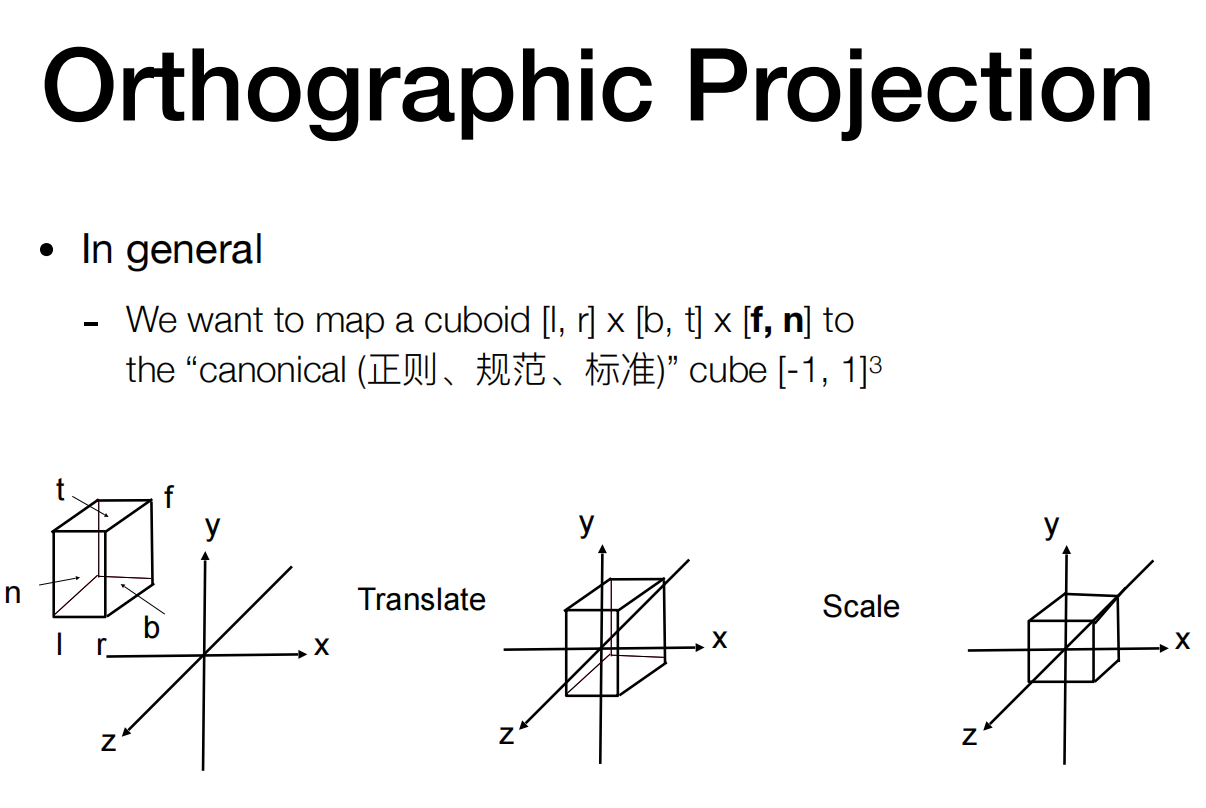
我们要把一个立方体[l,r] x [b,t] x [f,n]映射到“标准(正则、规范、标准)” 的立方体[-1,1]3上

空间中的任何一个立方体（最左侧的图），都可以通过平移、缩放等变换，变成一个标准的立方体（最右侧的图）。

x轴表示左右（立方体的[l,r]），y轴表示上下（立方体的[b,t]），而z轴是远近（立方体的[f,n]。注意离我们更远，z的值应该是更大的，f>=n。这就是一些API 比如OpenGL用左手系）

正交矩阵

先做平移，再做缩放。

透视投影

引入

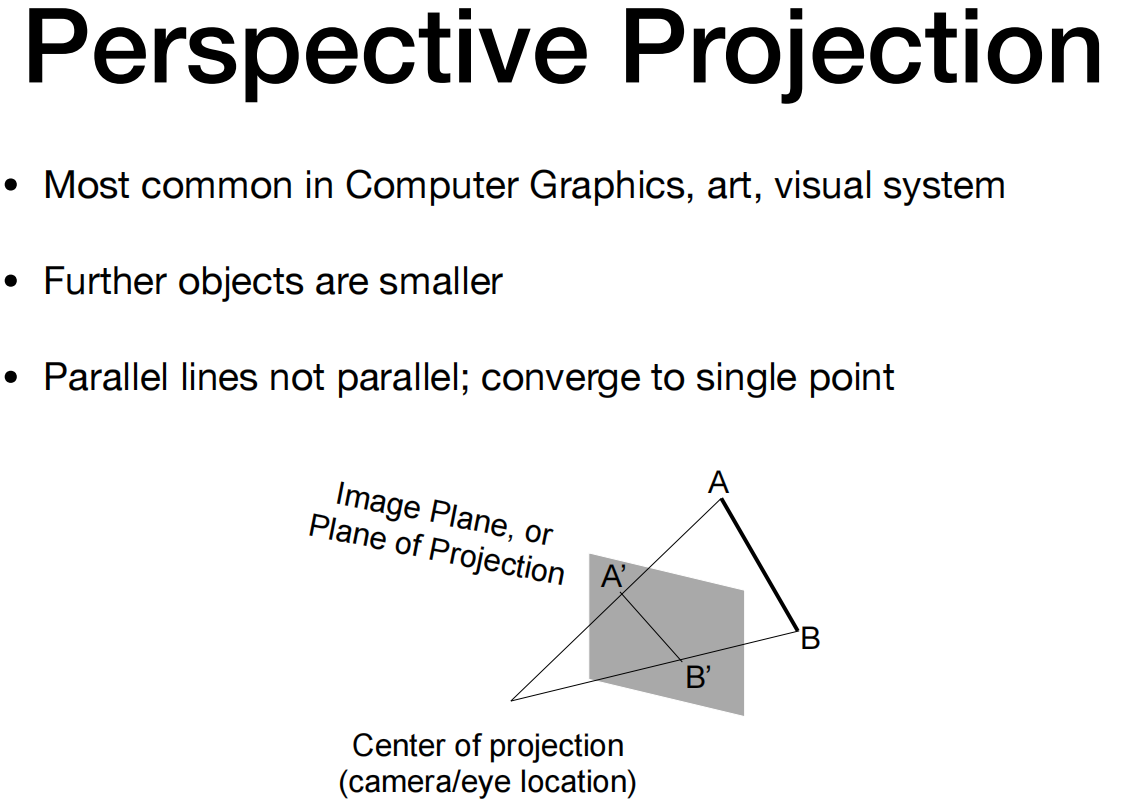
最常见于计算机图形学、美术、视觉系统
更远的物体更小
不平行的。平行线汇聚成一点。

齐次坐标中，(x,y,z,1)乘上任意不为0的数，在三维中的坐标都是不变的，都是(x,y,z)。

当(x,y,z,1)乘上z时，(xz,yz,z2)在三维中还是(x,y,z)。

“挤压”投影

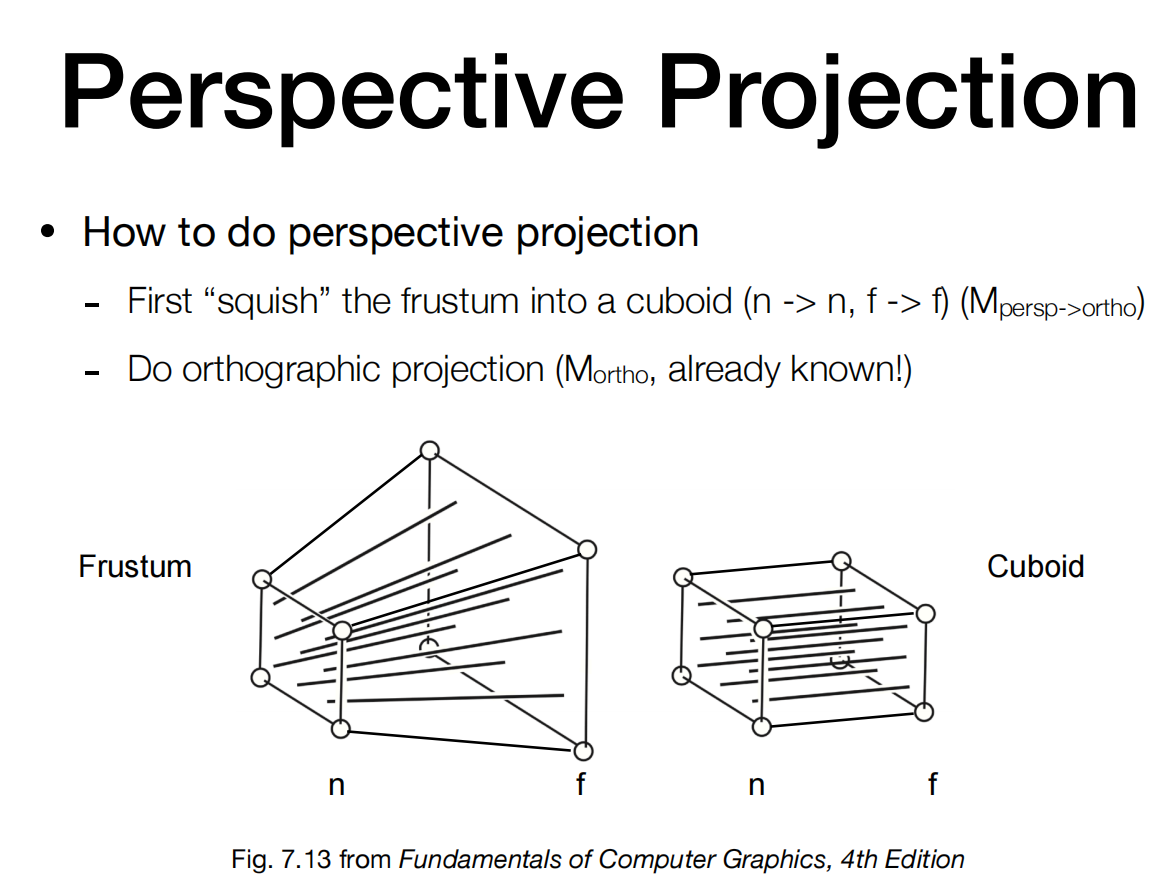
透视投影直接做或写出来比较困难。我们可以将远平面中间的位置，即这个Frustum（图形学中将远和近中间的区域叫做Frustum）从四棱竹的形状“挤”成立方体，然后再做正交投影即可。

在“挤”的过程中，要做一些规定：

最近的平面不能变
要“挤”的z轴上的值不会变化（只向自己平面内中间收缩）
远平面的中心点也不会发生变化

“挤压”矩阵

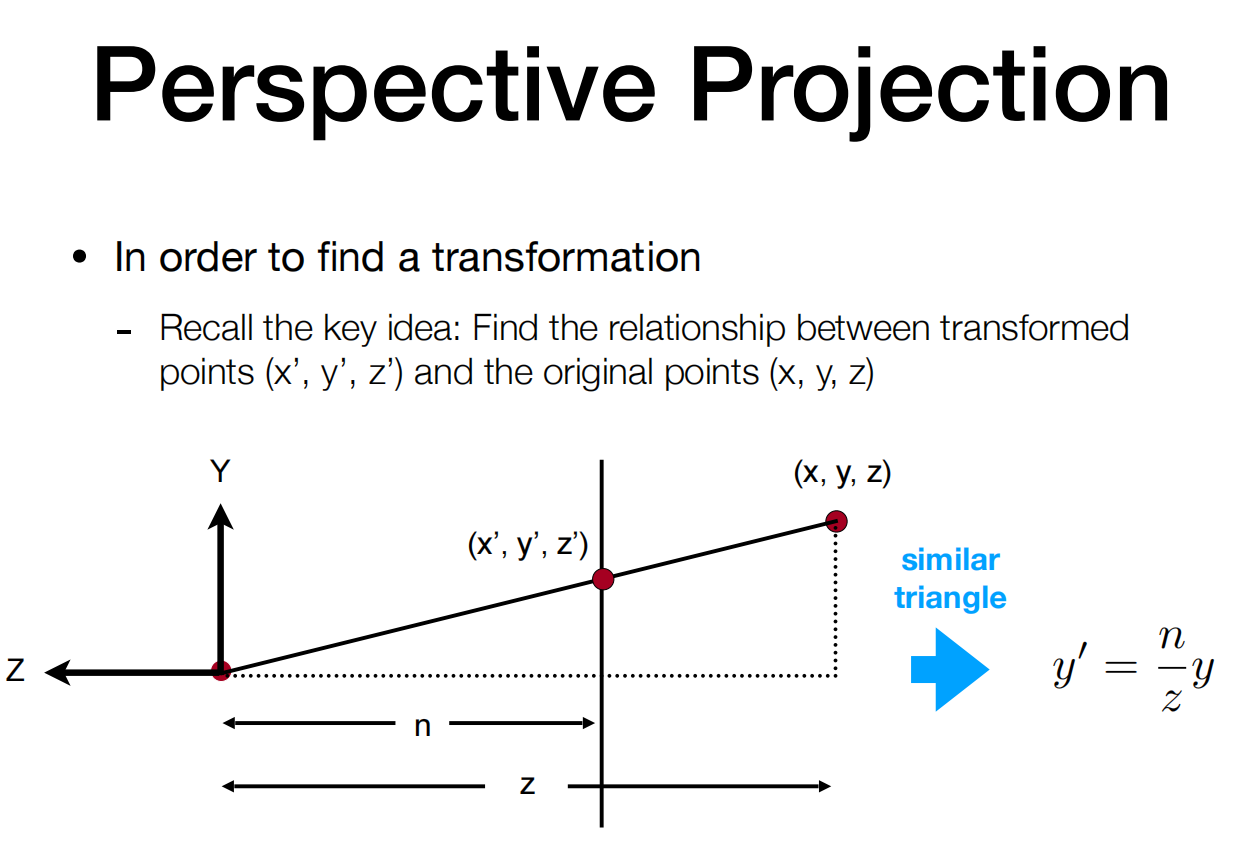
回忆一下关键思想：找出变换点(x’，y’，z’)和原始点(x，y，z)之间的关系

通过相似三角形，可以得到变换点和原始点之间的关系。

图中第一个式子就是变换点和原始点之间的关系。

图中第二个式子，是原始点到变换点的过程。(x,y,z,1)会被映射成最右边的向量。

矩阵推导

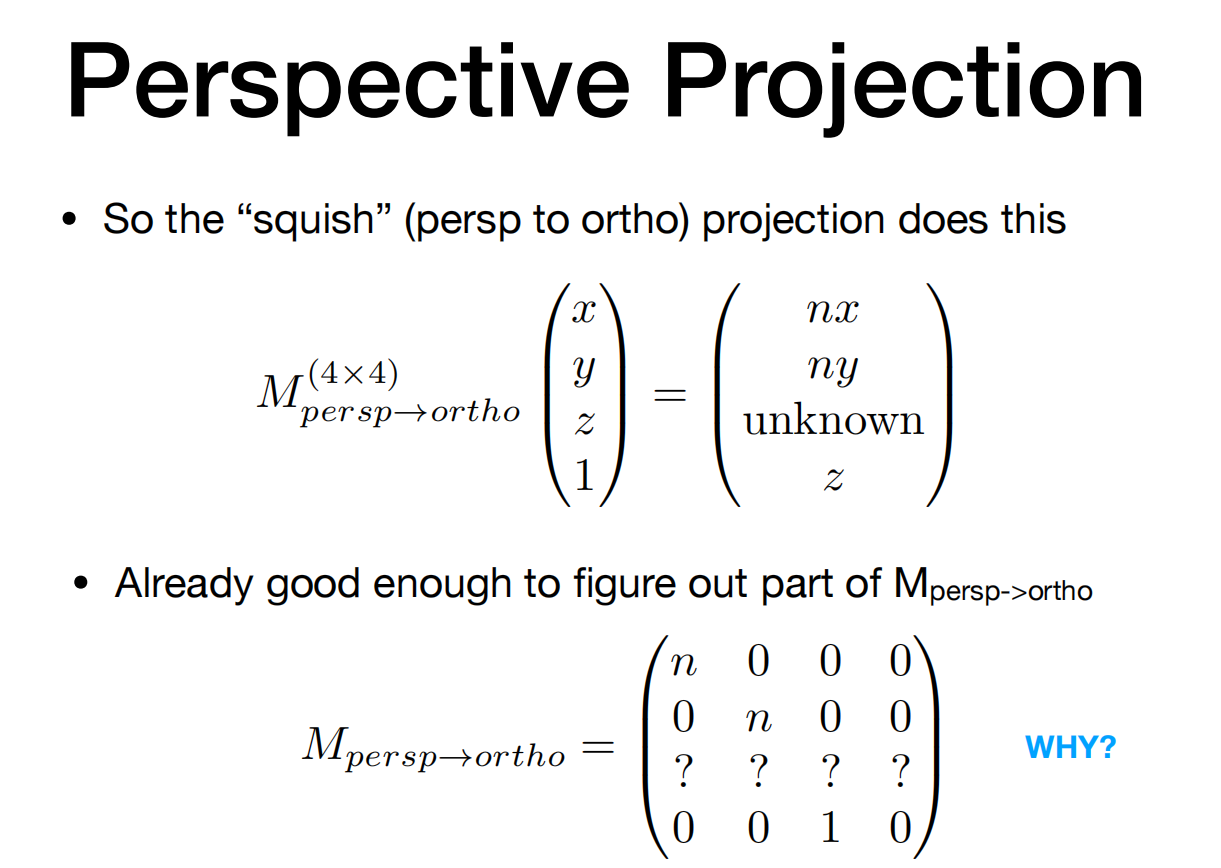
所以“挤压”(透视到正交)投影就是这样做的
可以找出部分的Mpersp->ortho

Mpersp->ortho就是挤压矩阵。

图中第一个式子表示，用挤压矩阵Mpersp->ortho乘以原始点就可以得到最后的变换点。原始点和变换点都部分已知，求出挤压矩阵即可。

图中第二个式子是求出的“挤压”矩阵（数学算出来的。。。）。第三行不知道，先放着。

矩阵第三行推导

这里的推导，emmmm怎么说呢，还是在用特殊值推导。了解下推导过程就好。。

如何求出图中矩阵的第三行 --有什么有用的信息吗
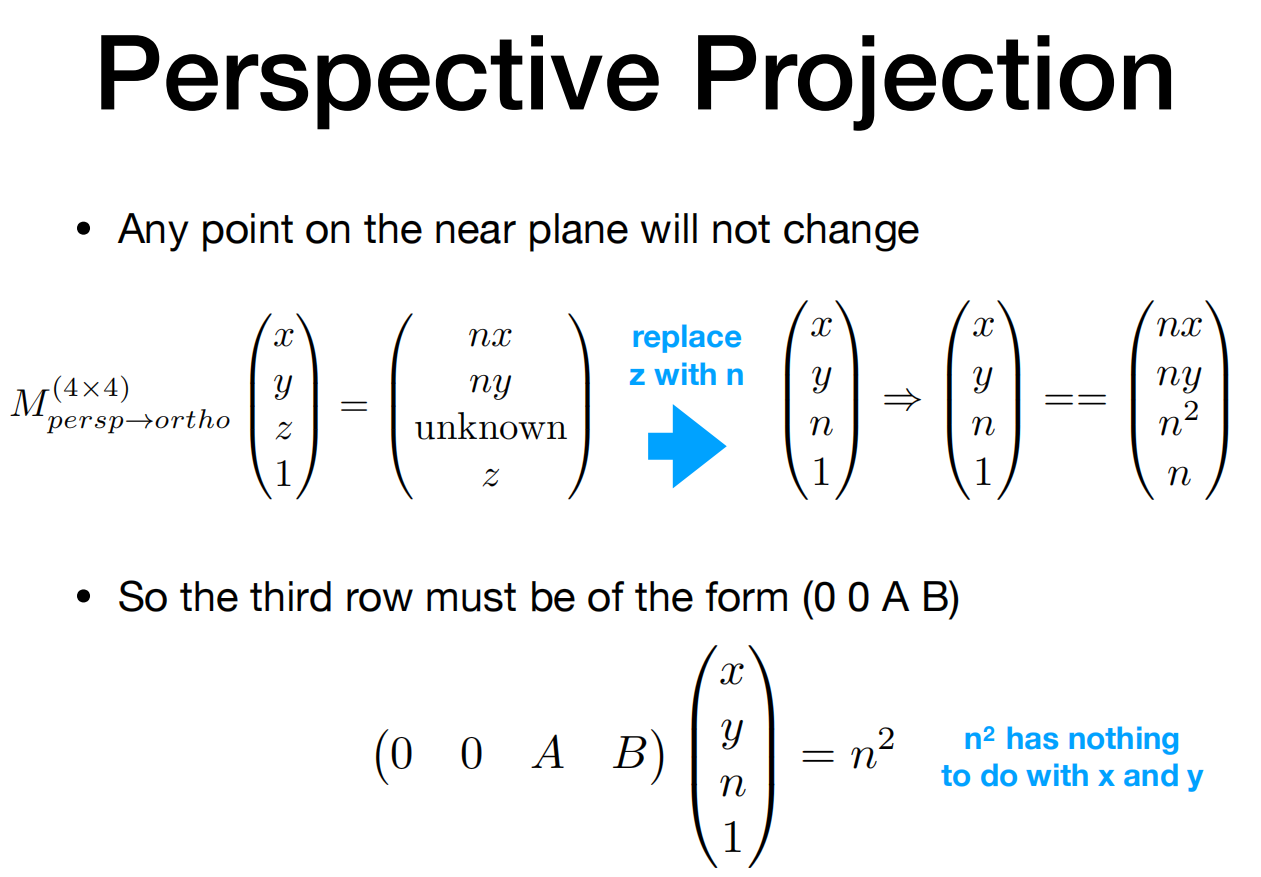
观察:第三排负责 --近平面上的任何点都不会改变 --远平面上的任何点的z都不会改变

信息1：近平面上的任何点都不会改变

近平面上的任何点都不会改变。用n代替z的值
所以第三行一定会是(0 0 A B)的形式 n2与任何x y 上的值都无关

n为近平面到摄像机的距离。

这里就是先让原始点的z值为n，然后x y值依旧不知道。此时就会变成：矩阵第三行(? ? ? ?) 乘以列矩阵(x,y,n,1) 等于n2。

即：?x+?y+?n+?=n2（矩阵的乘法，第i行分别乘以第i列的元素然后相加)

然后观察 ?x+?y+?n+1=n2 这个式子，等号右边没有出现任何的x y，那么他们的系数只能是0。第三四个系数还是不知道，设为A B。因此就有了(0 0 A B)这个东西，从而能得到 An+B=n2 这个式子。

信息2：远平面上的任何点的z都不会改变

和信息1一样，带入特殊值。f为近平面到摄像机的距离。

在信息1推导出的(0 0 A B)基础上，带入f，可以得到Af+B=f2

联立解方程

联立两个式子，用韦达定理解出了A B。此时就能够得到Mpersp->ortho“挤压”矩阵了。

透视矩阵

通过“挤压”投影得到“挤压”矩阵后。先“挤压”再正交投影，就可以得到透视矩阵。

总结

二维三维补充

今天先是对之前缩放、平移和旋转等这些变换在二维、三维上的一些补充。

二维

二维上是对旋转矩阵的补充。

求物体旋转-θ时的旋转矩阵，发现R-θ = Rθ-T
这里引出性质（理论上二维三维都通用）：在旋转里，旋转θ的旋转矩阵的转置等于旋转θ的旋转矩阵的逆。（数学上的正交矩阵）

三维

三维上时对缩放、平移和旋转变换的补充。

三维的缩放和平移变换很简单，原理和二维的一致。
三维的旋转变换，其会有绕x、y、z轴三个方向旋转的情况，对应的旋转矩阵都会不一样。
x和z的旋转矩阵分析方法一致。
绕y轴的旋转矩阵比较特殊，其值是x 、y的旋转矩阵的负值。这是因为在右手系下，x叉乘y是-z。
此外，还提及了四元数。由于矩阵不适合做差值，因此会用四元数。

观测变换

课上的重点是观测变换。观测变换有模型、视图、投影三种（简称MVP变换）

个人理解模型变换像是“建模”这种，这里就不需要讨论。

视图变换

视图变换的主要原因是摄像机的摆放问题，抽象上来看，就是坐标系的建立和转换的问题。

通过定义，我们规定了一套标准的坐标系。但是摄像机自身的坐标系并不一定与标准坐标系重合，这个时候我们需要进行坐标系的转换（视图变换）。
视图变换时，要将视图（定义的摄像机的前后上下，原点，在Y上，看-Z）坐标轴通过平移、旋转等变换回到标准坐标系上。
视图坐标的X轴是通过y和z叉乘得到，要将一个叉乘旋转比较麻烦。因此可以反过来，让标准坐标系旋转到视图坐标系上。接着通过前面的正交矩阵性质（在旋转里，旋转θ的旋转矩阵的转置等于旋转θ的旋转矩阵的逆），能够求出旋转矩阵。
平移矩阵很简单，直接是原点的移动就可以得到
视图变换是先旋转，再平移。通过旋转矩阵和平移矩阵，就可以算出视图矩阵。