数据的降维

为何要进行降维

在工作场景中，我们面对的数据通常是现实中直观观测的集合。这些数据可能多方面，多角度的描述了目标，因此根据这些数据我们可以很直观的了解观测的目标。可是我们在进行机器学习处理数据的时候，过多的数据即数据的维度过多可能会对算法性能有一定的影响或者造成不必要的浪费。例如你想判断一些人的性别，收集到的数据有年龄，身高，肤色，体重，发色等等。实际上肤色发色这种数据就是冗余的。

对于一个维度为d的数据局，大多数算法的复杂度为O(nd^2)，n为数据集中样本数量。所以当维度增长时，复杂度至少以平方增长，导致算法速度过慢。

而且维度增长对于算法的准确度也会有影响，假设我们在一维空间中对于十个点进行聚类。如果特征空间增长到二维，要想数据保持先前的数据密度，那么样本数量要提升到10^2=100个。依次类推n维需要10^n个样本才能到达之前的数据密度。

所以在保持尽量保存数据内所含信息的前提下进行数据的降维，是非常有必要的。

 

特征选择

如果部分特征的相关度高，容易消耗计算性能，而且有些维度是噪音，对预测结果有负影响。这个时候我们就可以进行特征选择，特征选择就是单纯地从提取到的所有特征中选择部分特征作为训练集特征， 特征在选择前和选择后可以改变值、也不改变值，但是选择后的特征维数肯 定比选择前小，毕竟我们只选择了其中的一部分特征。

一个最简单的方法就是删除低方差特征，直观来说低方差的特征对于样本没有很好的区分度，所以是不会造成很大影响的。不过缺点也很明显，这种方法虽然可以降维，但是直接把一整个维度所含的信息都丢掉了，丢失的信息有点多。那么我们可不可以把多个维度的信息减少到少数维度上呢。

 

PCA降维

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的，类似这种情况。

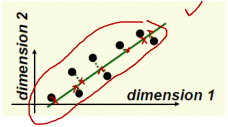
用这条新的直线为坐标轴便可以表示原来的两个坐标轴。这种情况看起来很像线性回归。但事实上他与线性回归还是有差异的。

如上所示，线性回归计算loss时是计算y值得差异，而PCA计算loss的时候是以点到直线的投影为差异的。

那么具体PCA是如何计算的呢，第一个新坐标轴选择是原始数据中方差最大的方向，即区分度最高的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推，可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0，即不包含任何信息。于是，我们可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

我们可以发现，新的坐标轴其实就是对于原先坐标轴的线性变换。这让我们想到了什么呢，就是矩阵。我们知道每一个矩阵都代表一种线性变换，而矩阵的相乘就是实现矩阵线性变换的过程。

事实上，通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值特征向量，选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中，实现数据特征的降维。

由于得到协方差矩阵的特征值特征向量有两种方法：特征值分解协方差矩阵、奇异值分解协方差矩阵，所以PCA算法有两种实现方法：基于特征值分解协方差矩阵实现PCA算法、基于SVD分解协方差矩阵实现PCA算法。具体过程大家有兴趣的可以自己推导，本文就不再赘述。