水下软体机器人的动力学建模

水下软体机器人的多软体动力学模型

1 引言

海洋作业和近海工业日益增长的需求要求水下机器人在愈发严苛的环境中执行越来越艰巨的任务。然而，某些海上场景所面临的挑战使得传统的遥控水下机器人（ROV）和自主水下航行器（AUV）可能难以胜任。解决这一问题的途径在于开发创新型水下机器人，这类机器人具备更强的机动性和灵活性，可满足海洋领域不断增长的需求。

近年来，水下机器人技术已从对生物启发式运动日益增长的兴趣中获益匪浅，因为水下机器人的设计可以

从对这些动物的游泳策略、流体动力学和生理学的研究中获益巨大。已有多 个以水生生物为灵感来源设计出可靠机器人对应物的例子。其中，鱼类的鳍 和尾部摆动（例如[1]）在科学界获得了最广泛的认可，部分原因在于对其 运动所涉及的基本物理原理已有较为深入的理解[2]。

复制驱动鱼类推进的驱动机制的设计标准在大多数情况下都涉及用有限 序列的刚性连杆和关节替代连续变形体，并减少自由度（DOF）的数量。然 而，最近[3]尝试通过采用连续柔性结构和执行器来考虑这些生物的柔顺特 性。这是少数几个将软体机器人设计原则应用于水下环境的例子之一。在水 中，由于缺乏刚性部件所带来的障碍被载体所浸没的稠密介质提供的支撑所 补偿，消除了软体机器人在陆地上面临的许多限制。这促使作者开发出一种 新型的水下软体机器人，其灵感来源于典型的软体海洋生物——章鱼。

尽管软体无人水下航行器（SUUVs）的设计可能相对简单，但其建模 与控制却远非直接明了。本文提出了首个绳索驱动、多体、水下软体机器人 的实例，并引入一种模型方法，该方法考虑了机器人平台的连续体特性，能 够描述该载体在静止流体中运动时的动力学行为。

1.1 一种水下多体软体机器人

章鱼具有一系列在水下机器人领域备受追捧的特征。这些特征主要包括游泳、 爬行和操作能力，以及整体上显著的结构柔顺性。这些特性使章鱼成为水下 航行器的理想范例。在海上作业场景中，复杂环境和扰动条件是常态，采用 软体/仿生方法的设计标准可能为当前无人水下航行器（UUVs）无法胜任的 广泛任务提供可行的解决方案。

作者受到章鱼的启发，开发出一种能够在水中行进并复制这种水生生物 某些显著技能的软体载体[5]。这项工作的成果在图1中以示意图形式展示。

该首个原型为一种水下多体软体机器人，其平台体积中有高达80%由类橡胶 材料构成，既可通过水中脉冲喷射推进，也可通过足式运动在水环境中进行 操作和移动。

该机器人主要由一个中央弹性壳体组成，此处称为软壳套膜（SSM），用于执 行脉冲喷射推进

脉冲喷射推进器，(2) 喷嘴， (3) 驱动壳体收缩的缆线，(4) 连续体机械臂，(5) 机械臂的执行器，(6) 壳体的执行器以及 (7) 驱动机械臂驱动的缆线)

一种用于水下软体机器人的多软体动力学模型 145

循环吸入与排出有限体积的周围水[6, 7]。从该中央单元延伸出多个机械臂， 即软体机器人手臂（SRAs）：这些是锥形连续结构，由弹性体材料制成， 旨在执行基本操作[8]和足式运动[9]。驱动完全通过缆线传动实现：不可伸 长缆线贯穿机械臂并位于中央壳体内，当从指定直流电机进行卷绕时，可驱 动机械臂的旋转或导致壳体坍塌。

组装完成后，航行器如图2a所示。该航行器已在受控环境和开放水域中进行了 测试，见图2b以及建模

PoseiDRONE在组装完成时(a)和海上测试期间(b))

146 F. 伦达等

对该复杂系统的建模与控制已通过分别考虑各个机械单元 [6, 10]来实现。

在此，作者首次尝试建立一个统一模型，以涵盖内部驱动和外部动力学。

2 机器人臂与软壳体部分模型

在几何精确方法中，SRA被视为柯瑟拉杆[11],，即刚性横截面的连续组合， 而SSM则被建模为柯瑟拉轴对称壳[12],，即沿中面的纤维连续组合。本节基 于作者先前的工作[8, 13],，简要描述水下软体机器人中柯瑟拉杆/壳体的运 动学与动力学，更详细的推导应参考该文献。模型的实验验证已在[8]中针对 SRA给出，而对于SSM，稳态实验已在[14],中呈现，动态实验正在审稿中， 耦合的动力学‐势流解在[15]中给出。为了体现两个模型之间的对称性，尽管 存在符号表示上的轻微滥用，我们有时会对两种模型方法采用相同的符号， 因为它们在两种情况下具有相同的几何和机械意义。

2.1 运动学

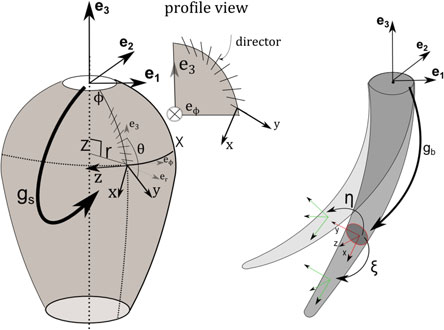
参考空间赋予了一组正交单位矢量基 (e1,e2,e3)（图3）。在Cosserat理论中， 某一时刻软体的构型由位置矢量u和材料取向矩阵R表征，其参数化为‐

一种用于水下软体机器人的多软体动力学模型 147

由材料的弧长坐标参数化，其中 φ ∈[0, 2π[,为轴对称曲面的旋转角度，X ∈[0,Ls]为SSM沿子午线的弧长坐标；X ∈[0,Lb]为SRA中机器人臂的弧长 坐标（下标s和 b分别代表壳体和梁）。因此，构型空间定义为曲线gb(X)和 曲面gs(X, φ) ∈SE(3)，其中gb=(Rb b 0 1) r且gs=(Rs s 0 1) r。

为了利用SSM的轴对称性，我们引入另一个固定在材料点(X, φ)上的正交基： (er, eφ, e3)（图3）；该正交基由g1(X, φ)的(e1, e2, e3)旋转‐平移得到，等于：g 1=(exp(˜ s 0 1) 3φ e ) r ，其中exp为SO(3)中的指数映射。在此情况下，rs(X ) 的形式为：rs=(cos(φ)r, sin(φ)r, z)T，其中r(X ) 和z(X ) 是两个光滑函数，分 别定义点X在轮廓上的半径和高度（图3）。为方便起见，我们引入另一个由前 一个正交基通过g2=(exp(˜erπ 0 0 1) 2 / ) 旋转得到的正交基(er, e3,−eφ)。然后， 若记 θ(X ) 为e3与位于 φ‐子午线任意X处的壳体纤维之间的夹角，则所谓的方向 正交框架(x, y, z)在每一时刻t由g3(X ) 定义为：g3=(exp(−˜ 0 0 1) φθ e ) 。最后， 将所有这些组合起来，壳体构型空间为gs= g1g2g3。

̂现在，沿曲线 gb(X ) 的切向量场定义为 ξ(X ) =g−1b ∂gb/∂X =g−1b g′ b ∈se(3)，曲面 gs(X, φ) 上的切平面由以下两个向量场定义：ξ̂1(X) =g−1 s ∂gs/∂ X = g−1 s g′ s 和 ξ̂2(X ) =g−1 s ∂gs/∂(rφ) = g−1 s g s（其中 表示参考构型中的变量）。 在局部坐标系分量中，我们有： ξ=(kT, gT)T, ξ1=(kT 1, gT 1)T=(0, 0, μ, λ, β, 0)T,ξ2=(kT 2, gT 2)T=( sin(θ)r , cos(θ)r , 0, 0, 0,− rr) T ∈R6。其中 g(X ) 表示线 应变，k(X) 表示角应变。帽子算子是扭转向量空间 R6 与李代数 se(3) 之间的同 构。

构型曲线gb和曲面gs的时间演化由扭转向量场 η(X) ∈ R 6分别表示为 ̂ηb= g−1 b ∂gb/∂t = g−1 b ˙gb和 ̂ηs= g−1 s ∂gs/∂t = g−1 s ˙gs。与之前一样， 在局部分量中有： ηb=(wT b, vT b)T, ηs=(wT s, vT s)T=(0, 0,Ω, Vx, Vy, 0)T ∈ R6,，其中v(X)和w(X)分别为某一时刻物质元的线速度和角速度。

根据该运动学，SRA和SSM的状态向量由三元组(gb, ξ, ηb)和(gs, ξ1, ηs)表 示。由上述推导可得运动学方程(1)和(2)，而在接下来的章节中将推导相容 性方程和动力学方程（波浪号表示R 3中的向量与其对应的反对称矩阵之间 的同构∈因此(3)）。

r˙b= Rbvb
R˙b= Rbw˜b. (1)

148 F. 伦达等

θ˙= Ω
r˙= cos(θ)Vx − sin(θ)Vy
z˙= sin(θ)Vx+ cos(θ)Vy
(2)

2.2 应变度量

对于连续介质的应变测量有多种方法，我们分别选择在梁和壳体的专业文献中最常 用的方法。

对于SRA，应变定义为变形构型 ξ与参考构型 ξ之间的差异。特别地， k −k的分量度量了扭转以及两个方向上的弯曲状态。类似地，g −g的分 量表示纵向应变（伸长、压缩）和两个剪切应变。

对于SSM，根据[12]所述，描述中面内膜应变状态的应变张量场为 e(X) = 1/2(h −h)，其中h(X)是Reissner壳体的第一基本形式，等于h = diag(λ2+ β2, r 2/r 2)。因此我们有e =(1/2) ∗diag(λ2+ β2 −1, r2/r 2 −1)， 其中我们定义了h 11= 1。关于剪切应变状态，我们有s(X) = β − β。最后， 弯曲应变状态由张量场d(X) =k −k,参数化，其中k(X)是第二基本形式， 等于k =diag(−μλ,−r sin(θ)/r2)。因此我们有d =diag(μ − μλ, sin(θ)/ r −r sin(θ)/r2)。此外，自然地认为在参考静止构型中不存在横向剪切， 即 β= 0。

2.3 相容性方程

我们之前已经看到，g′ b=gbξ 和 g′ s=gsξ1。对这些方程关于时间求导， 并注意到 ˙g=ĝη，我们得到速度与变形变量之间的如下相容性方程： ˙ ˙ξ= η′ b+ adξ(ηb) 和 ξ1= η′ s+ adξ 1(ηs)，其中 ad 是伴随 映射。在局部坐标分量中，我们得到：

g˙= v′ b+ k× vb −wb × g
k˙= w′ b+ k× wb
(3)

μ˙= Ω′
λ˙= V′ x+ βΩ − μVy
β˙= V′ y − λΩ+ μVx
(4)

一种用于水下软体机器人的多软体动力学模型 149

2.4 动力学

描述里斯纳杆和壳体（不一定为轴对称）演化过程的偏微分方程已在[11] 和[12]中分别推导得出。相对于局部参考系，这些偏微分方程可用几何符号 表示为：Mb η˙b=F b′i+ad∗ ξ(Fbi) +Fbe −ad∗ ηb(Mbηb) 和 Ms η˙s= 1/j ( jF s1i)′+ ad∗ ξα(F sαi) +Fse −ad∗ ηs(Msηs)，其中 j =√det(h) =r/r√λ2+ β2,Fbi(X ) 和 F sαi(X ) 是由gα(α取值于{1, 2})所给定的表面方向上的内力力旋量，Fbe (X) 和 Fse(X) 是分布载荷的外力旋量，Mb(X) 和 Ms(X) 分别为螺旋惯性矩阵， ad∗= −adT为余伴随映射。对于重复指标 α，应采用爱因斯坦求和约定， 如同本文其余部分一样。现分别明确内力和外力旋量的角分量和线性分量 （轴对称情况见[16]）：Fbi=(MT b, NT b)T，F s1i=(M1T s, N1T s)T=(0, 0, MX, NX, H, 0)T，F s2i=(M2T s, N2T s)T=(Mφx, Mφy, 0, 0, 0,−Nφ)T ∈R6,，以及 F be=(mT bn T s, nT s)T=(0, 0, l, fx, fy, 0)T ∈R6,，其中N(X)和 M(X)分别为内力和力矩向量，而n(X)和m(X)分别为单位X上的外力和力矩。

螺旋惯性矩阵为：Mb= ρb ∗diag(Ib, Jb, Jb, A, A, A) 和 Ms= ρs ∗diag(Js, Is, Js, 2hs, 2hs, 2hs) ∈R 6 × R6。在上述方程中， ρb和 ρs为体密度，A(X)为截 面面积，且A = πh2 b，其中hb(X )为横截面半径，hs为壳体厚度的一半， J(X)、I(X)为微固体的惯性二阶矩，其表达式为Jb= πh4 b/4，Js= h2 s/3，I b= πh4 b/2，Is ∼ 0。动量方程在各分量形式下为：

ρbAv˙b= N′ b+ k× Nb+ nb −wb × ρbAvb
ρbJb w˙b= M′ b+ k× Mb+ g× Nb+ mb −wb × ρbJbwb
(5)

ρs Js Ω˙= 1/j(j MX)′+ λH − βNX − cos(θ) r Mφ x+ sin(θ) r Mφ y+ l
2ρshs V˙x= 1/j(j NX)′ − μH − cos(θ) r Nφ+ f x+ 2ρshsΩ Vy
2ρshs V˙y= 1/j(j H)′+ μNX+ sin(θ) r Nφ+ f y −2ρshsΩ Vx
(6)

其中 Jb等于diag(Ib, Jb, Jb)。

2.5 本构方程

基于Kelvin‐Voigt模型的线性粘弹性本构方程被选用。在[8]和[13]中我们分别 得到：

Fbi= (ξ − ξ )+Υ(ξ˙),
(7)

150 F. 伦达等

NX= 2Ehs 1−ν2[λ(e11+ νe22) − Jsμ(d11+ νd22)] + 6υhs 1−ν2[λ(e˙11+ νe˙22) − Jsμ(d˙11+ ν d˙22)]
Nφ= 2Ehs 1−ν2[ r r(e22+ νe11) − Js sin(θ) r(d22+ νd11)] + 6υhs 1−ν2[ r r(e˙22+ νe˙11) − Js sin(θ) r(d˙22+ ν d˙11)]
H= 2hsβ[G+ E 1−ν2(e11+ νe22)]+ 2hs β˙[υ+ 3υ 1−ν2(e˙11+ νe˙22)]
MX= −2Ehs Js 1−ν2 λ(d11+ νd22) − 6υhs Js 1−ν2 λ(d˙11+ ν d˙22)
Mφx= −2Ehs Js 1−ν2 r 1−ν2 r
Mφy= 0
(8)

其中 (X)和 Υ(X) ∈R6 ⊗R6分别为螺旋刚度矩阵和螺旋粘度矩阵，等于= diag(重力向量G Ib, 杨氏模量 Jb, 杨氏模量 JB, 杨氏模量 A, 剪切模量 A, 剪切模量 A)，Υ= υ ∗diag (Ib, 3Jb, 3Jb, 3A, A, A)，其中E为杨氏模量，G为剪切模量 （对于具有泊松比 ν的各向同性材料，G = E/2(1+ ν)）， υ为剪切粘度模量。

2.6 外部载荷

考虑到的外部载荷包括流体施加的力（即阻力、附加质量、浮力和推力）以 及重力载荷。数学上我们有：

nb= grb+ bb+ db+ ab
(9)

ns= ds+ as+ ts
(10)

其中，grb(X)是重力向量g_r，bb(X)是浮力，ts(X)是推力载荷，d(X)是阻力，a(X) 是附加质量。

基于通常施加在刚性火箭上的合外力模型，并均匀“涂抹”在软体部分 上，目前正在进行对SSM流体作用力模型的详尽推导与解释。此处仅报告最 终方程，因其不影响本工作的范围。对于SRA，流体作用力模型最初在[17] 中推导得出，随后在软体机器人背景下引入于[8]。

重力和浮力分别是机器人臂X单位长度的质量 ρb与水 ρw的质量，乘以 重力加速度gr=−9。81：grb+ bb=(ρb − ρw)AR T b G，其中G为重力加速度 向量，等于G=(0,0, gr) T。

阻力载荷矢量与速度矢量的平方成正比，且方向相反。阻力载荷的幅值 还由截面几何形状X以及由经验系数表示的水动力现象决定。对于SRA和 SSM，分别有：db= −ρwv T bvbD v b |
一种用于水下软体机器人的多软体动力学模型 151

以及 ds=RsT(0, 0,−ρwCdAref | 2 | V V Am)T，其中 D(X ) ∈R3 ⊗R3 对于半径 力学系数；Aref 是参考面积，等于π(max(r (X )))，A2, 是 SSM 的总表面 面积，Cm 是净阻力系数。V 是在每个时间步长计算的游动速度，即标量场 d z(X ) 的平均值，即 V ˙(1/A=) mo ∫ Lsz( ∫ 2π 0 ˙z−)d Xr′d。

附加质量载荷矢量与加速度矢量成正比，且方向相反。其幅值还由截面 X的几何形状以及通过修正系数部分表达的水动力现象决定。对于SRA和 SSM，分别有：ab= −d(ρwFvb) dt =−ρwF˙vb −wb × ρwFvb和as= −Bsρs2hs˙ vs= −Bsρs2hs( ˙Vx, ˙Vy, 0)T，其中Bs为净附加质量系数，F(X) ∈ R3 ⊗ R3 是一个张量，包含了几何和流体力学因素，等于F = diag(0, ABb, ABb)， Bb为流体力学修正系数。

推力载荷为：ts=R T s(0,0,−ρw ˙U| ˙U| AnAm)T，其中An为喷嘴面积，在出流时 等于An= πh2 n，在入流时等于An= 3πh2 n（使用了三个入口和一个出口，半径为 hn），而U为外套腔内部体积。

2.7 内部驱动

为了驱动SRA和SSM，我们施加一个内部分布力旋量（Fa(X,t)），其代表模 型输入。该力旋量可被视为生物体体内肌肉纤维的作用，或如[8]中所述的嵌 入式绳索驱动的结果。最终的动力学方程如下：Mb η˙=F ′ bi+ad∗ ξ(Fbi) +F ba+Fbe −ad∗ η(Mbη) 和 MS η˙= 1/j ( jF s1i) ′+ad∗ ξα( F sαi) +Fsa+Fse −ad ∗ η(Mbη)。

3 多软体动力学模型

为了对如图1所示的SUUV的行为进行建模和控制，需要一种将SRAs和 SSMs连接在一起的方法。本节展示了柔性体在星形构型（即具有移动基座 的树状结构）中的连接方式，接着讨论了由于整体运动引起的柔性体外部载 荷的更新，最后建立了系统的整体动力学模型。

152 F. 伦达等

为欧几里得固定坐标系，(e 1,e2,e3)表示刚体和柔性体参考坐标系，而(x,y,z)是 μ个 固体的局部坐标系)

3.1 星型系统运动学

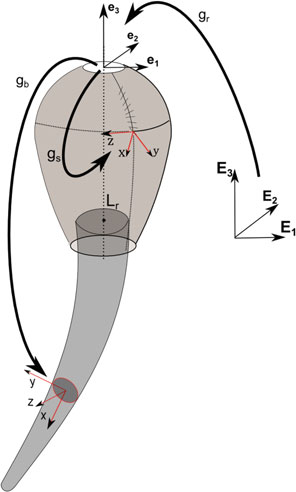
为了将柔性体以星形构型连接，可以将一个集束刚体（GRB）与已引入的坐 标系（e1,e2,e3）配对。设（E1,E2,E3）为欧几里得固定坐标系，则GRB的构 型空间定义为一点gr ∈SE(3)，将（E1, E2, E3）映射到（e1, e2, e3）中（图4）， 其中gr=(Rr r 0 1) r。

gr的时间演化由扭转向量 ηr ∈R 6表示，定义为̂ηr= g−1 r ˙gr。根据该运 动学，GRB的状态向量由对(gr, ηr)给出，由此可直接得到运动学方程：

g˙r= gr̂ηr
(11)

此时，SUUV各点的构型由g= grg(s,b)给出，如图4所示。值得注意的是， 在该方案中，柔性体的数量、几何形状和相对位置可以任意选择。实际上， 在本示例中，我们通过向rb的第三个元素添加 −Lr（即GRB的长度），在 SSM和SRA之间施加一个刚性平移L（如图4所示）。

一种用于水下软体机器人的多软体动力学模型 153

3.2 外部载荷更新

为了考虑整体运动，在每个时间步长中，利用GRB的状态向量（gr, ηr）来计 算柔性体的外部载荷实际值（10）、（9）。在本例中，我们将参考系RrT中 的重力向量G旋转，得到如下新方程：grb+ bb=(ρb − ρw)ART b R rT G。随后， 我们通过分别添加标量Vr=(0, 0, 0, 0, 0, 1)ηr（即GRB在游动方向e3上的线 速度）和向量 ¯vr= diag(0, 0, 0, 1, 1, 1)Adg−1 b ηr（即GRB的线速度在局部 参考系(x, y, z)中的传递），更新了游动速度V和线速度vb，其中Ad为伴随 矩阵。SRA和SSM的新的拖曳载荷方程变为：db= p g q −ρw(vb+ v¯r)T(vb+ v¯r)D vb+ v¯r ∣ and ds= R T s(0, 0,−ρwCd Aref(V+Vr)|V+Vr| 2Am )T.

3.3 星系系统动力学

此时，为了获得软体无人水下航行器的动力学模型，我们仅缺少集总刚体的 动力学，该集总刚体用于收集柔性附件。在几何表示法中，可将其写为：

Mr η˙r= Fr − ad∗ ηr (Mrηr)
(12)

由GRB汇集的软体无人水下航行器（SUUV）的柔性体在其当前形状下被冻 结。利用这一点，上述未知参数（Mr, Fr）可按如下方式计算（[18]）：M r= ∫ 2π 0 ∫ L s 0 Ad∗ gs MsAdg −1 s(−z′)d Xrdφ+∫ L b 0 Ad∗ gb MbAdg −1b d X +Mri= M ′ s+M ′ b+Mri，以及Fr=∫ 2π 0 ∫ L s 0 Ad∗ gs Fse(−z′) d Xrdφ+ ∫ L b 0 Ad∗ gb Fbe√gT gd X +Fre=F ′ se+F ′ be+Fre，其中Mri和Fre分别为直接属于GRB的固有惯 性和外部载荷，Ad∗ g=(Adg) −T为余伴随映射。值得注意的是，由于考虑的 是冻结形状，柔性体的内部反作用力和驱动不参与这些积分。此外，作为一 阶近似，未计入柔性体相对加速度引起的惯性载荷。柔性体的附加质量载荷 在F′ se和F′ be中的贡献将表现为额外质量，如下所示：M ′ sa= Bsρs2h ∫ 2π 0 ∫ L s 0 Ad∗ gs 对角矩阵diag(0,0,0,1,1,1)Adg −1 s(−z ′ )d Xrdφ，以及M ′ ba=BbρwA ∫ L b 0 Ad∗ gb 对角矩阵diag(0,0,0,0,1,1)Adg −1b d X。

接下来详细说明，在本例中，GRB的固有惯性等于Mri= ρrUr(diag(Jr, Jr, Ir) ˜ u ˜u Tdiag(1, 1, 1) )，其中u =(0, 0,−3Lr/4) T是GRB质心相对于参考系(e1, e2, e3) 的位置矢量u；Jr、Ir为惯性二次矩，其值分别为Jr= 3(h 2 r /4+ Lr)/5和Ir= 3h2 /10 （选择的是底面半径为hr的圆锥形状）， ρr为密度 154 F. 伦达等 且Ur是等于Ur= πh2rLr/3的刚体体积。另一方面，所考虑的作用在GRB上的 外部载荷包括刚体的重力和浮力，以及SSM的重力和浮力，因为后者在轴对 称模型中尚未被计入。因此我们有：Fre=[(1 − ρw/ρr)Mri+(1 − ρw/ρs)M s′] Adg−1 r(0,0,0,GT)T.

3.4 软体无人水下航行器动态模型

最终的方程组由柔性体的二阶偏微分方程和星型系统的常微分方程组成。偏 微分方程组包括运动学方程(2)、(1)，相容性方程(4)、(3)以及动力学方程 (6)、(5)，并分别结合内应力(8)、(7)和外部载荷(10)、(9)进行补充。星型系 统的常微分方程组由运动学方程(11)和动力学方程(12)组成。最后，在状态 形式 ˙x = f (x, x′, x′′,t)下，SUUV模型为：

θ˙= Ω
r˙= cos(θ)Vx − sin(θ)Vy
z˙= sin(θ)Vx+ cos(θ)Vy
r˙b= Rbvb
R˙b= Rbw˜b
g˙r= gr̂ηr
μ˙= Ω′
λ˙= V′ x+ βΩ − μVy
β˙= V′ y − λΩ+ μVx
k˙= w′ b+ k× wb
g˙= v′ b+ k× vb −wb × g
Ω˙=[(j MX)′/j+ λH − βNX − cos(θ)Mφ/r ]/(ρJs)
V˙x=[(j NX)′/j − μH − cos(θ)Nφ/r+ 2ρshsΩ Vy+ f x]/[2hsρs(1+ Bs)]
V˙y=[(j H)′/j+ μNX+ sin(θ)Nφ/r −2ρshsΩ Vx+ f y]/[2hsρs(1+ Bs)]
v˙b=(N′ b+ k× Nb+ nb −wb × ρbAvb)/(ρbA)
w˙b=(J −1 b/ρb)(M ′ b+ k× Mb+ g× Nb+ mb −wb × ρbJbwb)
η˙r= M −1 r[Fr − ad∗ η r (Mrηr)]
(13)

最终系统是无限维的，因为其所有分量都是轮廓横坐标X的某些函数。因此， 为了进行数值求解，必须首先在节点网格上进行空间离散化，然后从初始状 态开始使用显式或隐式时间积分器进行时间积分。在此网格中，偏微分方程 组中出现的所有空间导数均可通过有限差分格式进行近似，边界条件为： η (0)= 0和Fbi(Lb)= F 1 si( Ls)= 0。这些操作已在Matlab©中实现。

一种用于水下软体机器人的多软体动力学模型 155

4 结果

尽管本研究的最终目标是建模和控制如图1所示的软体无人水下航行器，且 需要进行实验对比（如已分别对SRA [8]和SSM [14]所进行的实验），但在 本节中，基于上述建立的模型方法，通过仿真的示例说明来展示所提出数学 框架实现目标的可行性。进一步的仿真分析以及与真实样机的实验对比将在 本文的后续工作中展开。最后，通过当前模型方法进行能量分析，并用于描 述结果。

4.1 仿真

使用了一个SRA和一个SSM，前者为锥形，半径从max(hb(X)) = 15线性减 小至min(hb(X)) = 6mm；后者为半径31 mm的半球与长度86 mm的圆柱 体粘接而成，两者厚度均为hs= 1mm。GRB也呈锥形，底面半径为hr= max(hb(X)) = 15mm，高度为Lr= 112mm。这些结构体的密度被设定为 与水相同（1022[kg/m3]），使整体结构在水下保持中性浮力。几何和机械 参数总结于表1。

为了重现软体部分的喷射推进，SSM 通过一个垂直于对称轴（即沿 er 方向）的三角波力函数 fs(X, t) 进行驱动，其周期为 T，幅值范围在区间 [ Fmin, Fmax] 内。该压力施加在高度为 80 mm 的中心条带区域，以模拟机器 人臂的弯曲/转向能力；SRA 则通过一个线性力矩函数 fb(X, t) 进行驱动，其 极值为 [Mmin, Mmax]，在某一时间段 Δt1 内指向局部 z 轴方向，在另一时 间段 Δt3, 内指向 y 方向，前后分别有一个静止期，时长分别为 Δt2 和 Δt4。 换句话说，内部分布力旋量 Fsa(X, t) 的形式为：Fsa=Ad∗g−1 3(0, 0, 0, fs, 0, 0)T，而内部分布力旋量 Fba(X, t) 在每个时间段 Δt1,Δt2, Δt3, Δt4, 分别 具有不同的形式：Fba=(0, 0, fb, 0, 0, 0)T，Fba=(0, 0, 0, 0, 0, 0)T，Fba= (0, fb, 0, 0, 0, 0)T，Fba=(0, 0, 0, 0, 0, 0)T。载荷与动力学

表1 SUUV的几何和机械参数
	E(kPa)	(Pa ∗s)	ν(−)	ρ(kg/m3 )	L(mm)	h(mm)	hn(mm)
SSM	40	500	0	1022	130	1	10
SRA	110	300	0	1022	420	[6, 15]	–
GRB	–	–	–	1022	112	15	–

156 F. 伦达等

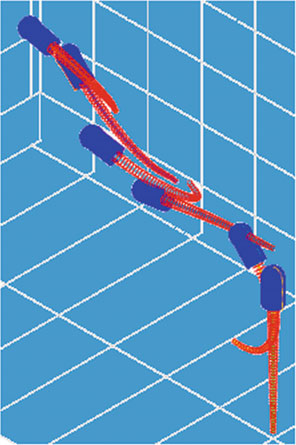
参数总结在表2中，而游泳动力建模结果的几个快照如图5所示。

尽管采用了简单的驱动模式，但由于流固耦合效应，在壳体幔层的弯曲 切换过程中产生的扭转力矩导致其绕对称轴出现意想不到的转动（e3），从 而呈现出复杂的游动动力学行为。这进一步表明有必要建立水下软体无人航 行器动力学的恰当模型，以便能够理解、设计和控制这些具有前景的水下探 索装置。

4.2 能量分析

任何类型的运动都是身体变形与环境[19]之间动态相互作用的结果。这种相 互作用的质量可以通过计算内部驱动功率如何转化为星型系统的动能功率来 衡量。在本研究中，内部驱动功率通过应力功率的正值部分进行近似，这表 明弹性能量主要来源于该作用，并且在此处仅能由内部驱动增加。利用这一 定量指标，可以在设计阶段调整几何、机械和驱动参数，以找到特定应用的 最佳方案。这可能是该模型的关键应用之一。

为此，我们在整个仿真过程中每个时间步长使用以下效率指标 E(t): E = WoWi，其中 Wo(t)和 Wi(t)分别表示星系统的输出动能和输入驱动功率。 Ls 2π计算它们，我们得到：Wo= ηT r Mr η˙r 和 Wi= Wis+Wib= ∫ ∫0 0 { 2Eh s z′)dX_r dφ+ L b ∫ 0 (ξ − ξ)T ξ˙√gTgdX，其中Wis(t)和Wib(t)分别为SSM和SRA的驱动贡献 （等于内部弹性能量的正值部分，其他情况下为零），且我们定义了E11= e11+ νe22,E22= e22+ νe11, D11= d11+ νd22和D22= d22+ νd11。在图6中， 显示了对应于图5仿真的驱动功率和动能功率。指标E的平均值约为3%。

在图6中可以识别出图5运动的5的不同阶段。在第一部分（Δt1）中，输 入功率由SSM的周期性收缩和SRA的弯曲组成。在第二阶段（Δt2）中，输 出动能得益于SRA释放的弹性能量以及新构型的正向增益，从而与驱动功率 相比产生更大差距。在第三部分（Δt3）中，由于新的弯曲，驱动功率增加， 而在最后阶段

一种用于水下软体机器人的多软体动力学模型 157

Table 2 Loading and dynamic parameters of the SUUV Fmin, Fmax	Mmin, Mmax	B(−)	Cd(−)	C(x,y,z)(−)
SSM	[0, 5]	T(s)		(Δt1,Δt2,Δt3,Δt4)(s)
		0.66	–	–
SRA	–	–	[0, 0.05]	(1.5, 3, 1.5, 3)

158 F. 伦达等

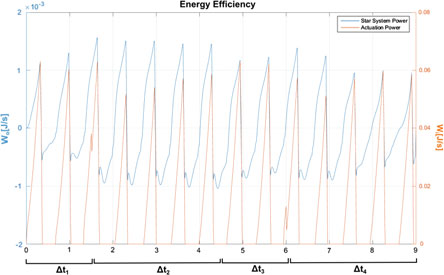
(Δt4) 由于弯曲的SRA存在流体动力耦合，软体无人水下航行器开始绕自身旋转， 其效率不如第二阶段的向前推进，导致动能与驱动功率之间的差距较小。

5 结论

一种考虑多软体机器人连续体特性的统一模型已被提出，该模型可用于描述 水下航行器在静止流体中运动时的动力学行为。通过一个示例对该模型的潜 力进行了验证，结果展示了复杂的和意想不到的 尽管存在常规的驱动输入，该机器人的动力学行为仍十分丰富且控制具有挑 战性。此外，提出了一种考虑内部驱动和载体机械性能的能量分析方法。本 文所展示的工作是开发用于智能软体无人水下航行器设计与控制的数学工具 的第一步。