《趣题学算法》Chapter 0 从这里开始

最新推荐文章于 2021-09-04 14:11:27 发布

人民邮电出版社有限公司

最新推荐文章于 2021-09-04 14:11:27 发布

阅读量253

点赞数

分类专栏：趣题学算法

本文链接：https://blog.csdn.net/rmyd01/article/details/118604675

版权

趣题学算法专栏收录该内容

13 篇文章 0 订阅 ¥44.16 ¥99.00

订阅专栏

Chapter 0　从这里开始

0.1　App程序与算法

0.2　计算问题

0.3　算法的伪代码描述

0.4　算法的正确性

0.5　算法分析

0.6　算法运行时间的渐近表示

0.7　算法的程序实现

0.8　从这里开始

0.1　App程序与算法

信息时代，人们时刻都在利用各种App解决生活、工作中的问题，或获取各种服务。早晨，手机里设定的闹钟铃声（或你喜欢的音乐）将你唤醒。来到餐厅，你用手中的IC卡到取餐处的刷卡机上支付美味早餐的费用。上班途中，打开手机上的音乐播放器，用美妙的乐声，打发掉挤在公交车上的乏味的时间。上班时，利用计算机中的各种办公软件处理繁忙的业务。闲暇时，你用平板电脑里的视频程序看一部热映的大片，或在淘宝网上选购你喜欢的宝贝。晚间，你用QQ或Facetime与远方的朋友聊天、交流情感……凡此种种，不一而是。

五彩缤纷的App后面是什么？这些神奇的体验是怎么创造出来的？如果你对这样的问题感兴趣的话，我们就成为朋友了。从这里开始，我们将探索创造App——计算机（及网络）应用程序的基本原理和基本技能。

其实，能用计算机（包括各种平板电脑、智能手机）解决的是所谓的“计算问题”，也就是有明确的输入与输出数据的问题。解决计算问题就是用一系列基本的数据操作（算术运算、逻辑运算、数据存储等）将输入数据转换成正确的输出数据。能达到这一目标的操作序列称为解决这一计算问题的“算法”。App就是在一定的计算机平台（计算机设备及其配备的操作系统）上，用这个计算机系统能识别的语言来实现算法的程序。

因此，对上述的第一个问题，我们的答案是：App背后的是算法。算法是解决计算问题的方案。要用计算机来解决应用问题，首先要能将该问题描述成计算问题——即明确该问题的输入与输出数据。只有正确、明白地描述出计算问题，才有可能给出解决该问题的算法。作为起点，本书并不着眼于如何将一个实际的应用形式化地描述为一个计算问题，而是向你描述一些有趣的计算问题，并研究、讨论如何正确、有效地解决这些问题。通过对这些问题的解决，使我们对日常面对的那些App有着更清醒、更理智的认识。可能的话，也许哪一天你也能为你自己，或者朋友、爱人创造出你和他们喜欢的App。

0.2　计算问题

上面已经说到什么是计算问题，下面就来看一个有趣的计算问题。

问题0-1　计算逆序数

问题描述

这个学期Amy开始学习一门重要课程——线性代数。学到行列式的时候，每次遇到对给定的序列计算其逆序数，她都觉得是个很闹心的事。所以，她央求她的好朋友Ray为她写一段程序，用来解决这样的问题。作为回报，她答应在周末舞会上让Ray成为她的伦巴舞舞伴。所谓序列A的逆序数，指的是序列中满足i<j，A[i]>A[j]的所有二元组<i, j>的个数。

输入

输入文件包含若干个测试案例。每个案例的第一行仅含一个表示序列中元素个数的整数N（1 $\leqslant$ N $\leqslant$ 500000）。第二行含有N个用空格隔开的整数，表示序列中的N个元素。每个元素的值不超过1 000 000 000。N=0是输入数据结束的标志。

输出

每个案例仅输出一行，其中只有一个表示给定序列的逆序数整数。

输入样例

输出样例

0
1

这是本书要讨论，研究的一个典型的计算问题。理解问题是解决问题的最基本的要求，理解计算问题要抓住三个要素：输入、输出和两者的逻辑关系。这三个要素中，输入、输出数据虽然是问题本身明确给定的，如果输入包含若干个案例则要理清每个案例的数据构成。

例如，问题0-1的输入文件inputdata（本书所有计算问题的输入假设均存于文件中，统一记为inputdata）中含有若干个测试案例，每个案例有两行输入数据。第1行中的一个整数N表示案例中给定序列的元素个数。第二行含有表示序列中N个元素的N个整数。当读取到的N=0时意味着输入结束。

所谓输入、输出数据之间的逻辑关系，实质上指的是一个测试案例的输入、输出数据之间的对应关系。为把握这一关系，往往需要认真、仔细地阅读题面，在欣赏题面阐述的故事背景之余，应琢磨、玩味其中所交代的反应事物特征属性的数据意义，以及由事物变化、发展所引发的数据变化规律，由此理顺各数据间的关系，这是设计解决问题的算法的关键所在。

例如，如果我们把问题0-1的一个案例的输入数据组织成一个数组A[1..N]，我们就要计算出序列中使得i<j，A[i]>A[j]成立的所有二元组<i, j>，统计出这些二元组的数目，作为该案例的输出数据加以输出——作为一行写入输出文件outputdata（本书所有计算问题的输出假设均存于文件中，统一记为outputdata）。

对问题有了正确的理解之后，就需要根据数据间的逻辑关系，找出如何将输入数据对应为正确的输出数据的转换过程。这个过程就是通常所称的“算法”。通俗地说，算法就是计算问题的解决之道。

例如，对问题0-1的一个案例数据A[1..N]，为计算出它的逆序数，我们设置一个计数器变量count（初始化为0）。从j=N，A[j]开始，依次计算各元素与其前面的元素（A[1..j−1]）构成的逆序个数，累加到count中。当j<2时，结束计算返回count即为所求。

0.3　算法的伪代码描述

上一节最后一段使用自然语言（汉语）描述了解决“计算逆序数”问题的算法。即如何将输入数据转换为输出数据的过程。在需要解决的问题很简单的情况下（例如“计算逆序数”问题），用自然语言描述解决这个问题的算法是不错的选择。但是，自然语言有一个重要特色——语义二岐性。语义二岐性在文学艺术方面有着非凡的作用：正话反说、双关语……。由此引起的误会、感情冲突……带给我们多少故事、小说、戏剧……。但是，在算法描述方面，语义二岐性却是我们必须避免的。因为，如果对数据的某一处理操作的表述上有二岐性，会使不同的读者做出不同的操作。对同一输入，两个貌似相同的算法的运行，将可能得出不同的结果。这样的情况对问题的解决可能是灾难性的。所以，自然语言不是最好的描述算法的工具。

在计算机上，算法过程是由一系列有序的基本操作描述的。不同的计算机系统，同样的操作，指令的表达形式不必相同。本书并不针对特殊的计算机平台描述解决计算问题的算法，我们需要一个通用的、简洁的形式描述算法，并且能方便地转换成各种计算机系统上特殊表达形式（计算机程序设计语言）所描述的程序。描述算法的通用工具之一叫伪代码。例如，解决上述问题数据输入/输出的伪代码过程可描述如下。

1 打开输入文件inputdata
2 创建输出文件outputdata
3 从inputdata中读取案例数据N
4 while N>0
5   do 创建数组A[1..N]
6      for i←1 to N
7         do 从inputdata中读取A[i]
8      result←GET-THE-INVERSION(A)
9      将result作为一行写入outputdata
10     从inputdata中读取案例数据N
11 关闭inputdata
12 关闭outputdata

其中，第8行调用计算序列A[1..N]的逆序数过程GET-THE-INVERSION(A)是解决一个案例的关键，其伪代码过程如下。

GET-THE-INVERSION(A)               ▷A[1..N]表示一个序列
1 N←length[A]
2 count←0
3 for j←N downto 2
4   do for i←1 to j-1 
5        do if A[i]>A[j]           ▷检测到一个逆序
6              then count←count+1  ▷累加到计数器
7 return count

算法0-1　解决“计算逆序数”问题的一个案例的算法伪代码过程

伪代码是一种有着类似于程序设计语言的严格外部语法（用if-then-else表示分支结构，用for-do、while-do或repeat-until表示循环结构），且有着内部宽松的数学语言表述方式的代码表示方法。它既没有二歧性的缺陷（严格的外部语法），又能用高度抽象的数学语言简练地描述操作细节。

本书所使用的伪代码书写规则如下。

① 用分层缩进来指示块结构。例如，从第3行开始的for循环的循环体由第4～6行的3行组成，分层缩进风格也应用于if-then-else语句，如第5～6行的if-then语句。

② 对for循环，循环计数器在退出循环后仍然保留。因此，一个for循环刚结束时，循环计数器的值首次超过for循环上界。例如在算法0-1中，当第3～6行的for循环结束时，j = N+1；而第4～6行的for循环结束时，i=1−1=0。

③ 符号“ ▷”表示本行的注释部分。例如，算法0-1的开头对参数A的意义进行了解释，第5行说明检测到一个逆序（i<j，A[i]>A[j]），而第6行说明将此逆序累加到逆序数count（count自增1）。

④ 多重赋值形式i ← j← e对变量i和j同赋予表达式e的值；它应当被理解为在赋值操作j ← e之后紧接着赋值操作i ← j。

⑤ 变量（如i，j，及count）都局部于给定的过程。除非特别需求，我们将避免使用全局变量。

⑥ 数组元素是通过数组名后跟括在方括号内的下标来访问。例如，A[i]表示数组A的第i个元素。记号“…”用来表示数组中取值的范围。因此，A[1…i]表示数组A的取值由A[1]到A[i]，i个元素构成的子序列。

⑦ 组合数据通常组织在对象中，其中组合了若干个属性。用域名[对象名]的形式来访问一个具体的域。例如，我们把一个数组A当成一个对象，它具有说明其所包含的元素个数的属性length。为访问数组A的元素个数，我们写length[A]。

表示数组或对象的变量被当成一个指向表示数组或对象的指针。对一个对象x的所有域f，设y ← x将导致f[y] = f[x]。此外，若设f[x]← 3，则不仅有f[x] = 3，且有f[y] = 3。换句话说，赋值y ← x后，x和y指向同一个对象。

有时，一个指针不指向任何对象，此时，我们给它一个特殊的值NIL。

⑧ 过程的参数是按值传递的：被调用的过程以复制的方式接收参数，若对参数赋值，则主调过程不能看到这一变化。

⑨ 布尔运算符“and”和“or”都是短回路的。也就是说，当我们计算表达式“x and y”时，先计算x。若x为FALSE，则整个表达式不可能为TRUE，所以我们不再计算y。另一方面，若x为TRUE，我们必须计算y以确定整个表达式的值。相仿地，在表达式“x or y”中，我们计算表达式y当且仅当x为FALSE。短回路操作符使得我们能够写出诸如“x ≠ NIL and f [x] = y”这样的布尔表达式而不必担心当x为NIL时去计算f [x]。

0.4　算法的正确性

解决一个计算问题的算法是正确的，指的是对问题中任意合法的输入均应得到对应的正确输出。大多数情况下，问题的合法输入无法穷尽，当然就无法穷尽输出是否正确的验证。即使合法输入是有限的，穷尽所有输出正确的验证，在实践中也许是得不偿失的。但是，无论如何，我们需要保证设计出来的算法的正确性。否则，算法设计就是去了它的应用意义。因此，对设计出来的算法在提交应用之前，应当说明它的正确性。这就需要借助我们对问题的认识与理解，利用数学、科学及逻辑推理来证实算法是正确的。例如，对于解决“计算逆序数”问题的算法0-1，其正确性可以表述为如下命题：

当第3～7行的for循环结束时，count已记录下了序列A[1..N]中的逆序数。

如果我们能说明上述命题是真的，那就说明了算法0-1是正确的。由于数组A[1..N]的长度N是任意正整数，所以这是一个与正整数相关的命题。数学中要证明一个与正整数相关的命题有一个有力的工具——数学归纳法。下面我们对本命题中的N进行归纳。

当N=1时第3～7行的for循环重复0次。count保持初始值0，这与A[1..N]=A[1]没有任何逆序相符，结论显然为真。

设N>1且可用算法计算出A[1..N−1]的逆序数count。在此假设下，我们来证明对A[1..N]利用算法0-1也能得到正确的逆序数count。

考虑算法中第3～7行的for循环在j=N时的第一次重复的操作：第4～6行内嵌的for循环从i=1开始到j−1为止，逐一检测是否A[i]>A[j]。若是，意味着找到一个关于A[N]的逆序，第6行count自增1。当此循环结束时count中累积了关于A[N]的逆序数。由于N>1，故第3～6行的外围for循环必定会继续对A[1..N−1]做同样的操作。根据归纳假设，我们知道第3～6行的for循环接下来的重复操作能将A[1..N−1]中个元素的逆序数累加到count中。所以第3～6行for循环结束时，count已记录下了序列A[1..N]中的逆序数。

这样，我们就从逻辑上证明了算法0-1能正确地解决“计算逆序数”问题的一个案例，即算法0-1是正确的。

应当指出，解决一个计算问题时，算法不必唯一。数据的组织方式、解题思路的不同，会导致不同的算法。

例如，将计数器count设置为全局变量，并初始化为0。解决“计算逆序数”问题一个案例的算法还可以表示为如下的形式。

GET-THE-INVERSION(A, N)            ▷A[1..N]表示一个序列
1 if N<2
2     then return
3 for i←1 to N-1 
4   do if A[i]>A[N]                ▷检测到一个逆序
5     then count←count+1           ▷累加到计数器
6 GET-THE-INVERSION(A, N-1)

算法0-2　解决“计算逆序数”问题一个案例的递归算法伪代码过程

这是一个“递归”算法，它在定义的内部（第6行）进行了一次自我调用。受上述算法0-1正确性命题证明的启发，这个算法的思想是基于先计算出A[1..N-1]中关于A[N]的逆序数count，然后将问题归结为计算A[1..N-1]的逆序数的子问题。用相同的方法解决子问题（递归调用自身，注意表示A的长度的第2个参数变成N-1）把子问题的解与count合并就可得到原问题的解。其实，算法0-2与算法0-1仅仅是表达形式不同，本质上等价的：后者用末尾递归（第6行递归调用自身）隐式地替代算法0-1中第3～6行的外层for循环。所以，算法0-2也是正确的。

0.5　算法分析

解决同一问题的不同算法所消耗的计算机系统的时间（占用处理器的时间）和空间（占用内部存储器空间）资源量可能有所不同。算法运行所需要的资源量称为算法的复杂性。一般来说，解决同一问题的算法，需要的资源量越少，我们认为越优秀。计算算法运行所需资源量的过程称为算法复杂性分析，简称为算法分析。理论上，算法分析既要计算算法的时间复杂性，也要计算它的空间复杂性。然而，算法的运行时间都是消耗在已存储的数据处理上的，从这个意义上说，算法的空间复杂性不会超过时间复杂性。出于这个原因，人们多关注于算法的时间复杂性分析。本书中除非特别说明，所说的算法分析，局限于对算法的时间复杂性分析。

算法的运行时间，就是执行基本操作的次数。所谓基本操作，指的是计算机能直接执行的最简单的不可再分的操作。例如对数据进行的算术运算和逻辑运算，以及将数据存储于内存的某个单元。考虑算法0-1，当序列A的元素个数为N时：

GET-THE-INVERSION(A) 
1 N← length[A]                             耗时1个单位
2 count←0                                  耗时1个单位
3 for j← N downt o 2                       耗时N个单位
4   do for i←1 to j-1                      耗时=N(N+1)/2-1个单位
5        do if A[i]>A[j]                   耗时=N(N+1)/2个单位    
6              then count←count+1          耗时不超过=N(N+1)/2个单位
7 return count                      +） 耗时1个单位 
                                           3N2/2+N/2+2

具体地说，第1、2、7行各消耗1个单位时间，总数为3，第3行做N次j与2的比较耗时N，第4行作为外层循环的循环体中一个操作，每次被执行时做j次i与j−1的比较，所以总耗时为N+(N−1)+…+2=N(N+1)/2-1。相仿地，第5、6行作为内层循环的循环体每次被重复j−1次，但它们也在外层循环的控制之下，所以两者的耗时为2(1+ 2+…+N−1)=N(N−1)。把它们相加得到

N+3+N(N+1)/2-1+N(N-1)

　　　　　　　　　　　　　　=N+2+N2/2+N/2+N2-N

　　　　　　　　　　　　　　=3N2/2+N/2+2

一般而言，算法的时间复杂性与输入的规模（算法0-1中序列A的元素个数）相关。规模越大，需要执行的基本操作就越多，当然运行时间就越长。此外，即使问题输入的规模一定，不同的输入也会导致运行时间的不同。对固定的输入规模，使得运算时间最长的输入所消耗的运行时间称为算法的最坏情形时间。通常，人们以算法的最坏情形时间来衡量算法的时间复杂性，并简称为算法的运行时间。例如，在上述的算法0-1的分析中，第3～6行的嵌套循环的循环体的每次重复，第6行并非必被执行，所以我们说其耗时“不超过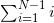 $\sum\nolimits_{i=1}^{N-1}{i}$ =N(N+1)/2个单位”。但我们要考虑的是最坏情形时间，所以运行时间是按N(N+1)/2加以计算的。

对于算法的输入规模为n的运行时间，常记为T(n)。以算法0-1的GET-THE- INVERSION(A)过程为例，数组A[1..N]的元素个数N越大，运行时间T(N)=3N2/2+N/2+2的值就越大。

对算法0-2而言，设其对输入规模为N的运行时间为T(N)。

GET-THE-INVERSION(A, N) 
1 if N<2                              耗时1个单位
2     then return                     耗时不超过1个单位
3 for i←1 to N-1                      耗时N个单位
4     do if A[i]>A[N]                 耗时N-1个单位
5      then count←count+1             耗时不超过N-1个单位
6 GET-THE-INVERSION(A, N-1)      +） 耗时T(N-1) 
                                 T(N)=T(N−1)+3N-1

这是一个在等式两端都含有未知式T的方程，称为递归方程。递归方程可以用迭代法来解，即

T(N)=T(N-1)+3N-1

　　　　　　　　　　　　　　　 =T(N-2)+3(N-1)+3N-2

　　　　　　　　　　　　　　　 =T(N-3)+3(N-2)+3(N-1)+3N-3

　　　　　　　　　　　　　　　 ……

　　　　　　　　　　　　　　　 =T(1)+3*2+…+3(N-1)+3N-(N-1)

　　　　　　　　　　　　　　　 =2+3(1+2+3+…+N)-3-N+1

　　　　　　　　　　　　　　　 =3N(N+1)/2-N

　　　　　　　　　　　　　　　 =3N2/2+N/2

显然，这算法0-1的运行时间大同小异。注意，式中的T(1)指的是算法0-2的第2个参数N=1时的运行时间。显然，这将仅执行其中1～2行的操作，耗时为2个单位。

0.6　算法运行时间的渐近表示

由于计算机技术不断地扩张其应用领域，所要解决的问题输入规模也越来越大，所以对固定的n来计算T(n)的意义并不大，我们更倾向于评估当n→∞时T(n)趋于无穷大的快慢，并以此来分析算法的时间复杂性。我们往往用几个定义在自然数集N上的正值函数Ỹ(n)：幂函数nk（k为正整数），对数幂函数lgkn（k为正整数，底数为2）和指数函数an（a为大于1的常数）作为“标准”，研究极限

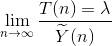　　　　　　　　　　　　　 $\lim_{n\to\infty}\frac{T(n)=\lambda }{\widetilde{Y}(n)}$ 　　　　　　　　　　　　（0-1）

若λ为一正常数，我们称Ỹ(n)是T(n)的渐近表达式，或称T(n)渐近等于Ỹ(n)，记为T(n)=Θ(Ỹ(n))，这个记号称为算法运行时间的渐近Θ-记号，简称为Θ-记号。例如，算法0-1的运行时间为T(n)=2n2+4n+3，取Ỹ(n)=n2，由于

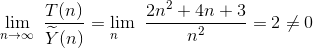
$\lim {}_{n\to \infty }^{{}}\ \frac{T(n)}{\widetilde{Y}(n)}=\lim_{n\quad}^{{}}\ \frac{2{{n}^{2}}+4n+3}{{{n}^{2}}}=2\ne 0$

所以，我们有T(n)=Θ(n2)，即此T(n)渐近等于n2。其实，在一个算法的运行时间T(n)中省略最高次项以外的所有项，且忽略最高次项的常数系数，就可得到它的渐近表达式。例如，用此方法也能得到算法0-1的运行时间T(N)=3N2/2+N/2+2=Θ(N2)，算法0-2的运行时间T(N)= 3N2/2+N/2=Θ(N2)。在这个意义上，我们可以再次断言——算法0-1和算法0-2是等价的。

如果两个算法的运行时间的渐近表达式相同，则将它们视为具有相同的时间复杂度的算法。显然，渐近时间为对数幂的算法优于渐近时间为幂函数的算法，而渐近时间为幂函数的算法则优于渐近时间为指数函数的算法。我们把渐近时间为幂函数的算法称为具有多项式时间的算法。渐近时间不超过多项式的算法我们称其为有效的算法。通常认为运行时间为指数式的算法不是有效的。

渐近记号除了Θ外，还有两个常用的记号O和Ω。它们的粗略意义如下：

考察定义域为自然数集N的正值函数Ỹ(n)和T(n)构成的极限式0-1的值λ，若λ $\leqslant$ 1为一常数，则称函数T(n)渐近不超过函数Ỹ(n)，记为T(n) = O (Ỹ(n))；若λ>1为常数或为+∞，则称函数T(n)渐近不小于函数Ỹ(n)，记为T(n)= Ω(Ỹ(n))。例如lgkn=O(nk)，反之，lgkn=Ω(nk)。显然，T(n)=Θ(Ỹ(n))当且仅当T(n) = O (Ỹ(n))且T(n)= Ω(Ỹ(n))。对算法运行时间的深入讨论读者可参考配书的短视频“算法的运行时间”。

下面我们用以上讨论过的概念、术语、记号和方法再讨论一个计算问题。

问题0-2　移动电话

问题描述

假定在坦佩雷〔芬兰城市〕地区的第四代移动电话基站如下述方式运行。该地区划分成很多四方块，这些四方形的小区域形成了S×S矩阵。该矩阵的行、列均从0开始编码至S-1。每个方块区域包含一个基站。方块内活动的手机数量是会发生变化的，因为手机用户可能从一个方块区域进入到另一个方块区域，也有手机用户开机或关机。每个基站会报告所在区域内手机活动数的变化。

写一个程序，接收这些基站发来的报告，并应答关于指定矩形区域内的活动手机数的查询。

输入

输入从标准输入设备中读取表示查询的整数并向标准输出设备写入整数以应答查询。输入数据的格式如下。每一行输入数据包含一个表示指令编号的整数及一些表示该指令的参数。指令编号及对应参数的意义如下表所示。

指令编号	参数	意义
0	S	创建一个的S×S矩阵并初始化为0。该指令仅发送一次，且总是为第一条指令
1	X Y A	区域（X, Y）增加A个活动手机
2	L B R T	查询所有方块区域（X, Y）内活动手机数量之和。其中，L $\leqslant$ X $\leqslant$ R, B $\leqslant$ Y $\leqslant$ T
3		终止程序。该指令也仅发送一次，且必为最后一条指令

假定输入中的各整数值总是在合法范围内，无需对它们进行检验。具体说，例如A是一个负数，它不可能将某一方块区域中的手机数减小到0以下。下标都是从0开始的，即若矩阵规模为4×4，必有0 $\leqslant$ X $\leqslant$ 3且0 $\leqslant$ Y $\leqslant$ 3。

我们假定：

矩阵规模：1×1 $\leqslant$ S×S $\leqslant$ 1024×1024。

任何时候方块区域内的活动手机数：0 $\leqslant$ V $\leqslant$ 32767。

修改值：−32768 $\leqslant$ A $\leqslant$ 32767。

不存在指令号：3 $\leqslant$ U $\leqslant$ 60002。

整个区域内的最大活动手机数：M= 230。

输出

你的程序对除了编号为2以外的指令无需做任何应答。若指令编号为2，程序须向标准输出设备写入一行应答的答案。

输入样例

输出样例

3
4

解题思路

（1）数据的输入与输出

根据输入文件的格式，测试案例由若干条指令组成，每条指令占1行。依次读取各条指令存放于数组cmds中。指令3为结束标志。对指令序列cmds逐一执行，对指令2保存执行结果于数组result中。所有指令执行完毕后，将result中的数据逐行输出到输出文件。

1 打开输入文件inputdata
2 创建输出文件outputdata
3 创建指令序列cmds←Ø
4 从inputdata中读取案例数据cmd
5 while cmd≠3
6    do if cmd=0
7          then 从inputdata中读取S
8               INSERT(cmds, (cmd, S))
9          else if cmd=1
10              then 从inputdata中读取X, Y, A
11                   INSERT(cmds, (cmd, X, Y, A))
12              else 从inputdata中读取L, B, R, T
13                   INSERT(cmds, (cmd, L, B, R, T))
14       从inputdata中读取cmd
15 result←MOBIL-PHONE(cmds)
16 for each rresult
17   do 将r作为一行写入outputdata
18 关闭inputdata
19 关闭outputdata

其中，第15行调用计算指令序列cmds显示结果的过程MOBIL-PHONE(cmds)是解决一个案例的关键。

（2）解决一个案例的算法过程

首先创建数组result用来存储查询指令（指令2）的执行结果。cmds[1]是指令0，它的参数s决定了坦佩雷地区移动通信网的规模。用S创建一个二维数组tampere[0..S-1, 0..S-1]，并将所有元素初始化为0。从i=2开始逐一执行指令cmds[i]。若cmds[i]是指令1，则用其参数x, y, a在tampere[x][y]累加a。若cmds[i]是指令2，则在其参数l，b，r，t指定的（l, b）为左下角，（r, t）为右上角的范围内计算移动电话的数量，将计算结果加入数组result中。所有指令执行完毕后，返回result。

MOBIL-PHONE(cmds)
1 n←length[cmds]
2 析取指令cmds[1]的参数S
3 创建二维数组tampere[0..S-1, 0..S-1]并将元素初始化为0
4 创建数组result←Ø
5 for k←2 to n
6     do 从cmds[k]中析取cmd
7     if cmd=1
8          then 从cmds[k]中析取参数X, Y, A
9              tampere[X][Y] ← tampere[X][Y]+A
10             if tampere[X][Y]<0
11               then tampere[X][Y]=0
12         else从cmds[k]中析取参数L, B, R, T
13             count←0
14             for i←L to R
15               do for j←B to T
16                 do count←count+tampere[i][j]
17          INSERT(result, count)
18 return result

算法0-3　解决“移动电话”问题的算法过程

这个算法的代码结构类似于算法0-1，算法的结构主体是嵌套在一起的若干个循环。由于我们用渐近表达式表示算法的运行时间，所以对这种结构的算法，在算法分析时循环之外常数时间完成的操作可以不予考虑。例如，本算法中第1～4行及第18行的操作，分析时可忽略。我们把目光聚焦于第5～17行的for循环。这个循环共重复Θ(n)（准确地说是n−1，但作为渐近式与n等价）次。循环体中是一个分支结构，分支之一是处理指令1的第8～11行操作，耗时为常数Θ(1)（准确地说是4，渐进等价于1）。另一分支是处理指令2的第12～17行，该分支中，除了第12、13、17行的常数时间操作外（第17行是在数组result的尾部添加新的元素，耗时亦为Θ(1)），第14～16行是一个两重嵌套for循环。这两重循环分别重复r-l和t-b次。循环体内的操作耗时Θ(1)（1次赋值操作）。所以这两重循环的耗时为Θ((R-L)(T-B))。这个结果看起来似乎很精致，但实际上我们并不知道L，B，R，T的具体值，但我们知道0 $\leqslant$ L，B，R，T $\leqslant$ S。也就是说必有0 $\leqslant$ R-L, T-B $\leqslant$ S。因此，用渐近表达式我们可以将这个嵌套循环的耗时记为O(S2)（意味着耗时不差过S2）。再由于它内嵌于第5～17行的最外层for循环之内，若n条指令中指令2数目m占有一定比例（即存在常数c使得n=cm）则第12～17行的操作耗时可表为O(nS2)。于是，我们得出算法0-3的运行时间为O(nS2)。

0.7　算法的程序实现

有了解决问题的正确算法，就可以利用一种计算机程序设计语言将算法实现为可在计算机上运行的程序。本书选用业界使用最广泛、最成熟的C++语言来实现解决每一个问题的算法。C++语言是面向对象的程序设计语言，它为程序员提供了一个庞大的标准库。有趣的是，C++脱胎于C语言。所以，读者若具有C语言某种程度的训练，对于理解本书提供的C++代码一定是大有裨益的。闲话少说，让我们先来一睹C++语言程序的“芳容”吧。

解决问题0-1“计算逆序数”的C++程序如下。

1 #include <fstream>
2 #include <iostream>
3 #include <vector>
4 using namespace std;
5 int getTheInversion(vector<int> A){
6   int N=int(A.size());
7   int count=0;
8   for (int j=N-1; j>0; j--)
9       for (int i=0; i<j; i++)
10        if(A[i]>A[j])
11          count++;
12   return count;
13 }
14 int main(){
15     ifstream inputdata("Get The Inversion/inputdata.txt");//输入文件流对象
16     ofstream outputdata("Get The Inversion/outputdata.txt");//输出文件流对象
17     int N=0;
18     inputdata>>N;
19     while (N>0) {
20         vector<int> A(N);
21         for (int i=0; i<N; i++)
22                inputdata>>A[i];
23         int result=getTheInversion(A);
24         cout<<result<<endl;
25         outputdata<<result<<endl;
26         inputdata>>N;
27    }
28    inputdata.close();
29    outputdata.close();
30    return 0;
31 }

程序0-1　实现解决“计算逆序数”问题算法的C++程序

关于C++语言的各种细节（语言基础、支持语言的库、运用语言的各种技术等），我们将在本书的第9章，通过实现本书中算法的实际代码展开讨论。此处，我们仅仅借程序0-1做一个初步的认识。

我们可以把程序分成三部分观察。第一部分就是程序中的第1～4行，执行预编译指令。第二部分是第5～13行的函数getTheInversion定义。第三部分是第14～31行，程序的主函数。下面我们就这三个部分逐一加以简单说明。

① #include指令用来为程序引入“库”——包含各种已定义的数据类型、类、函数等，实现优质代码的重用，以提高程序设计的工作效率和程序的质量——搭建一座方便之桥。由于C++中任何运算成分（类型、变量、常量、函数……）均需先声明、后使用，所以头文件中就声明了一组程序所需的具有特殊意义的运算成分。用include指令将指定的头文件加载进来，程序员就可以方便地访问这些成分了。此处，首行指令#include <fstream>意味着本程序可以使用系统提供的文件输入输出流类的对象，方便地输入、输出数据。本书中所有算法的实现代码涉及输入输出的操作都需要进行文件的读写操作，所以这条指令将出现在每一个程序文件的首要位置。后面的两条分别引入控制台输入输出对象（cin、cout）和向量类（vector，这是C++标准模板库STL提供的可变长数组类模板）。这些类、对象的引入给大家带来了极大的方便。语句using namespace std（语句以分号结尾）指出，以上引入的类或对象都是标准库中的，可按名称直接访问。

② 细心的读者可能已经发现，第5～13行定义的函数int getTheInversion(vector<int> A)就是对算法0-1中伪代码过程GET-THE-INVERSION(A)的实现。除了某些细节，程序代码与伪代码几乎是一样的。如果你也有这样的感觉，我们就有了一种默契：只要有了伪代码，我们就能很快地写出它的实现程序——算法伪代码就是程序开发的“施工蓝图”。

③ 第14～31行定义的main函数也就是我们在算法0-1之前描述的“计算逆序数”问题数据的输入与输出的伪代码的实现。如果了解到“>>”和“<<”是C++数据流（文本文件就是一个数据流）的输出、输入操作符，则会感觉到这段代码几乎就是伪代码的翻版。

程序0-1存储为文件夹Get The Inversion的文件Get The Inversion.cpp。读者要在计算机上运行这个程序，需要在你的计算机上安装一个C++开发软件（譬如，在PC上安装一个Visual C++软件，在iMac上安装一个Xcode），然后创建一个项目，在其中加载文件laboratory/Get The Inversion/Get The Inversion.cpp。

同样，解决问题0-2“移动电话”的C++程序是存于文件夹laboratory/Mobil Phone中的文件Mobil Phone.cpp。

0.8　从这里开始

作为本书讨论的起点，本章通过解决一个典型的计算问题“计算逆序数”，明确了诸如算法、伪代码、算法分析、C++程序等概念、术语或名称。通过讨论问题“移动电话”给出了本书每个问题讨论的体例：描述问题——理解问题——设计算法——分析算法的效率。

如果你是一位编程初学者，在看了这两个例子后是否会有这样的问题：怎么会想到这样解这些问题？其实，这和你在学校里学习数学时解应用题很相像。首先，看看题目是归类于代数、几何还是微积分？如果是代数题，再看是用解方程方法还是用计算的方法？本书以后的六章将常见的计算问题分成计数问题、集合与查找问题、简单模拟问题、组合问题、组合优化问题和图的搜索问题，针对每一类问题深入讨论了各种问题的思路、方法和技术。所有这些，都是通过一个个有趣的计算问题的解答而展开的。本书的第8章还为喜欢独立思考的读者提供了几个待解的计算问题，读者可试着用前几章讨论过的方法解决这些问题，说不定会给你带来别样的快乐体验。第9章就本书所解决的诸多问题的程序代码，与读者分享了用C++编程的乐趣。相信读者掩卷之时，必会对算法设计、程序运行等现代人应具有的计算思想有所认识，对解决这类问题的思路有所启发，这恰是笔者写这本书的愿望。

准备好了，我们就从这里开始吧。

人民邮电出版社有限公司

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
打赏
0
评论
《趣题学算法》Chapter 0 从这里开始

Chapter 0　从这里开始 0.1　App程序与算法 0.2　计算问题 0.3　算法的伪代码描述 0.4　算法的正确性 0.5　算法分析 0.6　算法运行时间的渐近表示 0.7　算法的程序实现 0.8　从这里开始 0.1　App程序与算法信息时代，人们时刻都在利用各种App解决生活、工作中的问题，或获取各种服务。早晨，手机里设定的闹钟铃声（或你喜欢...
复制链接

扫一扫