从硕士的时候,偶尔在论文中,看到拓扑空间这个名词,但没有真正理解它是什么意思,现在抽出时间总结一下。
拓扑空间有时候也直接称为拓扑,一个集合 X X X 的拓扑 τ \tau τ 表示针对该集合内元素的一些组合满足下列条件:
- 空集与 X X X 本身属于 τ \tau τ
- τ \tau τ 中任意元素的交集属于 τ \tau τ
- τ \tau τ 中任意元素的并集属于 τ \tau τ
因此,拓扑可以理解为一个给定集合内元素所组成的,另外一个满足上面三个条件的集合。
下面,用维基百科的一个图形例子来说明。
给定的集合 X = { 1 , 2 , 3 } X=\{1,2,3\} X={1,2,3},下面的六个新集合中,最后两个并不属于 X X X 的拓扑。
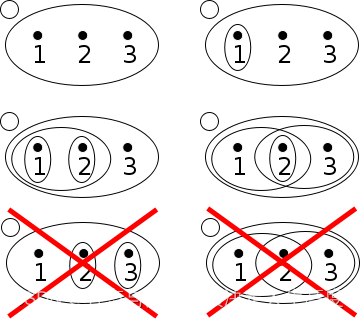
- 左上的集合为 {{1, 2, 3}},满足三个条件
- 右上的集合为 {1,{1,2,3}},满足三个条件
- 中左的集合为 {{1},{2},{1,2},{1,2,3}},满足三个条件
- 中右的集合为 {{1,2},{2,3},{2},{1,2,3}},满足三个条件
- 左下的集合为 {{2},{3},{1,2,3}} 不满足 {2} 与 {3} 的并集属于该拓扑集合
- 右下的集合为 {{1,2},{2,3},{1,2,3}} 不满足 {1,2} 与 {2,3} 的交集属于该拓扑集合
注:向量空间也是拓扑空间,但是拓扑空间不一定是向量空间。因为向量空间的定义要更严格些,要满足那八个公理(关于向量加法与乘法的结合律分配律等)。








 拓扑空间是数学中的一个重要概念,它由集合X及其满足特定条件的子集集合τ构成。这些条件包括空集和X自身属于τ,τ中元素的交集及并集仍属于τ。博客通过一个例子展示了哪些集合组合构成了拓扑,并指出向量空间是拓扑空间的特例,但反之不成立。
拓扑空间是数学中的一个重要概念,它由集合X及其满足特定条件的子集集合τ构成。这些条件包括空集和X自身属于τ,τ中元素的交集及并集仍属于τ。博客通过一个例子展示了哪些集合组合构成了拓扑,并指出向量空间是拓扑空间的特例,但反之不成立。


















 1256
1256

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










