幂函数与指数函数的近似

幂函数 $(1+x{)}^{\alpha }$ 可以近似为指数函数 $e^{\alpha x}$，甚至可以进一步近似为 $1+\alpha x$。在一本书中指数平滑方法的介绍中见到了这个近似，总结一下。

1. $(1+x{)}^{\alpha }\approx 1+\alpha x$

对 $(1+x{)}^{\alpha }$ 在 $x=0$ 处泰勒展开，可以得到
$$(1+x{)}^{\alpha }=1+\alpha x+\frac{\alpha (\alpha -1)}{2}{x}^2+\frac{\alpha (\alpha -1)(\alpha -2)}{6}{x}^3+\dots$$

当 $|x|<1$ 时，$x^2,x^3,\dots$ 越来越小，若进一步 $|\alpha x|\ll 1$ (表示 $|\alpha x|$ 足够小于 1)，则上式中右端各项会越来越小，可以将后面的项省略，所以 $(1+x{)}^{\alpha }\approx 1+\alpha x$

• 没有找到上面这两个条件的严谨证明，但似乎也是合理的

2. $(1+x{)}^{\alpha }\approx e^{\alpha x}$

这个近似可以通过泰勒展开，轻易看出：
$$e{}^{\alpha }x=1+\alpha x+\frac{{\alpha }^2}{2}{x}^2+\frac{{\alpha }^3}{6}{x}^3+\dots$$

当 $|x|$ 比较小时，$(1+x{)}^{\alpha }$ 与 $e^{\alpha x}$ 就比较接近。

• 指数平滑方法中，第 $i$ 个历史需求值权重 $\alpha (1-\alpha {)}^i$ 可以近似为 $\alpha e^{-\alpha i}$，下面这些图形中显示两个函数的近似程度

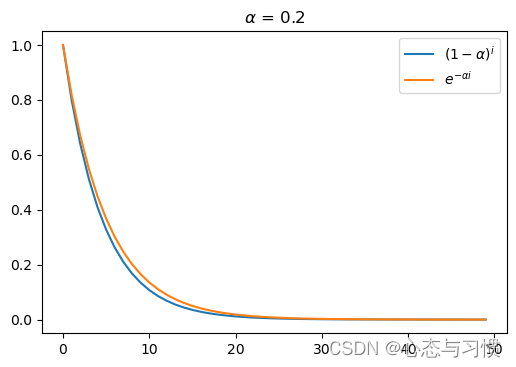
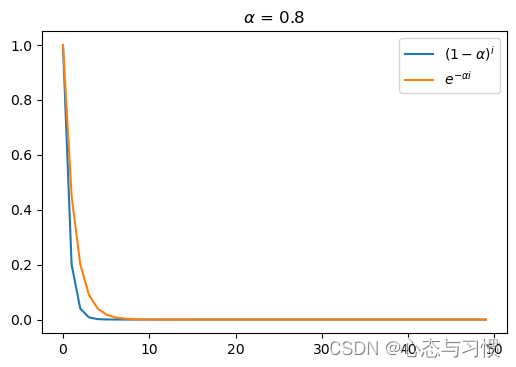
• 从图形上，确实比较接近的，尤其是当 $\alpha$ 比较小时。

代码：

import numpy as np
import matplotlib.pyplot as plt


alpha = 0.2
x = np.arange(0, 50)
y1 = [(1 - alpha)**i for i in x]
y2 = [np.exp(-alpha*i) for i in x]

plt.plot(x, y1, label = r'$(1-\alpha)^i$')
plt.plot(x, y2, label = r'$e^{-\alpha i}$')
plt.title(r'$\alpha$ = ' + str(alpha) )
plt.legend()
plt.show()

plt.figure()
alpha = 0.5
x = np.arange(0, 50)
y1 = [(1 - alpha)**i for i in x]
y2 = [np.exp(-alpha*i) for i in x]

plt.plot(x, y1, label = r'$(1-\alpha)^i$')
plt.plot(x, y2, label = r'$e^{-\alpha i}$')
plt.title(r'$\alpha$ = ' + str(alpha) )
plt.legend()
plt.show()

plt.figure()
alpha = 0.8
x = np.arange(0, 50)
y1 = [(1 - alpha)**i for i in x]
y2 = [np.exp(-alpha*i) for i in x]

plt.plot(x, y1, label = r'$(1-\alpha)^i$')
plt.plot(x, y2, label = r'$e^{-\alpha i}$')
plt.title(r'$\alpha$ = ' + str(alpha) )
plt.legend()
plt.show()