12.5 函数的幂级数展开式的应用

 

12.5 函数的幂级数展开式的应用

第十二章 无穷级数

第五节 函数的幂级数展开式的应用

一、近似计算

有了函数的幂级数展开式，就可以用它来进行近似计算，即在展开式有效的区间上，函数值可以近似地利用这个级数按精确度要求计算出来。

例1：计算 240\sqrt{240}240​ 的近似值，要求误差不超过 0.0001

解答：

因为

取 m=12m = \frac{1}{2}m=21​，x=−3243=−181x = -\frac{3}{243} = -\frac{1}{81}x=−2433​=−811​

所以在二项展开式（公式 4-12）中，取

即得

这个级数收敛很快。取前两项的和作为 240\sqrt{240}240​ 的近似值，其误差（也叫做截断误差）为

于是取近似式为

为了使“四舍五入”引起的误差（叫做舍入误差）与截断误差之和不超过 10−410^{-4}10−4，计算时应取五位小数，然后再四舍五入。因此最后得

学习收获：

通过这个例题，我们学会了如何利用幂级数展开进行近似计算，并理解了截断误差和舍入误差的概念。

解答：

取这级数前 nnn 项的和作为 ln⁡2\ln 2ln2 的近似值，其误差为 ∣Rn∣≤1n+1|R_n| \leq \frac{1}{n+1}∣Rn​∣≤n+11​

为了保证误差不超过 10−410^{-4}10−4，就需要取级数的前 10000 项进行计算。这样做计算量太大了，我们必须用收敛较快的级数来代替它。

把公式（4-10）

中将 xxx 换成 −x-x−x，得

两式相减，得到不含有偶次幂的展开式

令 x=13x = \frac{1}{3}x=31​，得

取前四项作为 ln⁡2\ln 2ln2 的近似值，其误差为

于是取

考虑到舍入误差，计算时应取五位小数：

因此得

学习收获：

通过这个例题，我们学习了如何通过转换变量和重新组合幂级数来找到更快收敛的级数，进而实现更高效的近似计算。

例3：利用幂级数求 sin⁡9∘\sin 9^\circsin9∘ 的近似值，并估计误差

解答：

首先把角度化成弧度，

从而

其次估计这个近似值的精确度。在 sin⁡x\sin xsinx 的幂级数展开式（公式 4-8）中令 x=π20x = \frac{\pi}{20}x=20π​，得

等式右端是一个收敛的交错级数，且各项的绝对值单调减少。取它的前两项之和作为 sin⁡π20\sin \frac{\pi}{20}sin20π​ 的近似值，其误差为

因此取

这时误差不超过 10−510^{-5}10−5。

学习收获：

通过这个例题，我们学会了如何利用幂级数展开进行近似计算，并估计误差的大小，保证结果的精度。

解答：

将 ex2e^{x^2}ex2 的幂级数展开式（公式 4-7）中的 xxx 换成 −x2-x^2−x2，就得到被积函数的幂级数展开式

于是，根据幂级数在收敛区间内逐项可积，得

取前四项的和作为近似值，其误差为

算得

学习收获：

通过这个例题，我们学习了如何利用幂级数展开来计算定积分，并理解了通过逐项积分来求解积分的近似值。

解答：

由于

因此所给积分不是反常积分，若定义被积函数在 x=0x = 0x=0 处的值为 1，则它在积分区间 [0,1][0,1][0,1] 上连续。

展开被积函数，有

在区间 [0,1][0,1][0,1] 上逐项积分，得

取前三项的和作为积分的近似值：

学习收获：

通过这个例题，我们学习了如何利用幂级数展开计算反常积分的近似值，并理解了逐项积分的技巧。

总结

通过这些例题的详细解析，我们不仅掌握了函数幂级数展开式在近似计算中的应用，还学到了如何估计计算误差，保证结果的精度。这些数学思想和技巧在实际问题的解决中有着广泛的应用，希望大家能通过这些例题的分析更好地理解和掌握幂级数展开的应用。

 

 

二、微分方程的幂级数解法

这里，我们简单介绍一阶微分方程和二阶齐次线性微分方程的幂级数解法。

一阶微分方程

为求一阶微分方程 满足初值条件 y(x0)=y0y(x_0) = y_0y(x0​)=y0​ 的特解，如果其中函数 f(x,y)f(x, y)f(x,y) 是 (x−x0)(x - x_0)(x−x0​)、(y−y0)(y - y_0)(y−y0​) 的多项式那么可以设所求特解可展开为 x−x0x - x_0x−x0​ 的幂级数：

其中 a1,a2,…,an,…a_1, a_2, \ldots, a_n, \ldotsa1​,a2​,…,an​,… 是待定的系数。把（公式 5-2）代入（公式 5-1）中，便得一恒等式，比较所得恒等式两端 x−x0x - x_0x−x0​ 的同次幂的系数，就可定出常数 a1,a2,…a_1, a_2, \ldotsa1​,a2​,…，以这些常数为系数的级数（公式 5-2）在其收敛区间内就是方程（公式 5-1）满足初值条件 y(x0)=y0y(x_0) = y_0y(x0​)=y0​ 的特解。

例6 求方程 dydx=−y−x\frac{dy}{dx} = -y - xdxdy​=−y−x 满足 y(0)=2y(0) = 2y(0)=2 的特解。

解答：

这时，x0=0,y0=2x_0 = 0, y_0 = 2x0​=0,y0​=2。故设方程的特解为

由此，得

将 yyy 及其导数的幂级数展开式代入方程，得

上式为恒等式，比较上式两端 xxx 的同次幂的系数，得：

由数学归纳法可得：

于是，得

这就是所求的特解。

二阶齐次线性微分方程

关于二阶齐次线性方程

用幂级数求解的问题，我们先叙述一个定理：

定理： 如果方程（公式 5-3）中的系数 P(x)P(x)P(x) 与 Q(x)Q(x)Q(x) 可在 −R<x<R-R < x < R−R<x<R 内展开为 xxx 的幂级数，那么在 −R<x<R-R < x < R−R<x<R 内方程（公式 5-3）必有形如 的解。

这定理的证明从略。

解答：

这里 P(x)=0P(x) = 0P(x)=0，Q(x)=−xQ(x) = -xQ(x)=−x 在整个数轴上满足定理的条件。因此所求的解可在整个数轴上展开成 xxx 的幂级数

由条件 y(0)=0y(0) = 0y(0)=0，得 a0=0a_0 = 0a0​=0。对级数（公式 5-4）逐项求导，有

由条件 y′(0)=1y'(0) = 1y′(0)=1，得 a1=1a_1 = 1a1​=1。于是所求特解 yyy 及其导数的展开式成为

对级数（公式 5-6）逐项求导，得

把（公式 5-5）和（公式 5-7）代入所给方程，并按 xxx 的升幂集项，得

因为上式是恒等式，所以上式左端各项的系数必全为零，于是有

一般地，

从这递推公式可以推得：

于是所求的特解为：

这个例子展示了如何通过幂级数展开法求解二阶齐次线性微分方程，并验证了幂级数解法的有效性。

 

 

 

三、欧拉公式

设有复数项级数为

其中 unu_nun​ 与 vnv_nvn​ (n=1,2,3,…n = 1, 2, 3, \ldotsn=1,2,3,…) 为实常数或实函数。如果实部所成的级数

收敛于和 uuu，并且虚部所成的级数

收敛于和 vvv，那么就说级数（公式 5-8）收敛且其和为 u+viu + viu+vi。

如果级数（公式 5-8）各项的模所构成的级数 收敛，那么称级数（公式 5-8）绝对收敛。由于 那么级数（公式 5-9）与（公式 5-10）绝对收敛，从而级数（公式 5-8）收敛。

考察复数项级数

可以证明级数（公式 5-11）在整个复平面上是绝对收敛的。在 xxx 轴上 (z=xz = xz=x) 它表示指数函数 exe^xex。在整个复平面上我们用它来定义复变量指数函数，记作 eze^zez。于是 eze^zez 定义为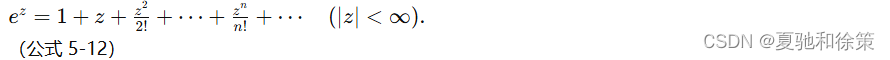

当 x=0x = 0x=0 时，zzz 为纯虚数 yiyiyi，（公式 5-12）式成为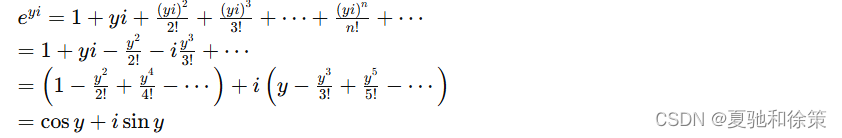

把 yyy 换写为 xxx，上式变为

这就是欧拉（Euler）公式。

应用公式（5-13），复数 zzz 可以表示为指数形式：

其中 r=∣z∣r = |z|r=∣z∣ 是 zzz 的模，θ=arg⁡z\theta = \arg zθ=argz 是 zzz 的辐角（图 12-5）。

在（5-13）式中把 xxx 换成 −x-x−x，又有

把上式与（5-13）相加或相减，得：

这两个式子也叫做欧拉公式。公式（5-13）或（5-15）式揭示了三角函数与复变量指数函数之间的一种联系。

最后，根据定义式（5-12），并利用幂级数的乘法，我们不难验证

特殊地，取 z1z_1z1​ 为实数 xxx，z2z_2z2​ 为纯虚数 yiyiyi，则有

通过这些公式和例子，我们不仅掌握了复数项幂级数的基本性质和绝对收敛性，还理解了复变量指数函数的定义和欧拉公式的应用。这些知识在复分析和工程应用中都有重要意义。