梯度下降法求解感知机模型

梯度下降法求解感知机模型

1. 感知机学习模型

   感知机是一个二分类的线性分类问题，求解是使误分类点到超平面距离总和的损失函数最小化问题，详细内容参见《线性分类模型--感知机》。采用的是随机梯度下降法，首先任意选取一个超平面w0和b0，然后用梯度下降法不断地极小化目标损失函数，极小化过程中不是一次使所有误分类点的梯度下降，而是一次随机选取一个误分类点使其梯度下降。假设误分类点集合M是固定的，那么损失函数L(w,b)的梯度：

                                     

随机选取一个误分类点，对w和b进行更新：

                                        

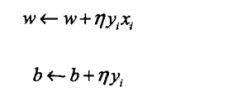
其中n是步长，又称为学习率(learning rate)，这样通过迭代可以使损失函数L(w,b)不断减小，直到训练集中没有误分类点。直观的解释：当一个实例点被误分类，即位于超平面的错误一侧时，则调整w和b的值，使分离超平面向该误分类点的一侧移动，以减少该误分类点与超平面间的距离，直至超平面越过该分类点使其正确分类[1]。注意：当训练数据集线性可分时，这个迭代是收敛的，也就是经过有限次数的迭代是可以找到最优的超平面的[1]。下面就详细讲解这个迭代的过程。

2. 梯度下降法