群体遗传学的数学原理-CSDN博客

本文链接：https://blog.csdn.net/ruby912/article/details/101682198

本文深入探讨了群体遗传学的数学基础，包括一对等位基因的孟德尔群体、基因频率计算、哈温伯格定律、遗传多态性和群体中亲属关系的研究。此外，还涉及了系统树重建的方法，如UPGMA、最大简约法和最大似然法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

群体遗传学数学基础

数学基础
一对等位基因孟德尔群体及其数量表示
遗传多态性
群体中亲属关系研究
系统树重建
其他参考

数学基础

以下全明白才能看懂之后的：

一对等位基因孟德尔群体及其数量表示

孟德尔群体：群体遗传学研究对象，是能够互交繁殖的个体集合
孟德尔群体的遗传结构：它的基因分布和基因型分布

1.群体遗传结构

(AA,Aa,aa)=(p₂,p₁,p₀)
(A,a)=(p,q)

2.基因频率由基因型频率唯一确定

p=p₂+1/2p₁
q=p₀+1/2p₁

3.哈温伯格定律

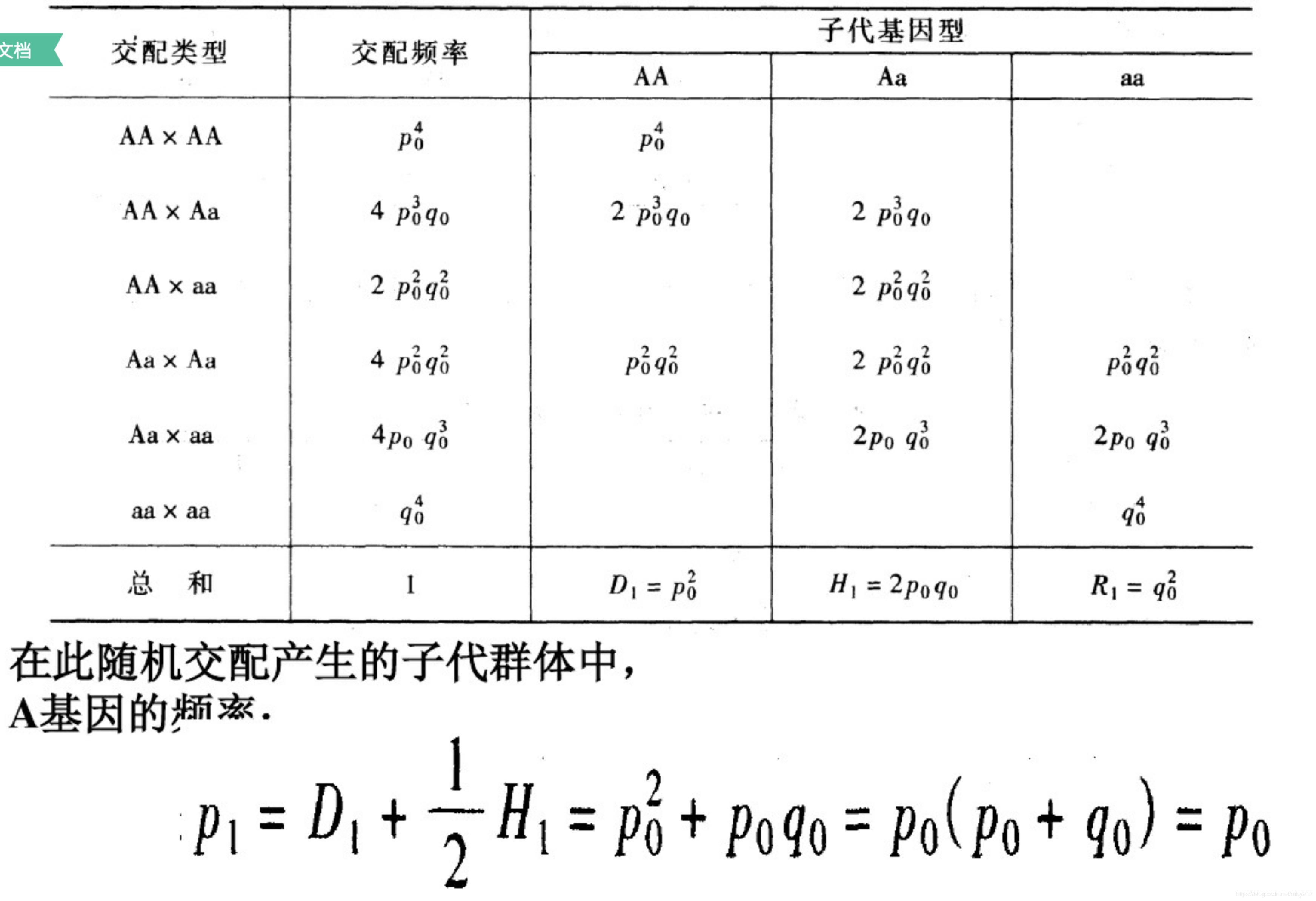
在随机交配的大孟德尔群体中，其遗传结构为
(AA,Aa,aa)=(p²,2pq,q²)
(A,a)=(p,q)
随机交配下的平衡：

4.平衡群体的性质

4.1 Shannon信息熵最大

平衡群体：

(AA,aA,Aa,aa)=(p²,pq,pq,q²)

由基因库行程的基因型（正反交分开）信息源：

G =
[AA Aa aA aa
p₁₁ p₁₂ p₂₁ p₂₂]

由pij计算基因A，a的频率p，q ：
在这里插入图片描述

基因型的信息熵：
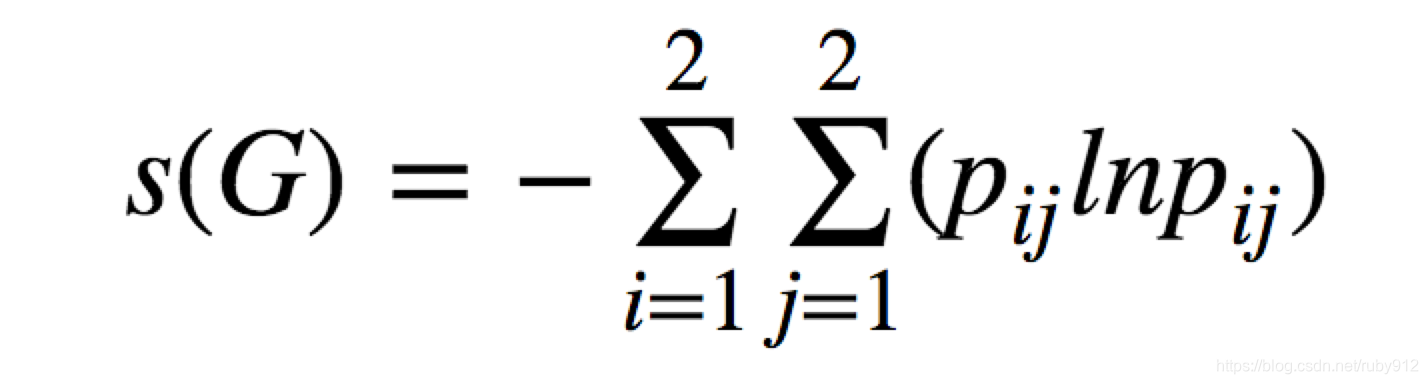使s(G)最大的基因型频率可归结为如下条件极值：

https://www.numberempire.com/latexequationeditor.php
\begin{cases}
\sum\limits_{i=1}^2\sum\limits_{j=1}^2(p_{ij})=1 \\
p=1/2\sum\limits_{j=1}^2(p_{1j}+p_{j1}) \\
q=1/2\sum\limits_{j=1}^2(p_{2j}+p_{j2}) \\
s(G)=-\sum\limits_{i=1}^2\sum\limits_{j=1}^2(p_{ij}lnp_{ij})=max
\end{cases} \

构建拉格朗日函数约束条件求解：