计算几何之多边形

最近解决一个多边形带洞的问题，需要判断多边形的顶点顺序，顺便复习下计算几何的一些基础知识。。
判断顶点顺序需要计算多边形的面积，面积有正负之分，符号决定了顺时针CW还是逆时针CCW。计算面积两种思路：
- 直角梯形的思路
- 向量叉乘

直角梯形思路

任何一个边p0p1，两个顶点向x轴投垂线，构成了直角梯形。它的面积是

(p1.x – p0.x) * (p1.y + p2.y) / 2.0

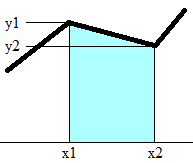
面积符号受deltaX，averageY影响。二者综合影响。

下图中，多边形面积等于所有边与x轴构成直角梯形面积总和。N个顶点，则N个边的面积之和，尤其注意首尾顶点(n-1, 0)的 这个线段的面积需要考虑进去。。

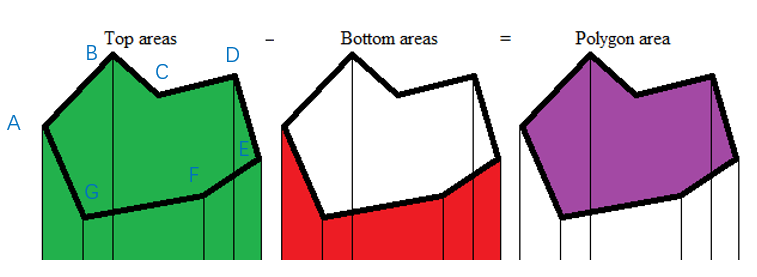
上图中，多边形顶点顺序为顺时针ABCDEFG，
TopAreas是AB，BC，CD，DE 与x轴构成的梯形，面积都大于0；
BottomAreas是EF，FG，GA与x轴构成的梯形，deltax为负，面积都小于0；最终多边形面积为正。

因此

这种方式下，多边形顶点顺序为逆时针，则面积为负值；顺时针时候，面积为正值。

向量叉乘的方式

向量叉乘
最经简单的例子，

unit_x(1, 0, 0) cross unit_y(0, 1, 0) = unit_z(0, 0, 1)

叉乘的右手法则：右手四指，从a开始以不超过180的转角握向b，大拇指的指向就是叉乘结果向量的方向。
2D向量叉乘的物理意义：a向量叉乘b向量的模，代表|b|*sin为高，a为底的三角形面积。面积可以有符号，叉乘向量是z轴正向时，面积为正，否则为负。

多边形的面积计算，多边形每个边两个端点跟原点组成一系列三角形，它们的面积有正负，所面积之和就是多边形的面积。

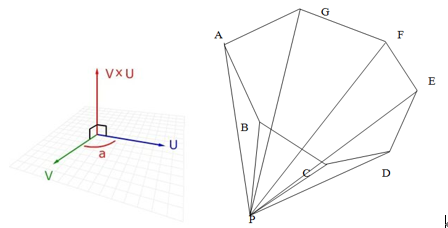
右图中，多边形是逆时针方向，ABCDEFG
第一个三角形：ABP面积为负，为什么呢？AP.cross(BP) 向量的方向是z轴负方向。
最后一个三角形GAP，面积为正，why？GP.cross(AP) 向量的方向是z轴正方向。

结论

多边形顶点顺序为逆时针时，计算的面积为正；顺时针时，面积为负值。

代码

// http://www.cnblogs.com/void/archive/2011/04/17/2018729.html
bool IsPolygonClockWise(const std::vector<Point_Double>& vPolygon)
{
    // compute area of a contour/polygon
    int n = vPolygon.size();

    double A = 0.0;

    for(int p=n-1,q=0; q<n; p=q++)
    {
        A+= vPolygon[p].x * vPolygon[q].y - vPolygon[q].x * vPolygon[p].y;
    }
    double Area = A * 0.5;

    // we want a counter-clockwise polygon in V
    if ( 0.0 < Area )
    {
        return false;
    }
    else
    {
        return true;
    }
}

// http://csharphelper.com/blog/2014/07/calculate-the-area-of-a-polygon-in-c/
bool IsPolygonClockWise_WhenYUp(TXMapPoint* polygon, int count)
{
    double rst = 0.0;

#if 1
    // first point must be equal to last point.
    for (int i = 0; i < count; i++)
    {
        int next = (i + 1) % count;
        double dx = polygon[next].x - polygon[i].x;
        double dy = polygon[next].y + polygon[i].y;
        rst += (dx * dy);

        // overflow issue.
        // rst += ( (polygon[next].x - polygon[i].x) * (polygon[next].y + polygon[i].y) / 2.0 );
    }
#else
    // bad version
    // 没有计算首尾两个点构成的面积。。。
    for (int i = 1; i <count; i++)
    {
        double dx = (polygon[i].x - polygon[i - 1].x);
        double ay = (polygon[i].y + polygon[i - 1].y);
        rst += (dx * ay);
    }
#endif

    if (rst >= 0)
    {
        return true;
    }
    else
    {
        return false;
    }
}

踩过的坑
地图中坐标很大，如果使用int存储，计算面积的时候有越界的可能。越界后结果为负数，也会影响到最终的计算结果。

function 1---------
p   q
2, 0
0, 1
1, 2

2x * 0y - 0x * 2y
0x * 1y - 1x * 0y
1x * 2y - 2x * 1y

function 2---------
(1x - 0x) * (1y + 0y) = 1x * 1y + 1x * 0y - 0x * 1y - 0x * 0y

2x * 2y + 2x * 1y - 1x * 2y - 1x * 1y

(0x - 2x) * (0y + 2y) = 0x * 0y + 0x * 2y - 2x * 0y - 2x * 2y

optim: 
1x * 0y - 0x * 1y
2x * 1y - 1x * 2y
0x * 2y - 2x * 0y
---------

• 第一种方式计算量更加少
• 第二种方式有点冗余，循环中每次的计算结果中有可以抵消的部分
• 第二种优化的结果与第一种正好差一个符号

OpenGL模板测试渲染任意凹多边形

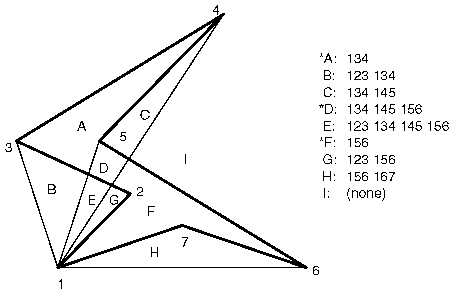
如下图，多边形1234567。A,D,F区域组成了多边形，且这三个区域都是由奇数个三角形覆盖；其他区域由偶数个，或者0个三角形覆盖。如图中右边的列表，B由123,134两个三角形覆盖。

选择任意一点P作为基准点，分别渲染P12，P23，P34，P45，P56，P67，P71 三角形。多边形内部的区域被填充了奇数次，外部的区域被填充了偶数次。
OpenGL渲染凹多边形的思路：借助帧缓冲区，两次渲染多边形的三角形列表。

1. 禁止写入颜色缓冲区，清空帧缓冲区；
2. 遍历三角形渲染，帧缓冲函数采用GL_INVERT。这个函数的效果是，三角形渲染时，它覆盖的每个像素的帧缓冲区值，都在0和非0之间翻转。所有三角形画完，像素被覆盖了偶数次的话，帧缓冲区对应位置的值是0，奇数次的话帧缓冲对应的值是非零。
3. 画一个大多边形，能够包含整个多边形，例如它的boundingbox，但是只允许帧缓冲区中非零的区域通过测试。

点评

• 技术虽有点过时了，这种技术适应任何复杂带洞的多边形渲染。
• 相比较直接凹多边形三角化后渲染，重叠地方的被多次栅格化，性能消耗较大。opengl渲染的步骤，顶点处理，栅格化，片段处理，然后裁剪测试，alpha测试，模板测试（帧缓冲区），深度测试（深度缓冲区）。

ref：http://glprogramming.com/red/chapter14.html#name13