igllib 202_gaussian curvature

the original tutor is like:

there are some points I wanna mention:

1. the discrete Gaussian curvature formula it listed is wrong. How? listen to me explain.

According to the paper "Discrete Differential-Geometry Operators for Triangulated 2-Manifolds" section 4.2, it says

 

In addition, the code also told us about that:

#include <igl/gaussian_curvature.h>
#include <igl/massmatrix.h>
#include <igl/invert_diag.h>
#include <igl/readOFF.h>
#include <igl/viewer/Viewer.h>
#include <igl/jet.h>
#include "tutorial_shared_path.h"

int main(int argc, char *argv[])
{
  using namespace Eigen;
  using namespace std;
  MatrixXd V;
  MatrixXi F;
  igl::readOFF(TUTORIAL_SHARED_PATH "/bumpy.off",V,F);

  VectorXd K;
  // Compute integral of Gaussian curvature
  igl::gaussian_curvature(V,F,K);
  // Compute mass matrix
  SparseMatrix<double> M,Minv;
  igl::massmatrix(V,F,igl::MASSMATRIX_TYPE_DEFAULT,M);
  igl::invert_diag(M,Minv);
  // Divide by area to get integral average, note this line
  K = (Minv*K).eval();

  // Compute pseudocolor
  MatrixXd C;
  igl::jet(K,true,C);

  // Plot the mesh with pseudocolors
  igl::viewer::Viewer viewer;
  viewer.data.set_mesh(V, F);
  viewer.data.set_colors(C);
  viewer.launch();
}

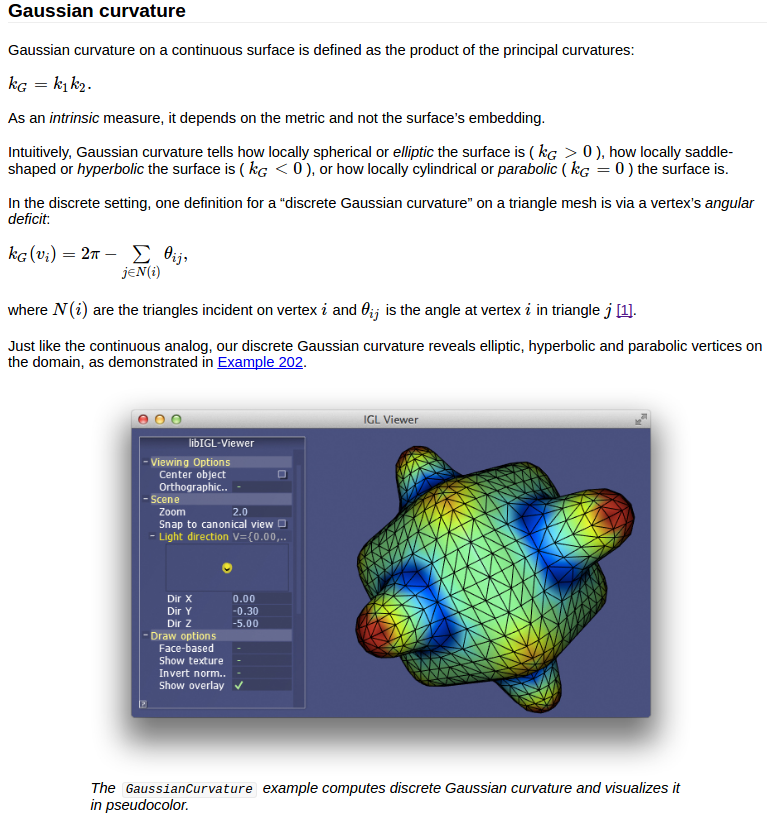
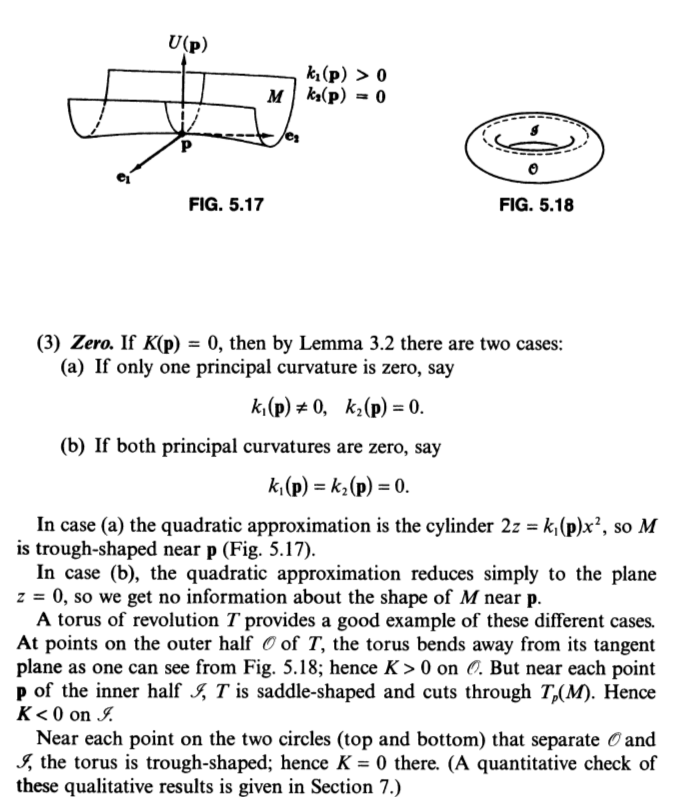
2. I want to offer some material to help readers understand the geometrical meaning