Farthest Point Sampling on 2d image

Farthest Point Sampling的原理是,先随机选一个点,然后呢选择离这个点距离最远的点(D中值最大的点)加入起点,然后继续迭代,直到选出需要的个数为止

其主要代码如下:

%main.m
clear options;
n = 400;
[M,W] = load_potential_map('mountain', n);

npoints_list = round(linspace(20,200,6));%采样点个数列表
landmark = [];
options.verb = 0;
ms = 15;

clf;
for i=1:length(npoints_list)
    nbr_landmarks = npoints_list(i);
    landmark = perform_farthest_point_sampling( W, landmark, nbr_landmarks-size(landmark,2), options );%nbr_landmarks-size(landmark,2) 减去已经存在的点数
    %landmark为已采样的点(包括原来的点和新增的点)
    % compute the associated triangulation
    [D,Z,Q] = perform_fast_marching(W, landmark);
    % display sampling and distance function
    D = perform_histogram_equalization(D,linspace(0,1,n^2));%把D中的值拉到[0,1]范围内
    subplot(2,3,i);
    hold on;
    imageplot(D');
    plot(landmark(1,:), landmark(2,:), 'r.', 'MarkerSize', ms);
    title([num2str(nbr_landmarks) ' points']);
    hold off;
    colormap jet(256);
end

%perform_farthest_point_sampling.m
function [points,D] = perform_farthest_point_sampling( W, points, npoints, options )

% points为已经采样了的点,npoints表示需要加入采样点的个数
% perform_farthest_point_sampling - samples points using farthest seeding strategy
%
% points = perform_farthest_point_sampling( W, points, npoints );
%
%   points can be [] or can be a (2,npts) matrix of already computed 
%       sampling locations.
%   
%   Copyright (c) 2005 Gabriel Peyre

options.null = 0;
if nargin<3
    npoints = 1;
end
if nargin<2
    points = [];
end
n = size(W,1);

aniso = 0;
d = nb_dims(W);
if d==4
    aniso = 1;
    d = 2; % tensor field
elseif d==5
    aniso = 1;
    d = 3; % tensor field
end
s = size(W);
s = s(1:d);

% domain constraints (for shape meshing)
L1 = getoptions(options, 'constraint_map', zeros(s) + Inf );
verb = getoptions(options, 'verb', 1);
mask = not(L1==-Inf);

if isempty(points)
    % initialize farthest points at random
    points = round(rand(d,1)*(n-1))+1;%随机一个点的d维坐标
    % replace by farthest point
    [points,L] = perform_farthest_point_sampling( W, points, 1 );%然后选点到points最远的距离
    Q = ones(size(W));
    points = points(:,end);%取最后一个点,即就是生成的离初始随机点最远的那个点
    npoints = npoints-1;%需要生成的点数减1
else
    % initial distance map
    [L,Q] = my_eval_distance(W, points, options);%如果初始已存在一些采样点,则可以通过perform_fast_marching算距离了, points为初始点(距离为0的点)
%    L = min(zeros(s) + Inf, L1);
%    Q = zeros(s);
end

for i=1:npoints
    if npoints>5 && verb==1
        progressbar(i,npoints);
    end
    options.nb_iter_max = Inf;
    options.Tmax = Inf; % sum(size(W));
    %     [D,S] = perform_fast_marching(W, points, options);
    options.constraint_map = L;
    pts = points;
    if not(aniso)
       pts = pts(:,end);%为何只取最一个点?因为前面的距离都算好了,存储在L中
    end
    D = my_eval_distance(W, pts, options);
    Dold = D;
    D = min(D,L); % known distance map to lanmarks
    L = min(D,L1); % cropp with other constraints
    if not(isempty(Q))
        % update Voronoi
        Q(Dold==D) = size(points,2);
    end
    % remove away data
    D(D==Inf) = 0;
    if isempty(Q)
        % compute farthest points
        [tmp,I] = max(D(:));%找距离最远的点
        [a,b,c] = ind2sub(size(W),I(1));
    else
        % compute farthest steiner point
        [pts,faces] = compute_saddle_points(Q,D,mask);
        a = pts(1,1); b = pts(2,1); c = [];%第1列,为距离D最大的值
        if d==3
            c = pts(3,1);
        end
    end
    if d==2 % 2D
        points = [points,[a;b]];
    else    % 3D
        points = [points,[a;b;c]];
    end    
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [D,Q] = my_eval_distance(W, x, options)%给点权值矩阵W, 初始点x(距离为0的点),则算各点的距离

% D is distance
% Q is voronoi segmentation

options.null = 0;
n = size(W,1);
d = nb_dims(W);

if std(W(:))<eps%即W权值里面值一样
    % euclidean distance
    if size(x,2)>1
        D = zeros(n)+Inf;
        Q = zeros(n);
        for i=1:size(x,2)
            Dold = D; Qold = Q;
            D = min(Dold, my_eval_distance(W,x(:,i)));
            % update voronoi segmentation
            Q(:) = i;
            Q(D==Dold) = Qold(D==Dold);
        end
        return;
    end
    if d==2
        [Y,X] = meshgrid(1:n,1:n);
        D = 1/W(1) * sqrt( (X-x(1)).^2 + (Y-x(2)).^2 );
    else
        [X,Y,Z] = ndgrid(1:n,1:n,1:n);
        D = 1/W(1) * sqrt( (X-x(1)).^2 + (Y-x(2)).^2 + (Z-x(3)).^2 );
    end
    Q = D*0+1;
else
	[D,S,Q] = perform_fast_marching(W, x, options);
end

%perform_fast_marching.m
function [D,S,Q] = perform_fast_marching(W, start_points, options)

% perform_fast_marching - launch the Fast Marching algorithm, in 2D or 3D.
%
%   [D,S,Q] = perform_fast_marching(W, start_points, options)
%
%   W is an (n,n) (for 2D, d=2) or (n,n,n) (for 3D, d=3) 
%       weight matrix. The geodesics will follow regions where W is large.
%       W must be > 0.
%   'start_points' is a d x k array, start_points(:,i) is the ith starting point .
%
%   D is the distance function to the set of starting points.
%   S is the final state of the points : -1 for dead (ie the distance
%       has been computed), 0 for open (ie the distance is only a temporary
%       value), 1 for far (ie point not already computed). Distance function
%       for far points is Inf.(注意对于far来说,1是状态,Inf是距离)
%       (按照书上的说法,-1为known的点,0为trial点,1为far点)
%   Q is the index of the closest point. Q is set to 0 for far points.
%       Q provide a Voronoi decomposition of the domain. 
%
%   Optional:
%   - You can provide special conditions for stop in options :
%       'options.end_points' : stop when these points are reached
%       'options.nb_iter_max' : stop when a given number of iterations is
%          reached.
%   - You can provide an heuristic in options.heuristic (typically that try to guess the distance
%       that remains from a given node to a given target).
%       This is an array of same size as W.
%   - You can provide a map L=options.constraint_map that reduce the set of
%       explored points. Only points with current distance smaller than L
%       will be expanded. Set some entries of L to -Inf to avoid any
%       exploration of these points.
%   - options.values set the initial distance value for starting points
%   (default value is 0).
%
%   See also: perform_fast_marching_3d.
%
%   Copyright (c) 2007 Gabriel Peyre


options.null = 0;

end_points = getoptions(options, 'end_points', []);
verbose = getoptions(options, 'verbose', 1);
nb_iter_max = getoptions(options, 'nb_iter_max', Inf);
values = getoptions(options, 'values', []);
L = getoptions(options, 'constraint_map', []);
H = getoptions(options, 'heuristic', []);
dmax = getoptions(options, 'dmax', Inf);

d = nb_dims(W);

if (d==4 && size(W,3)==2 && size(W,4)==2) || (d==4 && size(W,4)==6) || (d==5 && size(W,4)==3 && size(W,5)==3)
    % anisotropic fast marching
    if d==4 && size(W,3)==2 && size(W,4)==2
        % 2D vector field -> 3D field
        W1 = zeros(size(W,1), size(W,2), 3, 3);
        W1(:,:,1:2,1:2) = W; 
        W1(:,:,3,3) = 1;
        W = reshape(W1, [size(W,1) size(W,2), 1 3 3]);
        % convert to correct size
        W = cat(4, W(:,:,:,1,1), W(:,:,:,1,2), W(:,:,:,1,3), W(:,:,:,2,2), W(:,:,:,2,3), W(:,:,:,3,3) );        
    end
    if d==5
        % convert to correct size
        W = cat(4, W(:,:,:,1,1), W(:,:,:,1,2), W(:,:,:,1,3), W(:,:,:,2,2), W(:,:,:,2,3), W(:,:,:,3,3) );
    end
    
    if size(start_points,1)==2
        start_points(end+1,:) = 1;
    end
    if size(start_points,1)~=3
        error('start_points should be of size (3,n)');
    end
    
    % padd to avoid boundary problem
    W = cat(1, W(1,:,:,:), W, W(end,:,:,:));
    W = cat(2, W(:,1,:,:), W, W(:,end,:,:));
    W = cat(3, W(:,:,1,:), W, W(:,:,end,:));
    
%    if isempty(L)
        L = ones(size(W,1), size(W,2), size(W,3));
 %   end
 
    if dmax==Inf
        dmax = 1e15;
    end
    
%    start_points = start_points-1;
    alpha = 0;
    [D,Q] = perform_front_propagation_anisotropic(W, L, alpha, start_points,dmax);

    % remove boundary problems
    D = D(2:end-1,2:end-1,2:end-1);
    Q = Q(2:end-1,2:end-1,2:end-1);
    S = [];
    D(D>1e20) = Inf;
    return;
end


if d~=2 && d~=3
    error('Works only in 2D and 3D.');
end
if size(start_points,1)~=d
    error('start_points should be (d,k) dimensional with k=2 or 3.');
end

L(L==-Inf)=-1e9;
L(L==Inf)=1e9;
nb_iter_max = min(nb_iter_max, 1.2*max(size(W))^d);

% use fast C-coded version if possible
if d==2
    if exist('perform_front_propagation_2d')~=0
        [D,S,Q] = perform_front_propagation_2d(W,start_points-1,end_points-1,nb_iter_max, H, L, values);
        %讲下vonoroi的分类原理, 假设初始sample点有k个,那么就把这k个sample点作为k个cell的中心,然后将剩下的点距离哪个sample点近就把归于哪个cell里
        %跟那种用平面切出来的cell虽然过程不一样,但是原理是一样的.每一个sample点会拥有一个cell
    else
        [D,S] = perform_front_propagation_2d_slow(W,start_points,end_points,nb_iter_max, H);
        Q = [];
    end
elseif d==3
    [D,S,Q] = perform_front_propagation_3d(W,start_points-1,end_points-1,nb_iter_max, H, L, values);

end
Q = Q+1;

% replace C 'Inf' value (1e9) by Matlab Inf value.
D(D>1e8) = Inf;

运行结果如下:

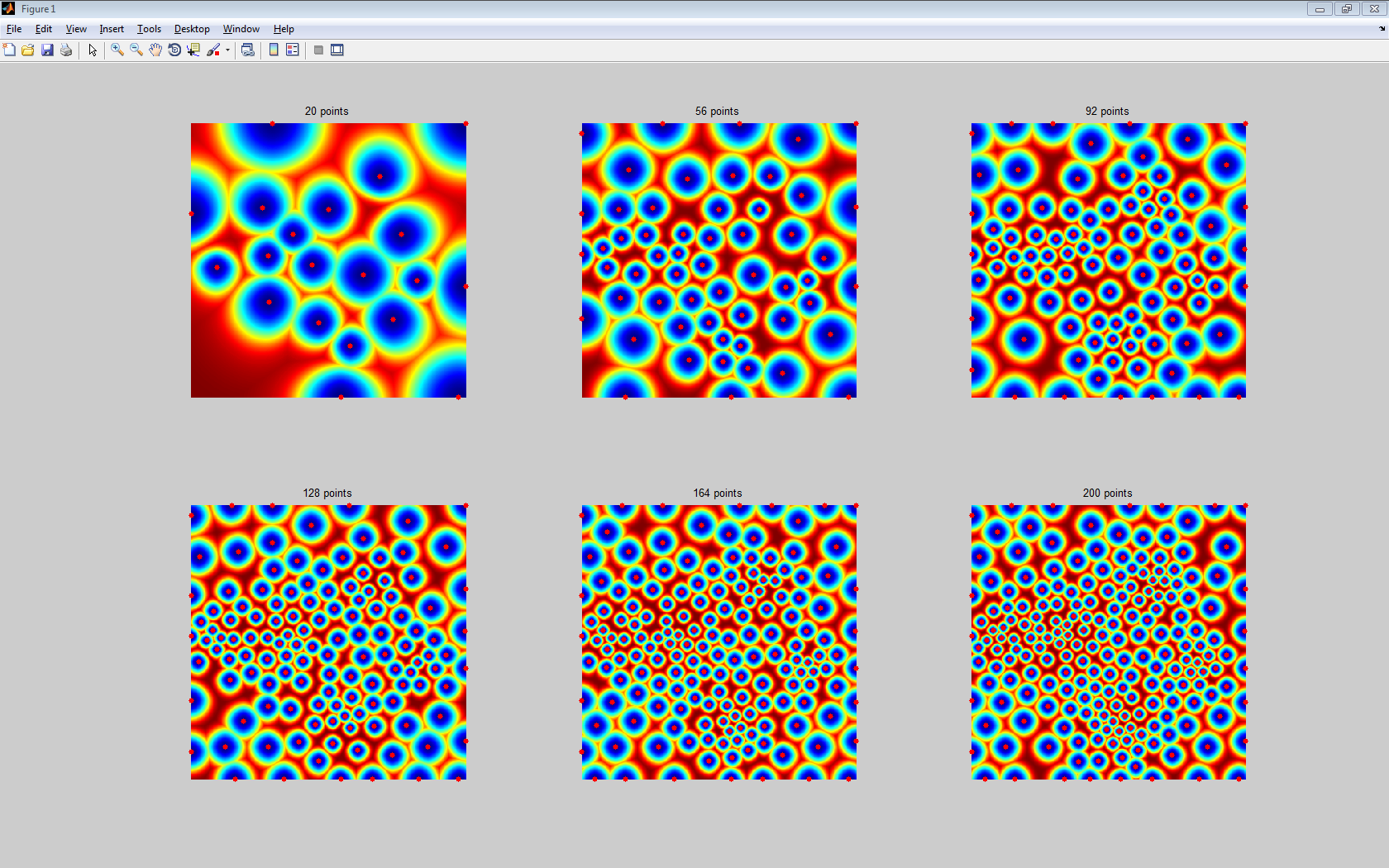
蓝色表示距离为0, 红色表示距离为1.

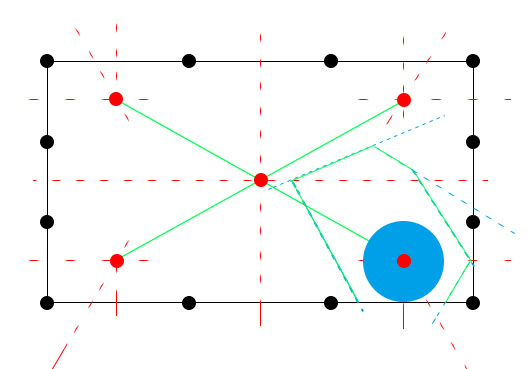
最后讲下该方法与medial axis的共同之处:

1. 最远点一定会落在中轴上面

证明: 最远点是指至少到两个点的距离相等,则此距离最远,那么它肯定满足距离相等这一条件,即它一定会落在中轴上面

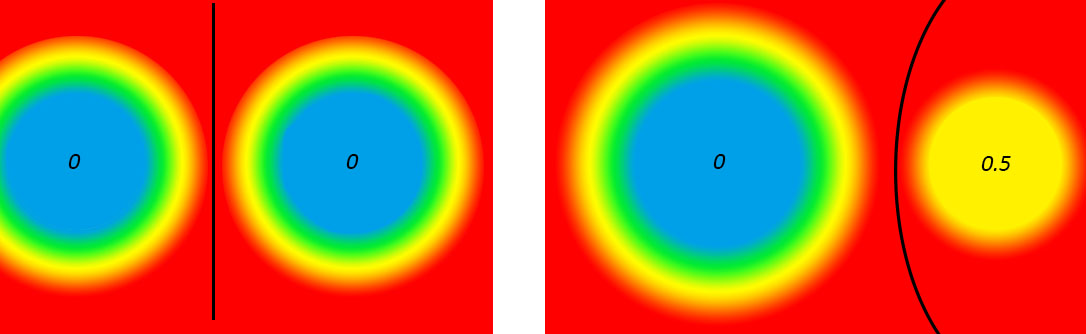
2.它与power diagram的关系为:powder diagram插入球后, 相等于将把weight对应的球的区域设为0.  weight值越小,排斥力越强, 越大,吸引力越强.如果把整个球的区域设为0.5,那么产生的中轴可能就是弧形,而不是直线.而且该弧开是比较靠近值大的球.

matlab完整源代码