文章目录
1.P与NP问题
我们之前就对P与NP问题有所了解。
有些计算问题看起来很难解决。尽管我们进行了多次尝试,但我们仍然不知道这些是否存在高效的算法。然而,我们也无法证明这些问题确实很难解决。我们只是“不知道”或者不确定,至少在目前是这样。用更正式的语言来说,我们不知道P是否等于NP,或者P是否不等于NP。
1.1 计算上难以解决的问题(Hard Computational Problems)
例如前面我们提到的
{
0
,
1
}
\{0,1\}
{0,1}背包问题。
输入:一组物品
{
i
1
,
i
2
,
.
.
.
,
i
n
}
\{i_1,i_2,...,i_n\}
{i1,i2,...,in},其中每个物品
i
j
i_j
ij有一个整数重量
w
j
>
0
w_j>0
wj>0和一个整数收益
b
j
b_j
bj。同时,给定一个最大重量
W
W
W。
目标:找到一个物品的子集,使得这个子集的总重量不超过
W
W
W,并且总收益最大化。注意,不允许取物品的分数部分。
这里我们室友动态规划解决该问题,起时间复杂度是
O
(
n
W
)
O(nW)
O(nW),其中
n
n
n是物体的数量,
W
W
W是背包的最大承重。这个时间复杂度不是多项式时间复杂度,在
W
W
W非常大时仍然会非常慢。动态规划解决方案确实与W的值成线性关系,但与
W
W
W的长度(即W的二进制表示的位数)成指数关系。
例如,如果
W
W
W是
1000000
1000000
1000000,那么W的二进制表示大约是
20
20
20位(因为
2
20
≈
1000000
2^{20} ≈1000000
220≈1000000)。因此,算法的运行时间是
O
(
n
×
2
20
)
O(n×2^{20})
O(n×220),这与W的长度成指数关系。
1.2 决策问题和优化问题(Decision/Optimization problems)
决策问题(Decision problems)指对于一个计算问题,其输出“是”或“否”。换句话说,决策问题的答案是一个布尔值(True或False),表示某个条件是否满足。
优化问题(Optimization problems)中我们的目标是最大化或最小化某个值。
优化问题可以通过添加一个参数
k
k
k来转化为决策问题。具体来说,我们可以通过以下方式将优化问题转化为决策问题:
如果优化问题是最大化某个函数
f
(
x
)
f(x)
f(x),那么可以转化为决策问题:是否存在一个解
x
x
x,使得
f
(
x
)
≥
k
f(x)≥k
f(x)≥k?
如果优化问题是最小化某个函数
f
(
x
)
f(x)
f(x),那么可以转化为决策问题:是否存在一个解
x
x
x,使得
f
(
x
)
≤
k
f(x)≤k
f(x)≤k?
如果一个决策问题是难解的(即没有已知的多项式时间算法),那么其相关的优化问题也必定是难解的。
例如我们前面的
{
0
,
1
}
\{0,1\}
{0,1}背包问题就是一个优化问题,我们的目标是最大化收益函数。因此我们也可以得到其的决策问题版本。
输入:一组物品
{
i
1
,
i
2
,
.
.
.
,
i
n
}
\{i_1,i_2,...,i_n\}
{i1,i2,...,in},其中每个物品
i
j
i_j
ij有一个整数重量
w
j
>
0
w_j>0
wj>0和一个整数收益
b
j
b_j
bj。同时,给定一个最大重量
W
W
W和一个整数
k
k
k。
问题:是否存在一个物品的子集,使得这个子集的总重量不超过
W
W
W,并且总收益至少为
k
k
k?
如果我们可以高效地回答决策问题,那我们就可以高效地解决相关的优化问题。
因此我们通过决策问题的高效解决,我们可以使用二分搜索来找到优化问题的最优解。
具体步骤如下:
- 设定收益的范围,从最小可能收益到最大可能收益。
- 使用二分搜索,在这个范围内查找最大收益,使得决策问题的答案为“是”。
- 每次二分搜索的中间值作为 k k k,询问决策问题。
- 如果决策问题的答案为“是”,则最优解可能在更高的收益范围内;如果答案为“否”,则最优解可能在更低的收益范围内。
- 重复这个过程,直到找到最大收益,使得决策问题的答案为“是”。
1.3 计算问题的正式定义
这一部分的知识与上学期知识类似。
计算问题的输入被编码为有限的二进制字符串
s
s
s。字符串的长度表示为
∣
s
∣
∣s∣
∣s∣。
我们将决策问题与一组字符串联系起来,对于这些字符串,答案是“是”。
我们说算法
A
A
A接受输入字符串
s
s
s,如果
A
A
A在输入
s
s
s上输出“是”。
这个概念可以用上学期的图灵机去理解。现在我们有一个图灵机对算法 A A A是否接受输入字符串 s s s进行判断。它会对接受的字符串 s s s输出“是”。最后决策问题就是包含所有结果为“是”的输入字符串 s s s的集合。
对于某个决策问题
X
X
X,用
L
(
X
)
L(X)
L(X)表示应该被该问题的算法接受的(二进制)字符串的集合。
我们通常将
L
(
X
)
L(X)
L(X)称为一个语言。
这与上学期的知识一致。
我们说算法
A
A
A接受语言
L
(
X
)
L(X)
L(X),如果对于每个字符串
s
∈
L
(
X
)
s∈L(X)
s∈L(X),算法
A
A
A输出“是”;而对于不在
L
(
X
)
L(X)
L(X)中的字符串,算法
A
A
A输出“否”。
下面我们给出
{
0
,
1
}
\{0,1\}
{0,1}背包问题的决策问题版本的形式化语言表达。
首先物品的重量
{
w
i
}
\{w_i\}
{wi}、收益
{
b
i
}
\{b_i\}
{bi}、背包容量
W
W
W和目标值
k
k
k都被编码为二进制字符串。这里一个整数
m
m
m需要
l
o
g
2
m
log_2m
log2m位来表示。
语言
L
(
K
n
a
p
s
a
c
k
)
L(Knapsack)
L(Knapsack):包含所有存在可行解的背包问题实例的编码。
存在一个物品的子集,满足以下条件:
总重量不超过
W
W
W。
总收益至少为
k
k
k。
如果存在这样的子集,那么这个字符串就属于
L
(
K
n
a
p
s
a
c
k
)
L(Knapsack)
L(Knapsack)。
1.4 复杂性类
1.4.1 复杂性类 P P P
复杂性类
P
P
P是包含所有可以用确定性算法在最坏情况下多项式时间内解决的决策问题。
用形式化语言是
P
P
P包含所有可以被多项式时间算法接受的语言
L
(
X
)
L(X)
L(X)(语言
L
(
X
)
L(X)
L(X)即所有“是”的实例集合)。
这些问题可以在
O
(
p
(
n
)
)
O(p(n))
O(p(n))时间内解决,其中
p
(
n
)
p(n)
p(n)是关于输入规模
n
n
n的多项式函数。输入规模通常用
∣
s
∣
∣s∣
∣s∣表示,即输入字符串
s
s
s的长度。
确定性算法是指总是能计算出正确答案的算法。也就是说,存在一个算法
A
A
A,如果
s
∈
L
(
X
)
s∈L(X)
s∈L(X),那么在输入
s
s
s时,算法
A
A
A会在时间
p
(
∣
s
∣
)
p(∣s∣)
p(∣s∣)内输出“是”,其中
∣
s
∣
∣s∣
∣s∣是输入字符串的长度,
p
(
⋅
)
p(⋅)
p(⋅)是一个多项式函数。
直观描述为
P
=
计算机可以快速解决的问题
P = 计算机可以快速解决的问题
P=计算机可以快速解决的问题,也就是这些问题可以通过一个清晰的方法(即多项式时间算法)快速解决。
例如如果一个算法的运行时间是
O
(
n
2
)
O(n^2)
O(n2)或
O
(
n
3
)
O(n^3)
O(n3),那么它就是多项式时间算法。
现在我们给出复杂性类
P
P
P的几个问题示例。
- 分数背包问题(Fractional Knapsack Problem)
- 带非负边权的图中的最短路径问题(Shortest Paths in Graphs with Non-negative Edge Weights)
- 任务调度问题(Task Scheduling)
1.4.2 证明(Certification)
找到决策问题的解决方案可能很难,但是验证解决方案是相对简单的。
例如数独(Sudoku)问题。
数独问题给定一个
n
2
×
n
2
n^2×n^2
n2×n2的数组,该数组被划分为n×n的方块。数组中的一些单元格已经填入了介于
1...
n
2
1...n^2
1...n2范围内的整数。
目标是完成数组,使得每一行、每一列和每个方块都包含从
1...
n
2
1...n^2
1...n2的所有整数。
找到数独问题的解决方案可能很困难,因为需要尝试不同的组合并满足所有约束条件。
然而,一旦找到一个解决方案,验证它是否正确却相对容易,因为只需要检查每一行、每一列和每个子网格是否包含从
1...
n
2
1...n^2
1...n2的所有整数,而不重复。

因此我们现在回到前面的
{
0
,
1
}
\{0,1\}
{0,1}背包问题。
给定一组物品的重量、收益,以及参数
W
W
W(背包的最大容量)和
k
k
k(目标收益),如果提出一个这些物品的子集,可以很容易地检查这些物品的总重量是否不超过
W
W
W,以及总收益是否至少为
k
k
k。
如果这两个条件都满足,那么我们说这个物品子集是决策问题的一个证明(certificate),即它验证了
{
0
,
1
}
\{0,1\}
{0,1}背包决策问题的答案是“是”。
有效证明的概念是用来定义NP问题类的。NP(Nondeterministic Polynomial time)问题类包含所有可以在多项式时间内验证解的决策问题。
1.4.3 复杂性类NP
NP类包含所有存在有效证明者的决策问题。
这里的“有效证明者”指的是可以在多项式时间内验证解的算法。更正式的定义如下:
对于一个决策问题
X
X
X,有效证明者是一个算法
B
B
B,它接受两个输入字符串
s
s
s和
t
t
t。
字符串
s
s
s是决策问题的输入。
“有效”意味着
B
B
B是一个多项式时间算法,即存在一个多项式函数
q
(
⋅
)
q(⋅)
q(⋅),对于所有字符串,我们有
s
∈
L
(
X
)
s∈L(X)
s∈L(X)当且仅当存在一个字符串
t
t
t,使得
∣
t
∣
≤
q
(
∣
s
∣
)
∣t∣≤q(∣s∣)
∣t∣≤q(∣s∣)且
B
(
s
,
t
)
=
“是”
B(s,t)=“是”
B(s,t)=“是”。
这里
∣
t
∣
≤
q
(
∣
s
∣
)
∣t∣≤q(∣s∣)
∣t∣≤q(∣s∣)的意思是:证明
t
t
t的长度必须被一个关于输入
s
s
s长度的多项式函数
q
(
⋅
)
q(⋅)
q(⋅)所限制。换句话说,那就是证明不会随着输入的增长而呈指数级增加。
我们可以将字符串
t
t
t视为决策问题答案为“是”的“证明”。换句话说,如果存在这样的字符串
t
t
t,那么它就证明了输入字符串
s
s
s属于语言
L
(
X
)
L(X)
L(X)。
下面给出例子。
COMPOSITE问题:给定一个整数
s
s
s,判断
s
s
s是否为合数(即不是质数)。
如果存在一个整数
t
t
t(满足
1
<
t
<
s
1<t<s
1<t<s),使得
s
s
s是
t
t
t的倍数,那么
s
s
s就是合数。
在这里YES实例
s
=
437
,
669
s=437,669
s=437,669。
我们的证明
t
=
541
或
809
t=541或809
t=541或809。
因为
437
,
669
=
541
×
809
437,669=541×809
437,669=541×809。
所以我们回到前面的定义检查以下,这里
s
=
437
,
669
∈
L
(
X
)
s=437,669∈L(X)
s=437,669∈L(X),因为
437
,
669
437,669
437,669是合数。然后我们用
437
,
669
/
541
437,669/541
437,669/541能很快地出结果,这一步的算法是多项式复杂度的。这里有效证明者做的是检查
t
t
t是否满足
1
<
t
<
s
1<t<s
1<t<s并验证
s
s
s是否能被
t
t
t整除。
我们再举一个NO实例
s
=
437
,
677
s=437,677
s=437,677。所以我们这里
B
(
s
,
t
)
=
“是”
B(s,t)=“是”
B(s,t)=“是”。
对于这个实例,我们不存在任何证明(Certificate)可以欺骗验证者使其错误地判断该实例属于语言
L
(
X
)
L(X)
L(X)。

我们现在对YES实例和NO实例有了更清楚的理解。
YES实例:存在一个证明(Certificate),使得验证者可以确认该实例属于语言
L
(
X
)
L(X)
L(X)。
NO实例:不存在任何证明(Certificate)可以欺骗验证者使其错误地判断该实例属于语言
L
(
X
)
L(X)
L(X)
1.4.4 非确定性算法(non-deterministic algorithm)
非确定性算法是在执行过程中可以执行任意数量的非确定性分支的算法。
这种算法在其中一个分支结束时终止。

非确定性分支指的是算法在某个步骤可以同时探索多个可能的选择,而不是只选择一个。
这种选择不是真正并行执行的,而是一种理论上的构造,用于描述算法可能探索的所有可能路径。
我们现在给出NP问题类的另一种定义。NP问题类是可以在多项式时间内非确定性地接受(即找到解决方案)的决策问题
X
X
X(或语言
L
(
X
)
L(X)
L(X))的集合。
非确定性计算机是一种理论上的计算模型,它可以“猜测”正确的答案或解决方案。
NP问题也可以被看作是那些解决方案可以在多项式时间内被验证的问题类。
对于输入字符串
s
s
s,非确定性算法可以生成一个多项式长度的字符串
t
t
t(作为解决方案的“证明”或“证书”)。
然后,我们使用算法
B
B
B来检查
B
(
s
,
t
)
=
“是”
B(s,t)=“是”
B(s,t)=“是”。
重要的是,如果答案是“是”,则算法
B
B
B将在多项式时间内以该输出终止。
现在我们回到我们贯穿始终的例子
{
0
,
1
}
\{0,1\}
{0,1}背包问题。
给定一组物品
I
=
{
i
1
,
i
2
,
.
.
.
,
i
n
}
I=\{i_1,i_2,...,i_n\}
I={i1,i2,...,in},每个物品
i
j
i_j
ij有一个正整数重量
w
j
w_j
wj和一个整数收益
b
j
b_j
bj。另外,给定一个最大重量
W
W
W和一个整数
k
k
k。
假设有人提出了一个物品的子集,我们可以很容易地检查(有效验证者):
- 这些物品的总重量是否不超过 W W W;
- 总价值是否至少为 k k k。
如果这两个条件都满足,那么这个物品子集就是一个证明(certificate)
t
t
t,用于验证
{
0
,
1
}
\{0,1\}
{0,1}背包决策问题的答案是“是”。
算法
B
(
s
,
t
)
B(s,t)
B(s,t)=“是”意味着算法
B
B
B接收输入字符串
s
s
s(表示背包问题的实例)和证明
t
t
t(表示提出的解),并验证这个解是否正确。
我们需要注意这里输入
s
s
s表示整个背包问题的实例,包括所有物品的重量集合、所有物品的收益集合、背包的最大容量
W
W
W和目标收益
k
k
k。
而证明
t
t
t表示提出的一个可能的解决方案,即一个物品的子集。
满足条件的物品子集是可行解,而不是必然是最优解。最优解是指在所有可行解中收益最大的解,这通常涉及到更复杂的计算和比较。
在NP问题的定义中,我们关注的是是否存在至少一个可行解,而不是找到最优解。
所以我们现在再总结一下这里的概念。
- 算法
A
A
A(决策算法):
算法 A A A旨在确定输入 s s s是否属于语言 L ( K n a p s a c k ) L(Knapsack) L(Knapsack)。
它通过搜索有效物品子集直接解决问题。 - 算法
B
B
B(验证算法):
算法 B B B是一个验证器(证明者),用于检查给定的物品子集 t t t(证书)是否是输入 s s s的有效解决方案。 - 非确定性算法:
{ 0 , 1 } \{0,1\} {0,1}背包问题的非确定性算法涉及猜测一个物品子集并使用算法 B B B进行验证。 - 证书
t
t
t:
提出的物品子集,作为输入 s s s属于 L ( K n a p s a c k ) L(Knapsack) L(Knapsack)的证据。 - 输入字符串
s
s
s:
s s s是输入字符串,表示整个背包问题的实例。 - 语言
L
(
K
n
a
p
s
a
c
k
)
L(Knapsack)
L(Knapsack):
包含所有存在可行解的背包问题实例的编码。
现在我们给出一个例子。
假设我们有一个具体的
{
0
,
1
}
\{0,1\}
{0,1}背包问题实例,其中包含
3
3
3个物品,每个物品的重量和收益分别为
{
2
,
3
,
4
}
\{2,3,4\}
{2,3,4} 和
{
3
,
4
,
5
}
\{3,4,5\}
{3,4,5},背包的最大容量为
5
5
5,目标收益为
7
7
7。这个实例的二进制编码可能如下:
w
1
=
2
w_1=2
w1=2 → 二进制编码为
10
10
10。
w
2
=
3
w_2=3
w2=3 → 二进制编码为
11
11
11。
w
3
=
4
w_3=4
w3=4 → 二进制编码为
100
100
100。
b
1
=
3
b_1=3
b1=3 → 二进制编码为
11
11
11。
b
2
=
4
b_2=4
b2=4 → 二进制编码为
100
100
100。
b
3
=
5
b_3=5
b3=5 → 二进制编码为
101
101
101。
W
=
5
W=5
W=5 → 二进制编码为
101
101
101。
k
=
7
k=7
k=7 → 二进制编码为
111
111
111。
将这些编码组合成一个字符串,例如:
10
,
11
,
100
,
11
,
100
,
101
,
101
,
111
10,11,100,11,100,101,101,111
10,11,100,11,100,101,101,111。这个字符串
s
s
s就是输入,它编码了整个背包问题的实例。而这个
s
s
s属于
L
(
K
n
a
p
s
a
c
k
)
L(Knapsack)
L(Knapsack),因为存在
t
t
t满足
B
(
s
,
t
)
=
“是”
B(s,t)=“是”
B(s,t)=“是”。
1.4.5 P和NP的关系:
P
⊆
N
P
P⊆NP
P⊆NP:P是NP的一个子集。这意味着所有可以在多项式时间内解决的问题(P类问题)也可以在多项式时间内验证解(因此也是NP问题)。
P问题:可以在多项式时间内解决的问题。这些问题被认为是“容易”的,因为它们可以快速找到解决方案。
NP问题:如果给定一个解决方案,可以在多项式时间内验证的问题。这些问题可能很难找到解决方案,但如果给定一个潜在的解决方案,可以快速验证其正确性。
如果一个问题属于P类(可以在多项式时间内解决),那么它的解决方案也可以在多项式时间内使用相同的算法进行验证。
P
=
N
P
P = NP
P=NP还是
P
≠
N
P
P ≠ NP
P=NP:
这是计算复杂性理论中最著名的未解决问题之一。数学家和计算机科学家目前不知道P是否等于NP,还是P不等于NP。尽管多项式时间内的可验证性看起来是比多项式时间内的可解性更弱的条件。

2. NP-Completeness(NP完全性)
2.1 布尔电路(Boolean Circuit)
布尔电路是一种有向图,其中每个顶点(称为逻辑门)对应于一个简单的布尔函数,如AND(与)、OR(或)或NOT(非)。
输入边(Incoming edges):指向逻辑门的边,表示该逻辑门的输入。
输出边(Outgoing edges):从逻辑门出发的边,表示该逻辑门的输出。

示例如下图所示。

2.2 Circuit-SAT问题
这里SAT 代表可满足性(Satisfiability)。
输入:一个具有单个输出顶点的布尔电路。
问题:是否存在一种输入值的赋值方式,使得布尔电路的输出值为
1
1
1?
非确定性算法:非确定性算法选择一种输入位的赋值方式,并确定性地检查这种输入是否会产生输出值为
1
1
1。
示例如下图所示。

这里有多种满足的结果。
因此Circuit-SAT问题的完整表达是给定一个具有单个输出节点的布尔电路,是否存在一种输入值的赋值方式,使得输出值为 1 1 1?
这里的Circuit-SAT属于NP问题类的证明如下:
猜测:非确定性算法为所有输入以及每个逻辑门的输出猜测值。
验证:验证每个逻辑门的输出(我们猜测的)是否与其基于输入的布尔函数(AND、OR、NOT)相匹配。这种验证相对于电路大小在多项式时间内完成。
接受条件:如果所有门都与其布尔函数一致,并且最终输出为1,则接受该解决方案。
由于解决方案可以在多项式时间内被验证,因此Circuit-SAT属于NP问题类。
2.3 顶点覆盖问题(Vertex Cover,VC)
顶点覆盖是指给定一个图
G
=
(
V
,
E
)
G=(V,E)
G=(V,E),其中
V
V
V是顶点集,
E
E
E是边集。
顶点覆盖是
V
V
V的一个子集
C
⊆
V
C⊆V
C⊆V,使得对于
E
E
E中的每条边
(
v
,
w
)
(v,w)
(v,w),至少有一个顶点
v
v
v或
w
w
w在
C
C
C中。
图和顶点覆盖示例如下。

优化问题版本:寻找尽可能小的顶点覆盖,即找到一个最小的顶点集合
C
C
C,使得
C
C
C是图
G
G
G的一个顶点覆盖。
决策问题版本:给定一个图
G
G
G和一个整数
k
k
k,询问是否存在一个包含最多
k
k
k个顶点的顶点覆盖。
这里的决策问题属于NP问题类的证明如下:
猜测:一个非确定性算法猜测
V
V
V的一个子集
C
C
C,其大小最多为
k
k
k。这意味着我们从图
G
G
G中选择最多
k
k
k个顶点。
验证:首先检查
∣
C
∣
≤
k
∣C∣≤k
∣C∣≤k。然后验证对于每条边
(
u
,
v
)
∈
E
(u,v)∈E
(u,v)∈E,至少有一个顶点
u
u
u或
v
v
v在
C
C
C中。这种验证相对于边的数量在多项式时间内完成。
接受条件:如果
∣
C
∣
≤
k
∣C∣≤k
∣C∣≤k并且所有边都通过了这个检查,则接受该解决方案。
由于解决方案可以在多项式时间内被验证,顶点覆盖问题属于NP问题类。
2.4 多项式时间可归约性(Polynomial-time reducibility)
多项式时间可归约性(Polynomial-time reducibility)对于确定一个问题是否为NP完全问题是重要的。
一个决策问题
L
L
L可以在多项式时间内归约到另一个多项式时间问题
M
M
M(记作
L
→
poly
M
L \overset{\text{poly}}{\rightarrow} M
L→polyM),如果存在一个可以在多项式时间内计算的函数
f
f
f,满足以下条件:
将
L
L
L的任何输入
s
s
s转换为
M
M
M的输入
f
(
s
)
f(s)
f(s)。
s
s
s是
L
L
L的“是”实例当且仅当
f
(
s
)
f(s)
f(s)是
M
M
M的“是”实例。
归约的意义主要是:
- 如果 M M M可以在多项式时间内解决,那么 L L L也可以。
- 如果
L
L
L是难解的(即没有已知的多项式时间算法),那么
M
M
M也必须是难解的。
这两点都是因为归约可以证明 M M M至少和 L L L一样难。
我们使用 L → poly M L \overset{\text{poly}}{\rightarrow} M L→polyM表示语言 L L L可以在多项式时间内归约到语言 M M M。
2.4.1 NP-hard
如果一个决策问题定义的语言 M M M是NP-hard的,那么NP中的每一个其他语言 L L L都可以在多项式时间内归约到 M M M。这意味着对于NP中的每一个 L L L,都存在一个多项式时间可计算的函数 f f f,使得 L → poly M L \overset{\text{poly}}{\rightarrow} M L→polyM。
如果一个语言
M
M
M是NP-hard的,并且它本身也属于NP(即可以在多项式时间内解决),那么
M
M
M就是NP完全的(NP-complete)。
NP完全问题是NP中最难的问题之一。如果能够解决任何一个NP完全问题,那么理论上也能在多项式时间内解决所有NP问题。
P问题:可以在多项式时间内解决的决策问题。形式上,如果一个问题可以在
O
(
n
k
)
O(n^k)
O(nk)时间内解决,其中
n
n
n是输入的大小,
k
k
k是某个常数,则该问题属于P类。
NP问题:给定一个解决方案,可以在多项式时间内验证其正确性的决策问题。
NP-Hard问题:至少和NP问题中最难的问题一样难的问题。NP中的每个问题都可以在多项式时间内归约到NP-Hard问题。值得注意的是,NP-Hard问题可能不属于NP类,因为它们可能比NP问题更难(例如,停机问题)或者无法在多项式时间内验证解。
NP-Complete问题:同时满足以下两个条件的问题:
- NP-Hard(所有NP问题都可以归约到这些问题)。
- 属于NP(解决方案可以在多项式时间内被验证)。
因此,NP完全问题是NP-hard问题集合和NP问题集合的交集。
下面的图展示了这些问题的关系。

NP完全问题被描述为NP问题类中“最难”的问题。
所以如果一个NP完全问题可以在多项式时间内解决,那么NP中的所有问题都可以在多项式时间内解决,因此P等于NP。
2.5 合取范式(Conjunctive Normal Form,简称CNF)
一个布尔公式如果由多个子句(clauses)组成,这些子句使用逻辑与(AND,表示为
∧
∧
∧)连接,而每个子句内部的字面量(literals,即变量
x
i
x_i
xi或其否定
x
i
‾
\overline{x_i}
xi)使用逻辑或(OR,表示为
∨
∨
∨)连接,则称该公式处于合取范式。
下面给出一些例子。
(
x
1
‾
∨
x
2
‾
∨
x
4
∨
x
6
‾
)
∧
(
x
2
‾
∨
x
4
∨
x
5
‾
∨
x
3
)
(\overline{x_1} \lor \overline{x_2} \lor x_4 \lor \overline{x_6}) \land (\overline{x_2} \lor x_4 \lor \overline{x_5} \lor x_3)
(x1∨x2∨x4∨x6)∧(x2∨x4∨x5∨x3)
( x 2 ∨ x 3 ‾ ∨ x 1 ‾ ) ∧ ( x 1 ∨ x 3 ∨ x 4 ) ∧ ( x 4 ‾ ∨ x 2 ‾ ∨ x 5 ‾ ) (x_2 \lor \overline{x_3} \lor \overline{x_1}) \land (x_1 \lor x_3 \lor x_4) \land (\overline{x_4} \lor \overline{x_2} \lor \overline{x_5}) (x2∨x3∨x1)∧(x1∨x3∨x4)∧(x4∨x2∨x5)
( x 2 ‾ ∨ x 1 ) ∧ ( x 1 ‾ ∨ x 4 ∨ x 3 ) ∧ ( x 4 ∨ x 3 ) ∧ ( x 3 ‾ ∨ x 2 ∨ x 5 ‾ ∨ x 1 ‾ ) (\overline{x_2} \lor x_1) \land (\overline{x_1} \lor x_4 \lor x_3) \land (x_4 \lor x_3) \land (\overline{x_3} \lor x_2 \lor \overline{x_5} \lor \overline{x_1}) (x2∨x1)∧(x1∨x4∨x3)∧(x4∨x3)∧(x3∨x2∨x5∨x1)
2.6 CNF-SAT(Conjunctive Normal Form Satisfiability)问题
这是布尔可满足性问题(SAT)的一个特定变体,其中布尔公式以合取范式(CNF)给出。
输入:一个以合取范式(CNF)表示的布尔公式
C
C
C。
公式
C
C
C由多个子句(clauses)通过逻辑与(AND,表示为
∧
∧
∧)连接组成:
C
=
c
1
∧
c
2
∧
.
.
.
∧
c
n
C=c_1∧c_2∧...∧c_n
C=c1∧c2∧...∧cn,其中每个子句
c
i
c_i
ci是一个字面量(literal)的逻辑或(OR,表示为
∨
∨
∨)的组合。每个字面量可以是一个变量
x
k
x_k
xk或其否定
x
k
‾
\overline{x_k}
xk。变量表示为
x
1
,
x
2
,
.
.
.
,
x
n
x_1,x_2,...,x_n
x1,x2,...,xn。
问题:是否存在一种布尔值(真/假)的赋值方式给变量
x
1
,
x
2
,
.
.
.
,
x
n
x_1,x_2,...,x_n
x1,x2,...,xn
,使得整个公式
C
C
C计算结果为真(即每个子句
c
i
c_i
ci至少有一个字面量为真)?
2.6.1 库克-列文定理(Cook-Levin Theorem)
库克-列文定理表明布尔电路可满足性问题(Circuit-SAT)是NP完全的。
证明过程如下:
步骤1:证明Circuit-SAT属于NP问题类。
证明:通过计算有限数量的逻辑门的输出来验证输入赋值是否满足电路,其中之一将是电路的输出。这可以在多项式时间内完成。因此,根据NP的定义,Circuit-SAT属于NP。
步骤2:证明Circuit-SAT属于NP-Hard,所以现在要说明对于NP中的每一个问题
L
L
L,都存在一个多项式时间可计算的函数,使得
L
L
L可以归约到Circuit-SAT。
证明:任何NP问题
L
L
L都有一个多项式时间的验证器
V
V
V(一个图灵机或算法)。
在输入
s
s
s和证书
t
t
t上,算法
B
B
B(
V
V
V)的计算可以被编码为一个布尔电路
C
s
C_s
Cs。
归约:如果
s
∈
L
s∈L
s∈L,那么存在一个证书
t
t
t使得
C
s
(
t
)
=
T
r
u
e
C_s(t)=True
Cs(t)=True。
反之,如果
C
s
C_s
Cs是可满足的,那么
s
∈
L
s∈L
s∈L。
构建
C
s
C_s
Cs的过程需要多项式时间(因为
V
V
V的计算是多项式的)。
因此,Circuit-SAT是NP-Hard的。
所以我们获得了推论:合取范式可满足性问题(CNF-SAT)是NP完全(NP-complete)的。
由于任何布尔电路都可以转换为等价的合取范式(CNF)公式,并且布尔电路可满足性问题(Circuit-SAT)是NP完全的,因此可以推断出CNF-SAT也是NP完全的。
这意味着即使在SAT问题的一个受限形式中,即公式以合取范式(CNF)给出时,它仍然是NP-hard的,同时显然属于NP。
2.6.2 NP完全性的证明
根据上面的这个定理的证明过程,我们现在知道如何证明一个新的问题 X X X是 NP完全的。
- 首先,证明
X
∈
N
P
X∈NP
X∈NP:
这意味着需要展示问题 X 有一个多项式时间的非确定性算法,或者等价地,展示 X 有一个有效的验证器(certifier)。
验证器是一个能在多项式时间内验证给定解是否正确的算法。 - 其次,选择一个已知的 NP完全问题 Y Y Y,并展示从 Y Y Y到 X X X的多项式时间归约:这意味着需要展示 Y → poly X Y \overset{\text{poly}}{\rightarrow} X Y→polyX,即对于 Y Y Y中的每个实例,都可以在多项式时间内构造出一个对应的 X X X实例,使得 Y Y Y实例的解与 X X X实例的解等价。(也就是证明 X X X是NP-hard的)
我们现在介绍一个引理,或者说归约的传递性:如果 L 1 L_1 L1可以在多项式时间内归约到 L 2 L_2 L2,且 L 2 L_2 L2可以在多项式时间内归约到 L 3 L_3 L3,那么 L 1 L_1 L1也可以在多项式时间内归约到 L 3 L_3 L3。
现在我们可以尝试将前面的顶点覆盖问题(VC)归约到合取范式可满足性问题(CNF-SAT)。
证明步骤如下:
对于图中的每个顶点
i
i
i,引入一个布尔变量
v
i
v_i
vi,如果顶点
v
i
v_i
vi在覆盖集
C
C
C中,则
v
=
1
i
v_=1i
v=1i
对于每条边
(
i
,
j
)
∈
E
(i,j)∈E
(i,j)∈E,至少有一个端点必须在覆盖中。这可以通过子句
(
v
i
∨
v
j
)
(v_i∨v_j)
(vi∨vj)来编码。
整个覆盖条件是所有这些子句的逻辑与(AND):
⋀
(
i
,
j
)
∈
E
(
v
i
∨
v
j
)
⋀ (i,j)∈E(v_i∨v_j)
⋀(i,j)∈E(vi∨vj)。
我们需要确保顶点覆盖中顶点的数量最多为
k
k
k。这可以通过使用加法布尔电路(adder Boolean circuits)和等式电路(equality circuits)来完成这个验证过程。
这种构造可以在多项式时间内完成。
归约:如果图
G
G
G有一个大小不超过
k
k
k 的顶点覆盖
C
C
C,则设置
v
i
=
1
v_i=1
vi=1对于
i
∈
C
i∈C
i∈C,否则
v
i
=
0
v_i=0
vi=0满足所有边子句。
反之,一个满足的赋值给出了一个大小不超过
k
k
k的顶点覆盖
C
=
i
∣
v
i
=
1
C={i∣v_i=1}
C=i∣vi=1。
2.6.3 3-SAT(3可满足性问题)
输入:一个CNF形式的布尔公式
C
=
c
1
∧
c
2
∧
.
.
.
∧
c
n
C=c_1∧c_2∧...∧c_n
C=c1∧c2∧...∧cn其中子句
c
i
c_i
ci依赖于变量
x
1
∧
x
2
∧
.
.
.
∧
x
m
x_1∧x_2∧...∧x_m
x1∧x2∧...∧xm,并且每个子句
c
i
c_i
ci形式为
x
i
1
∨
x
i
2
∨
x
i
3
x_{i1}∨x_{i2}∨x_{i3}
xi1∨xi2∨xi3,其中
1
≤
i
≤
m
1≤i≤m
1≤i≤m。
问题:是否存在一种变量
x
i
x_i
xi的真值赋值方式,使得公式
C
C
C可满足(即最后的结果为真,或者说每个子句的结果都为真)?
3-SAT是CNF-SAT问题的一个特例,其中每个子句恰好包含三个文字量(literals)。
所以3-SAT也是NP完全的。
2.6.4 团问题(Clique问题)
团(Clique)是图的一个子图,它是一个完全图。完全图是指图中的每个节点至少通过一条边与其他所有节点相连。
问题:给定一个图
G
G
G,问题是判断
G
G
G中是否存在一个包含
k
k
k个节点的完全子图(即
k
k
k-团)。
团问题也是NP完全的。
2.6.5 独立集问题(Independent Set)
给定一个图
G
=
(
V
,
E
)
G=(V,E)
G=(V,E),其中
V
V
V是顶点集,
E
E
E是边集,独立集
S
S
S是
V
V
V中的一组顶点,这组顶点中任意两个顶点都不相邻(即图中不存在连接这两个顶点的边)。
问题:是否存在一个至少包含
k
k
k个顶点的独立集。
独立集问题也是NP完全的
2.6.6 NP完全问题的总结
NP完全问题有:
-
{ 0 , 1 } \{0,1\} {0,1}背包问题
-
Circuit-SAT问题
-
CNF-SAT问题
-
3-SAT问题
-
VC问题
-
Clique问题
-
Independent Set问题
-
Feedback Arc Set(反馈弧集):
在有向图中,反馈弧集问题是找到最小的弧集合,移除这些弧后使得图不再包含任何有向环(即变得无环)。 -
Hamiltonian Cycle(哈密顿回路):
哈密顿回路问题是确定一个图中是否存在一个回路,该回路恰好访问每个顶点一次并返回起始顶点。 -
Max Cut(最大割):
最大割问题是在一个无向图中找到一个顶点的划分,使得划分产生的两个子图之间的边的权重之和最大。 -
Subset Sum(子集和):
子集和问题是确定一个整数集合是否有一个子集,其元素之和等于给定的目标和。 -
Integer Programming(整数规划):
整数规划是线性规划的一个子类,其中要求解决方案中的变量是整数。这包括了各种优化问题,如找到一组物品的最优组合,满足特定的约束条件。
还有其他NP完全问题。
2.7 系统证明VC问题是NP完全的
我们现在系统的证明一下VC问题是NP完全的。
证明步骤如下:
步骤1:VC属于NP。(也就是展示问题有一个多项式时间的非确定性算法,或者等价地,展示问题有一个有效的验证器)
要证明VC属于NP,需要展示给定一个候选解(一个顶点的子集
S
S
S),我们可以在多项式时间内验证
S
S
S是否是大小最多为
k
k
k的顶点覆盖。
验证过程:首先检查
∣
S
∣
≤
k
∣S∣≤k
∣S∣≤k:计算
S
S
S中的顶点数量并与
k
k
k比较,这需要
O
(
∣
V
∣
)
O(∣V∣)
O(∣V∣)时间。
对于图中的每条边
(
u
,
v
)
∈
E
(u,v)∈E
(u,v)∈E,检查
u
∈
S
u∈S
u∈S或
v
∈
S
v∈S
v∈S:这需要检查最多
∣
E
∣
∣E∣
∣E∣条边,每条边检查需要
O
(
1
)
O(1)
O(1)时间。
因此,总的验证时间是
O
(
∣
V
∣
+
∣
E
∣
)
O(∣V∣+∣E∣)
O(∣V∣+∣E∣),这是多项式时间。
因此,VC属于NP。
步骤2:从已知的NP完全问题归约到VC,这里我们使用3-SAT,也就是3-SAT到VC的归约。
归约目标:在多项式时间内,构造一个图和一个顶点数量
k
k
k,使得存在一个大小为
k
k
k的顶点覆盖当且仅当3-SAT公式可满足。
对于给定的3-SAT公式
ϕ
ϕ
ϕ,其中包含
m
m
m个子句
C
1
,
.
.
.
,
C
m
C_1,...,C_m
C1,...,Cm和
n
n
n个变量
x
1
,
.
.
.
,
x
n
x_1,...,x_n
x1,...,xn,构造图
G
G
G的方式如下:
例如我们现在有一个3-SAT公式
ϕ
ϕ
ϕ有两个变量和三个子句。
ϕ
=
(
x
1
∨
x
2
∨
x
2
)
∧
(
x
1
‾
∨
x
2
‾
∨
x
2
‾
)
∧
(
x
1
‾
∨
x
2
∨
x
2
)
ϕ= (x_1 \lor x_2 \lor {x_2}) \land ( \overline{x_1} \lor \overline{x_2} \lor \overline{x_2}) \land (\overline{x_1} \lor x_2 \lor {x_2})
ϕ=(x1∨x2∨x2)∧(x1∨x2∨x2)∧(x1∨x2∨x2)
我们创建一个特殊的子图结构(Variable Gadget):
每个变量
x
i
x_i
xi创建两个顶点
x
i
x_i
xi和
x
i
‾
\overline{x_i}
xi并且用一条边连接它们。任一顶点覆盖必须包含至少两个顶点中的一个顶点以覆盖这条边。
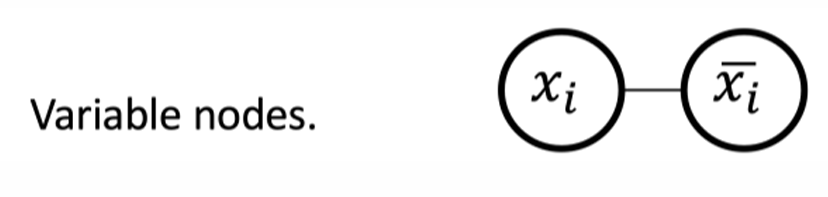
也就是对于每个变量对应的gadget(即每个变量的子图结构),我们必须恰好选择一个节点来包含在我们的顶点覆盖中。
我们再构造另一种特殊子图(Clause Gadget):
对于每个子句
C
j
=
(
l
j
1
∨
l
j
2
∨
l
j
3
)
C_j=(l_{j_1}∨l_{j_2}∨l_{j_3})
Cj=(lj1∨lj2∨lj3),创建一个由三个顶点
v
j
1
,
v
j
2
,
v
j
3
v_{j_1},v_{j_2},v_{j_3}
vj1,vj2,vj3,并连接每个
v
j
k
v_{j_k}
vjk到变量gadget中对应的字面量。(例如如果
l
i
1
=
x
i
l_{i_1}=x_i
li1=xi,将
v
j
1
v_{j_1}
vj1连接到
x
i
x_{i}
xi)
如下图所示。


因此现在对于每一个clause gadget triangle我们需要恰好选择两个顶点来覆盖该三角形的所有边。

但是我们对于升级的gadget里,如果变量gadget覆盖了否定。

有一种情况不行。
如果覆盖的是
x
i
x_i
xi。

只需要1+2三个节点就可以。
我们用直觉稍微解释一下。
图中的变量节点(如
x
i
x_i
xi和
x
i
‾
\overline{x_i}
xi)代表SAT问题中的变量及其否定形式。这些节点用于表示布尔变量的赋值。
对于每个子句(clause),根据SAT赋值选择两个节点。这些节点代表子句中的文字量(literals)。
如果一个字面量为真,其连接的子句节点不需要被选中。
如果一个字面量为假,其连接的子句节点必须被选中。
每个子句gadget必须至少有一个连接到一个真字面。(如上面的那种情况就不符合)
所以前面的式子所对应构造出来的图如下图所示。

根据我们现在前面的结论,对于每个变量,我们需要覆盖一个节点。对于每个子句我们需要覆盖两个节点。因此假设我们现在有
n
n
n个变量和
m
m
m个子句,那么现在需要选择的节点数
k
=
n
+
2
m
k=n+2m
k=n+2m,因此对于这个例子来说,
k
=
2
+
3
∗
2
=
8
k=2+3*2=8
k=2+3∗2=8。
现在我们开始说一下如何从3-SAT问题的解构造顶点覆盖问题的解:
变量选择(大小
n
n
n):如果
x
i
x_i
xi为真(true),则在顶点覆盖中选择
x
i
x_i
xi,否则选择
x
i
‾
\overline{x_i}
xi。这确保了变量节点之间的所有边都被覆盖。
子句选择(大小
2
m
2m
2m):对于每个子句
C
j
C_j
Cj,至少有一个字面
l
j
t
l_{j_t}
ljt为真(
t
=
[
1
,
2
,
3
]
t=[1,2,3]
t=[1,2,3])。选择与
l
j
t
l_{j_t}
ljt相连的两个顶点,以确保所有子句边都被覆盖。
总的顶点覆盖大小为
n
n
n(变量)加上
2
m
2m
2m(子句)。
所有的变都会被覆盖,VC也有会有正确的大小。
如下图所示。我们取
x
1
x_1
x1为假,
x
2
x_2
x2为真。

对于第一个子句,由于第三个字面也就是
l
1
3
l_{1_3}
l13为真,所以选择与其相连的两个顶点。
对于第二个子句,由于第一个字面也就是
l
2
1
l_{2_1}
l21为真,所以选择与其相连的两个顶点。
对于第三个子句,由于第二个字面也就是
l
1
3
l_{1_3}
l13为真,所以选择与其相连的两个顶点。
那么反过来如何从3SAT到VC呢?
给定条件:给定一个图
G
G
G有一个大小为
k
=
n
+
2
m
k=n+2m
k=n+2m的顶点覆盖
S
S
S,其中
n
n
n是变量的数量,
m
m
m是子句的数量。
变量赋值过程:
- 变量gadget处理:
对于每个变量gadget(每个变量及其否定形式对应的两个顶点),顶点覆盖集合 S S S中必须恰好有一个顶点被选中。
如果 x i x_i xi被选中(即 x i ∈ S x_i∈S xi∈S),则将∈S的值设为真(true)。
如果 x i ‾ \overline{x_i} xi被选中(即 x i ‾ ∈ S \overline{x_i}∈S xi∈S),则将∈S的值设为假(false)。 - 子句gadget处理:
对于每个子句gadget(每个子句对应的三角形),未选中的节点 v j t v_{j_t} vjt必须连接到 l j t l_{j_t} ljt的顶点gadget,而这个 l j t ( x i ) l_{j_t}(x_i) ljt(xi)的值为真,否则这条边 ( v j t , x i ) (v_{j_t},x_i) (vjt,xi)不会被覆盖。
因此对于每个子句,至少有一个字面为真,从而满足3-SAT公式 ϕ ϕ ϕ。
图的构造:
- 变量节点:
对于3-SAT问题中的每个变量 n n n,图中创建两个顶点,分别代表该变量及其否定形式。这会产生 2 n 2n 2n个顶点。
每个变量gadget(变量及其否定形式)之间有一条边相连,表示在顶点覆盖中,变量及其否定形式不能同时被选中。 - 子句节点:
对于3-SAT问题中的每个子句 m m m,图中创建一个包含三个顶点的三角形,代表子句中的三个字面量。这会产生 3 m 3m 3m个顶点。
每个子句gadget中的顶点连接到变量gadget中对应的字面,表示在顶点覆盖中,至少有一个字面需要被选中。一共为 3 m 3m 3m条边。
所以一共: - 顶点:
变量gadget产生的顶点: 2 n 2n 2n
子句gadget产生的顶点: 3 m 3m 3m
总顶点数量: 2 n + 3 m 2n+3m 2n+3m - 边:
变量gadget产生的边: n n n(每个变量gadget有一条边)
子句gadget内部的边: 3 m 3m 3m(每个子句gadget有三个顶点,形成三角形,有三条边)
子句gadget与变量gadget的连接边: 3 m 3m 3m(每个子句gadget的三个顶点分别连接到三个变量gadget)
总边数量: n + 3 m + 3 m = n + 6 m n+3m+3m=n+6m n+3m+3m=n+6m
因此算法复杂度为 O ( n + m ) O(n+m) O(n+m),所以从3-SAT问题构造VC问题的图的过程可以在多项式时间内完成,这意味着这种归约是有效的。
3. 优化问题(Optimization Problems)
说完决策问题,我们说优化问题。优化问题(Optimization problems)中我们的目标是最大化或最小化某个值。
即我们有一个问题实例
x
x
x,它有许多可行的“解决方案”。我们试图最小化(或最大化)某个成本函数
c
(
S
)
c(S)
c(S),其中
S
S
S是问题实例
x
x
x的一个“解决方案”。
例如:
- 最小生成树(Minimum Spanning Tree)
- 最小顶点覆盖(Smallest Vertex Cover)
系统一点的定义如下:
对于解决方法我们有一个可行解集(Feasible solution):对于每个问题实例
x
x
x,我们有一组可行解
F
(
x
)
F(x)
F(x)。这些解满足问题的所有约束条件。
成本函数(Cost function):每个可行解
s
∈
F
(
x
)
s∈F(x)
s∈F(x)都有一个成本
c
(
s
)
c(s)
c(s)。成本函数衡量解的优劣或效率。
最优成本(Optimum cost):最优成本
O
P
T
(
x
)
OPT(x)
OPT(x)定义为所有可行解中成本函数的最小值(或最大值,取决于是最小化还是最大化问题):
O
P
T
(
x
)
=
m
i
n
{
c
(
s
)
:
s
∈
F
(
x
)
}
OPT(x)=min\{c(s):s∈F(x)\}
OPT(x)=min{c(s):s∈F(x)}(或
m
a
x
max
max)。
许多计算问题都是NP完全优化问题。例如:寻找具有最小节点数的顶点覆盖。
3.1 近似比率(Approximation Ratio)
因此面对NP完全性问题我们要试着寻找尽可能好的解决方案。
那如何衡量解决方案的“好”呢?近似比率(approximation Ratio)是衡量解决方案质量的一个常用方法。
假设我们有一个算法,它为问题实例
x
x
x返回一个解决方案
T
(
x
)
T(x)
T(x)。
一种衡量解决方案质量的方法是比较算法找到的解决方案
T
(
x
)
T(x)
T(x) 的成本
c
(
T
(
x
)
)
c(T(x))
c(T(x))与最优解
O
P
T
(
x
)
OPT(x)
OPT(x)的成本
c
(
O
P
T
(
x
)
)
c(OPT(x))
c(OPT(x))的比率。
近似算法为优化问题产生一个解
T
T
T。
T
T
T是最优解
O
P
T
OPT
OPT的
k
k
k-近似,如果
c
(
T
)
/
c
(
O
P
T
)
≤
k
c(T)/c(OPT)≤k
c(T)/c(OPT)≤k(对于最小化问题)。
T
T
T是最优解
O
P
T
OPT
OPT的
k
k
k-近似,如果
c
(
O
P
T
)
/
c
(
T
)
≤
k
c(OPT)/c(T)≤k
c(OPT)/c(T)≤k(对于最大化问题)。
这里,
c
(
T
)
c(T)
c(T)是算法找到的解的成本,
c
(
O
P
T
)
c(OPT)
c(OPT)是最优解的成本。
k
k
k的值永远不会小于
1
1
1。
1
1
1-近似算法意味着找到的解就是最优解(
k
=
1
k=1
k=1,代表就是最优解)。
我们的目标是找到一个多项式时间的近似算法,具有较小的常数近似比率。
3.2 多项式时间近似方案(Polynomial-Time Approximation Schemes,简称PTAS)
近似方案是一种近似算法,它接受一个参数
ε
>
0
ε>0
ε>0作为输入,使得对于任何固定的
ε
>
0
ε>0
ε>0,该方案是一个
(
1
+
ε
)
(1+ε)
(1+ε)-近似算法。
这意味着算法找到的解的成本与最优解
O
P
T
OPT
OPT的成本之间的比率不超过
1
+
ε
1+ε
1+ε。
如果一个问题
L
L
L有一个多项式时间的
(
1
+
ε
)
(1+ε)
(1+ε)-近似算法,对于任何固定的
ε
>
0
ε>0
ε>0,那么
L
L
L有一个多项式时间近似方案(PTAS)。
这里的
(
1
+
ε
)
(1+ε)
(1+ε)-近似算法意味着算法找到的解的成本不超过最优解成本的
1
+
ε
1+ε
1+ε倍。
随着
ε
ε
ε的减小,算法的运行时间可能会迅速增加。这是因为更小的
ε
ε
ε值意味着需要更精确的解,这可能需要更多的计算资源。
例如,算法的运行时间可能是
O
(
n
2
/
ε
)
O(n^{2/ε})
O(n2/ε)
3.3 完全多项式时间近似方案(Fully Polynomial-Time Approximation Schemes,简称FPTAS)
当一个近似方案的运行时间是多项式,不仅与问题实例的大小
n
n
n成正比,而且与
1
/
ε
1/ε
1/ε也成正比时,我们称其为完全多项式时间近似方案(FPTAS)。
例如,算法的运行时间可能是
O
(
(
1
/
ε
)
3
n
2
)
O((1/ε)^3n^2)
O((1/ε)3n2)
3.4 顶点覆盖问题
我们现在再回到顶点覆盖问题。
顶点覆盖是顶点集 V 的一个子集
C
⊆
V
C⊆V
C⊆V,满足对于
E
E
E中的每条边
(
u
,
v
)
(u,v)
(u,v),至少有一个顶点
u
u
u或
v
v
v在
C
C
C中,或者两个顶点都在
C
C
C中。这意味着
C
C
C中的顶点“覆盖”了图中的每一条边。
所以现在关于顶点覆盖的优化问题OPT-VERTEX-COVER问题是给定一个图
G
G
G,找到
G
G
G的一个顶点覆盖,其大小尽可能小。
OPT-VERTEX-COVER问题是一个NP-hard问题。

3.4.1 关于顶点覆盖问题的近似算法
伪代码如下:

也就是在现在图中选择任意一条边,将这条边的两个端点
u
u
u和
v
v
v添加到顶点覆盖中。再移除所有与
u
u
u或
v
v
v相关的边(即所有以
u
u
u或
v
v
v为端点的边)。然后循环这个过程。
下面我们看一个例子,如图所示。

现在我们假设选择
{
b
,
c
}
\{b,c\}
{b,c},所以我们将这两个顶点添加到覆盖中,并将所有相邻的边去掉。

然后我们选择
{
e
,
f
}
\{e,f\}
{e,f},所以我们将这两个顶点添加到覆盖中,并将所有相邻的边去掉。

然后我们选择
{
d
,
g
}
\{d,g\}
{d,g},所以我们将这两个顶点添加到覆盖中,并将所有相邻的边去掉。

没有边剩余,所以这就是近似算法的结果。
下图的左边是我们得出的近似算法结果,右边是最优解结果。

这个算法是2-近似的,我们需要找到一个下界(lower bound)来估计最优解
C
∗
C^∗
C∗的大小。
证明如下:
A
A
A是算法第4行选择的边的集合。这些边是在算法的迭代过程中被选中的,用于构建顶点覆盖。
任何顶点覆盖必须覆盖集合
A
A
A中每条边至少一个端点。这是因为顶点覆盖的定义要求图中的每条边至少有一个端点在顶点覆盖中。
集合
A
A
A中的任意两条边不共享一个顶点。这是因为对于
A
A
A中的任意两条边,其中一条必须先被选中(第4行),然后在第6行中,所有与已选中边共享顶点的边将从边集
E
′
E'
E′中删除,因此它们在下一次迭代中不再被考虑。
为了覆盖集合
A
A
A,最优解
C
∗
C^*
C∗必须至少包含与
A
A
A中边数一样多的顶点。这是因为每条边至少需要一个顶点来覆盖,所以最优解的大小至少是
∣
A
∣
∣A∣
∣A∣。即
∣
A
∣
≤
∣
C
∗
∣
∣A∣ ≤ |C^*|
∣A∣≤∣C∗∣
算法的第4行选择一条边,这条边的两个端点都不在当前的顶点覆盖集合
C
C
C中。
第5行将这条边的两个端点添加到
C
C
C中。所以我们可以知道
∣
C
∣
=
2
∣
A
∣
∣C∣=2∣A∣
∣C∣=2∣A∣,其中
A
A
A是算法选择的所有边的集合。
因此
∣
C
∣
≤
2
∣
C
∗
∣
∣C∣ ≤ 2|C^*|
∣C∣≤2∣C∗∣。这意味着算法找到的顶点覆盖
C
C
C的大小不会超过最优解
C
∗
C^*
C∗的两倍。
由于
∣
C
∣
∣C∣
∣C∣不能大于最优解的两倍,所以这是一个顶点覆盖问题的
2
2
2-近似算法。
在近似算法的证明中,我们通常不知道最优解的大小,但我们可以通过设置一个下界来估计最优解的大小。
通过将找到的解与这个下界关联,我们可以证明算法的近似比率。
3.4.2 面对NP-hard优化问题的策略
我们可以使用以下策略:
- 使用已知的指数算法并限制在小规模问题上:
指数算法的运行时间随着输入大小呈指数增长,对于大规模问题来说非常慢。如果问题规模较小,可能还可以使用这类算法。 - 找出是否可以将问题限制到已知多项式时间解决方案的特殊情况:
有时可以通过限制问题到特定情况来简化问题,从而找到多项式时间的解决方案。
例如,顶点覆盖问题在二分图中可以在多项式时间内解决。 - 放弃最优解,寻找或设计一个提供“足够好”结果的近似算法:
近似算法旨在找到接近最优解的解,而不是最优解本身。
设计一个使用启发式(heuristic)的聪明近似算法。启发式是一种基于经验和直觉的解决问题的方法,它可能不保证找到最优解,但通常能找到足够好的解。(例如我们前面介绍的定点覆盖问题的近似解)
幸运地证明随机选择一个解已经足够好。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








