1. 随机游动模型
1.1 经过 n 步以后的位置特征
1.1.1 一维概率分布
若质点移动 n 步后到达η n= m 的位置,则所有的移动中,正方向移动
n
+
m
2
\frac{n + m}{2}
2n+m 步,反方向移动
n
−
m
2
\frac{n - m}{2}
2n−m步

这里的 是组合数C(n+m)/2n
是组合数C(n+m)/2n

1.1.2 例题
1.
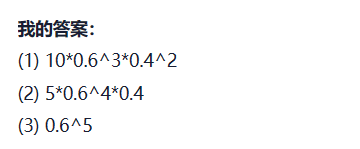
1.2 经过n步返回原点的概率


1.3 第一次返回原点的概率
第 2n 步第一次返回原点的概率记作:


2. 马尔可夫链
2.1 状态分析

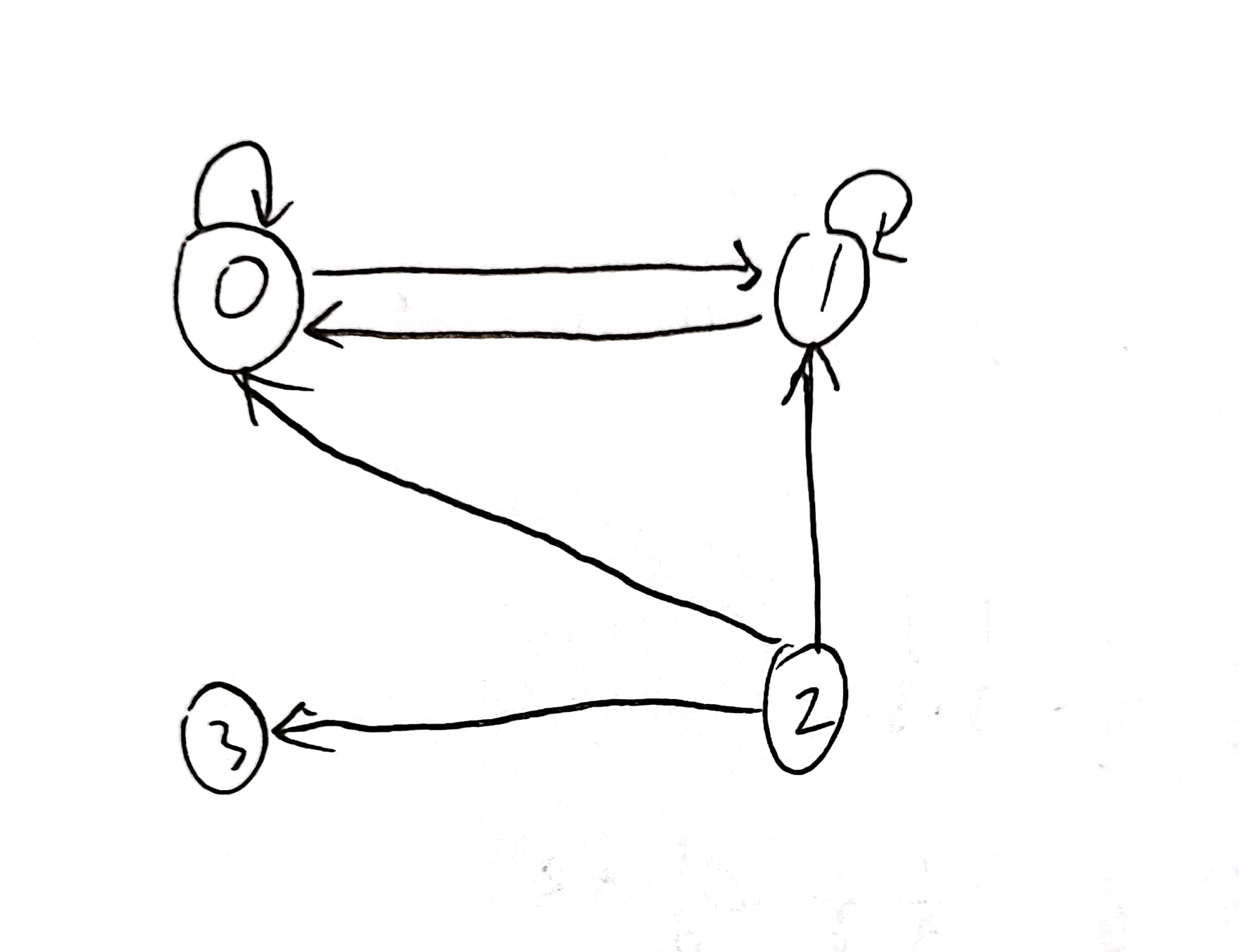
如图所示,状态2出发后不能返回自身,所以2是非常返态

2.2 例题
2.2.1 天气预报问题

2.2.2 带有两个吸收壁的随机游动

2.2.3 赌徒问题


3. 泊松过程

均值:E{N(t)}=λt
方差:D{N(t)}=λt
自相关函数:
自协方差函数:在这里插入图片描述
3.1 第一个事件到达时间的概率密度

3.2 第 n 个事件到达时间 t 的概率密度

3.3 非齐次泊松过程*

例题:
1.

2.

4. 马尔可夫过程
4.1 机器维修问题


4.2 排队问题
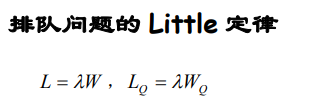
4.2.1 无限队长








4.2.2 有限队长


5. 非线性优化
5.1 凸函数

5.2 线搜索技术
5.2.1 0.618法

5.2.2 进退法

5.3 牛顿法
5.3.1 基本牛顿法

5.3.2 牛顿-最速下降混合算法

5.5 最小二乘法
二次多项式

5.6 KT条件求最优性条件

例题:
1.


5.7 罚函数
5.7.1 内点法


例题:
1.


5.7.2 外罚函数法

例题:
1.










 该文涵盖了随机游动模型的一维概率分布和返回原点概率,详细解释了马尔可夫链的状态分析和各类应用,包括天气预报和赌徒问题。此外,讨论了泊松过程的特性及非齐次泊松过程,并涉及非线性优化问题,如线搜索技术、牛顿法和罚函数法在解决凸函数和最优化问题中的应用。
该文涵盖了随机游动模型的一维概率分布和返回原点概率,详细解释了马尔可夫链的状态分析和各类应用,包括天气预报和赌徒问题。此外,讨论了泊松过程的特性及非齐次泊松过程,并涉及非线性优化问题,如线搜索技术、牛顿法和罚函数法在解决凸函数和最优化问题中的应用。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








