支持向量机学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。
对训练数据集找到间隔最大的超平面意味着以充分大的确信度对训练数据进行分类。
在这之前,需要先了解一下函数间隔和几何间隔的相关知识:
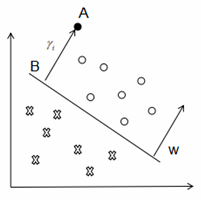
有A、B、C三个点,表示3个实例,均在分离超平面的正类的一侧,预测它们的类。
点A距分类超平面较远,若预测该点为正类,就比较确信预测是正确的;
点C距分类超平面较近,若预测该点为正类就不那么确信;
点B介于点A和C之间,预测其为正类的确信度也在A与C之间。
函数间隔:一个点距离分离超平面的远近可以表示分类预测的确信程度。
在超平面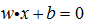
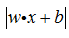
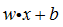
所以,可用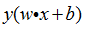
对于给定的训练数据集T和超平面
超平面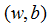
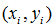
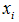
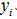
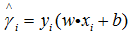
函数间隔最小值:
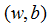
对超平面的法向量加某些约束,如规范化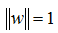
几何间隔:
当样本点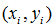
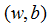
这也就是超平面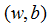
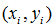
几何间隔最小值: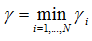
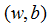
高亮!!!
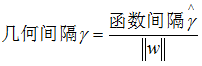
好啦,开头已经说啦,支持向量机学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。
so,问题变为,找到一个超平面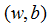
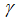
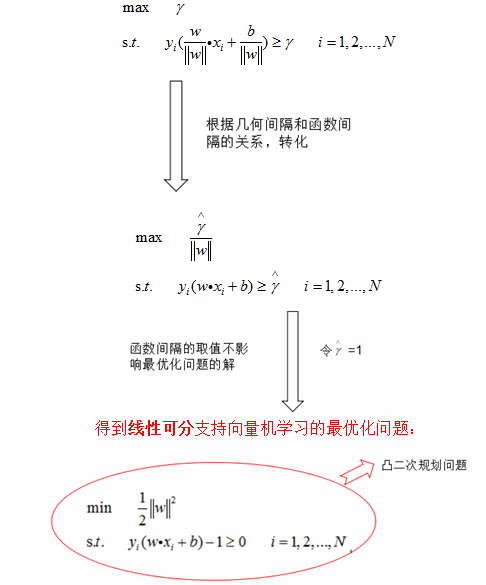
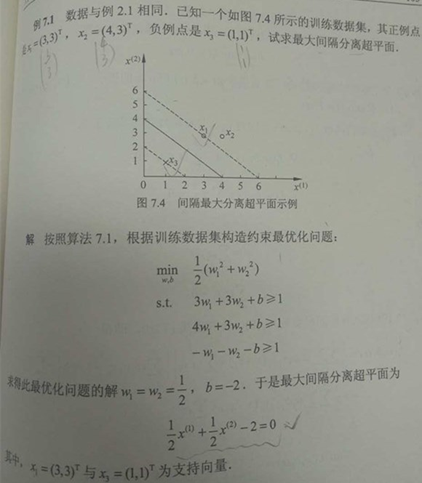
可以看出,在决定分离超平面时只有支持向量起作用!!其他实例点并不起作用(可以去掉),这种分类模型称为支持向量机。

下次,再继续学习线性不可分时的情况,啦啦啦,去吃饭啦~~
学习参考书籍:《统计学习方法》李航 著








 本文介绍了支持向量机(SVM)的学习基本思想,即寻找能够正确划分训练数据集且几何间隔最大的超平面。文中详细解释了函数间隔与几何间隔的概念,并通过实例直观展示了不同点与分类超平面之间的关系。
本文介绍了支持向量机(SVM)的学习基本思想,即寻找能够正确划分训练数据集且几何间隔最大的超平面。文中详细解释了函数间隔与几何间隔的概念,并通过实例直观展示了不同点与分类超平面之间的关系。

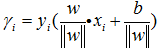
























 1774
1774

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








