欧氏距离:
欧几里得度量定义欧几里得空间中,点 x = (x1,...,xn) 和 y = (y1,...,yn) 之间的距离为
向量 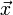 的自然长度,即该点到原点的距离为
的自然长度,即该点到原点的距离为
-
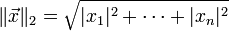 .
.
它是一个纯数值。在欧几里得度量下,两点之间直线最短。
马氏距离
马氏距离是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的,表示数据的协方差距离。它是一种有效的计算两个未知样本集 的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者 是有关联的)并且是尺度无关的(scale-invariant),即独立于测量尺度。 对于一个均值为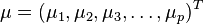 ,协方差矩阵为
,协方差矩阵为 的多变量向量
的多变量向量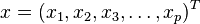 ,其马氏距离为
,其马氏距离为
马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为 的随机变量
的随机变量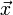 与
与 的差异程度:
的差异程度:
如果协方差矩阵为单位矩阵,马氏距离就简化为欧氏距离;如果协方差矩阵为对角阵,其也可称为正规化的欧氏距离。
其中 是
是 的标准差。
的标准差。
巴氏距离
在统计学中,巴氏距离(巴塔恰里雅距离 / Bhattacharyya distance)用于测量两离散概率分布。它常在分类中测量类之间的可分离性。在同一定义域X中,概率分布p和q的巴氏距离定义如下:其中(1)离散概率分布和(2)连续概率分布

BC是巴氏系数(Bhattacharyya coefficient)。
对于多维的正态分布


其中
具体可参见wikipedia上的信息
 and
and  分别是分布的期望与协方差矩阵
分别是分布的期望与协方差矩阵
,
-
 .
.




























 4438
4438

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








