[聚类一]之距离计算

距离计算

我们通常采用计算“距离”的方法来度量不同样本之间的相似性，进而判断该样本的大致类别。距离首先是一个几何概念，用$\mathrm{dist}(\cdot,\cdot)$表示，其中最为任熟悉的是二维和三维几何空间的欧几里德距离，随着数据维度的增大，距离在维数、幂次数等方面被推广了，距离被抽象为满足一些基本性质：

---

 非负性：

$$\mathrm{dist}(x_{i},x_{j})\geq0;\tag{1.1}$$
 同一性： $$\mathrm{dist}(x_{i},x_{j})=0，当且仅当x_{i}=x_{j};\tag{1.2}$$
 对称性： $$\mathrm{dist}(x_{i},x_{j})=\mathrm{dist}(x_{j},x_{i});\tag{1.3}$$
 直递性： $$\mathrm{dist}(x_{i},x_{j})\leq\mathrm{dist}(x_{i},x_{k})+\mathrm{dist}(x_{k},x_{j});\tag{1.3}$$
需要注意的是，用于相似度度量的距离未必一定满足以上所有的性质，尤其是直递性(1.3)。例如在某些任务中我们可能希望有这样的相似度度量：“人”“马”分别与“人马”相似，但“人”与“马”很不相似；要达到这个目的，可以令“人”“马”与“人马”之间的距离很小，但“人”与“马”之间的距离很大，如下图所示：

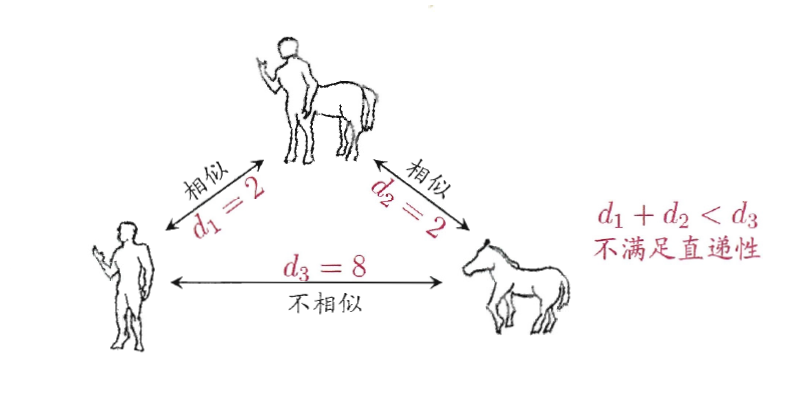
为了让大家对各种距离计算方法的应用场景有个清楚的认识，在讲距离计算方法之前，我先介绍一下几个名词。

• 属性：即样本本身所具有的特征，样本空间中的维度，就是属性的个数。
• 连续属性：样本的属性在定义域上有无穷多个可能的取值，比如说树的高度在$\left [ 7,10 \right ]$米之间，其取值是无穷多的。
• 离散属性：样本的属性在定义域上是有限个取值，比如说树的品种，肯定是有限的，只能从$\left \{ 白杨树,柳树,...,桃树\right \}$中取值，那么树的品种就属于离散属性
• 有序属性：就是说，属性的值能直接用来计算计算距离。例如树的高度。
• 无序属性：就是说，属性的值不能直接用来计算计算距离。例如树的品种。
  因此所有样本的属性都可划分为有序属性或者无序属性，或者同时具有有序属性和无序属性，这里我们成为混合属性。针对于有序属性的样本，我们常常使用闵科夫斯基距离计算公式来衡量样本之间的相似度，针对于无序属性的样本我们可采用$\mathrm{VDM}$ $( \mathrm{Value}$ Dif