前面的文章中我们讲过TPS变换的原理与实现,我们知道TPS变换模型既具有整体仿射变换特性,也具有一定的局部变换特性,因此可以使用该变换模型来做非刚性形变的配准:
同时我们前面也讲过梯度下降法优化算法的原理,以及基于FFD变换与梯度下降法的图像配准方法:
图像配准中,要对浮动图像进行tps变换,关键在于找到参考图像与浮动图像的多组匹配点对,然后将多组匹配点对输入tps变换模型,得到浮动图像到参考图像的坐标映射。前文中我们讲过使用特征点匹配的方法,以及使用光流跟踪的方法来寻找找到参考图像与浮动图像的匹配点对:
那么,能不能使用优化算法来寻找匹配点对呢?本人带着疑惑去尝试了一下,发现是可以的,本文我们主要讲的内容就是这个:一种基于tps变换与梯度下降法的配准方法。
1. 确定优化的目标函数及参数
前文我们讲基于FFD变换的配准方法时,有说过目标函数为:计算参考图像与经过FFD变换之后的浮动图像的互相关系数。基于tps变换与梯度下降法的配准方法也类似,也即计算参考图像与经过tps变换之后的浮动图像的互相关系数,如下图所示:

由上图可知,此时目标函数的输入参数由FFD控制参数变成了参考图像与浮动图像的匹配点对,变换模型由FFD变成了tps。
基于此方法,我们不必去找特征点并计算特征点的匹配,在配准开始之前,我们只需要在参考图像与浮动图像上面初始化一系列等间距的点,并假设两图中相同位置的点为匹配点对,然后在此基础上使用梯度下降法一步一步优化浮动图像上初始点的位置,使得浮动图像与参考图像上的点达到真正的匹配。如下图所示:

在这里需要强调的是,我们并不需要优化参考图像上点的位置,我们只需要固定参考图像上点的位置,然后优化浮动图像上点的位置,使其与参考图像上点的位置匹配即可。所以,上面我们说目标函数的输入参数是参考图像与浮动图像的匹配点对,其实需要优化的只有浮动图像上点的位置。假设参考图像与浮动图像上初始化的等间距的点个数都是N个,每个点包含x坐标和y坐标,那么我们需要优化的参数为浮动图像上所有初始化点的x、y坐标组成的2*N个参数。
2. 代码实现
(1) tps变换代码
由于tps变换的计算量很大,此处我们使用CUDA对其并行加速,避免配准速度慢得离谱~
前文我们讲tps的计算原理时有说过(参考本文开头的链接),计算每个点的坐标映射,包含了大量的计算:
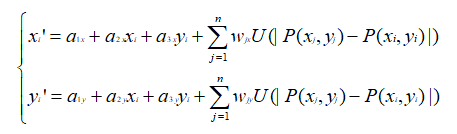
所以我们的并行加速思路可以从此处着手,假设图像大小为m行n列,那么我们可以开启m*n个线程来并行计算每个点的坐标映射,可大大减少计算耗时。
首先,在CPU端计算W矩阵:
//TPS基函数,r为两点距离的平方
double tps_basis(double r)
{
if(r == 0.0)
{
return 0.0;
}
else
{
return (r*log(r));
}
}
//计算K矩阵
void cal_K(vector<Point2f> P, Mat &K)
{
if(K.empty())
{
K.create(P.size(), P.size(), CV_32FC1);
}
else if(K.rows != P.size() || K.cols != P.size())
{
resize(K, K, Size(P.size(), P.size()));
}
for(int i = 0; i < P.size(); i++)
{
for(int j = i; j < P.size(); j++)
{
Point2f diff_p = P[i] - P[j];
double diff = diff_p.x*diff_p.x + diff_p.y*diff_p.y;
float U = (float)tps_basis(diff);
K.ptr<float>(i)[j] = U;
K.ptr<float>(j)[i] = U;
}
}
}
//计算L矩阵
void cal_L(vector<Point2f> points1, Mat &L)
{
int N = points1.size();
Mat L_tmp = Mat::zeros(Size(N+3, N+3), CV_32FC1);
Mat P = Mat::ones(Size(3, N), CV_32FC1);
for(int i = 0; i < N; i++)
{
P.ptr<float>(i)[1] = points1[i].x;
P.ptr<float>(i)[2] = points1[i].y;
}
Mat P_T;
transpose(P, P_T);
Mat K;
cal_K(points1, K);
K.copyTo(L_tmp(Rect(0, 0, N, N)));
P.copyTo(L_tmp(Rect(N, 0, 3, N)));
P_T.copyTo(L_tmp(Rect(0, N, N, 3)));
L = L_tmp.clone();
}
//计算W矩阵
void cal_W(vector<Point2f> points1, vector<Point2f> points2, Mat &W)
{
int N = points1.size();
Mat L;
cal_L(points1, L);
Mat Y = Mat::zeros(Size(2, N+3), CV_32FC1); //row:N+3, col:2
for(int i = 0; i < N; i++)
{
Y.ptr<float>(i)[0] = points2[i].x;
Y.ptr<float>(i)[1] = points2[i].y;
}
solve(L, Y, W, DECOMP_EIG);
}
其次,在GPU端并行计算每个点的坐标映射:
//核函数,计算坐标变换,并使用最邻近插值算法或者双线性插值算法进行像素重采样
__global__ void Tps_warpImage_kernel(uchar *transformingImage, uchar *output, float *points1, float *W, int row, int col, int N, int inner_type, float *Tx, float *Ty)
{
int j = threadIdx.x + blockDim.x * blockIdx.x; //col
int i = threadIdx.y + blockDim.y * blockIdx.y; //row
if(i < row && j < col)
{
float x = float(j);
float y = float(i);
float nonrigid_x = 0;
float nonrigid_y = 0;
for (int j = 0; j < N; j++)
{
float diff_x = points1[j] - x;
float diff_y = points1[j + N] - y;
double diff = (diff_x*diff_x + diff_y*diff_y);
if (diff > 0.0000001)
{
double tps_diff = diff*log(diff);
nonrigid_x += W[j * 2] * tps_diff;
nonrigid_y += W[j * 2 + 1] * tps_diff;
}
}
x = W[N * 2] + W[(N + 1) * 2] * x + W[(N + 2) * 2] * y + nonrigid_x;
y = W[N * 2 + 1] + W[(N + 1) * 2 + 1] * x + W[(N + 2) * 2 + 1] * y + nonrigid_y;
int x1 = floor(x);
int y1 = floor(y);
Tx[i*col + j] = x;
Ty[i*col + j] = y;
if (y1<0 || y1>=row || x1<0 || x1>=col)//越界
{
output[i*col+j] = 0;
}
else
{
if(inner_type == 0) //最邻近插值
{
int xx = (int)(x+0.5); //四舍五入
int yy = (int)(y+0.5);
output[i*col+j] = transformingImage[yy*col+xx];
}
else if(inner_type == 1) //双线性插值
{
int x2 = x1 + 1;
int y2 = y1 + 1;
uchar pointa = transformingImage[y1*col+x1];
uchar pointb = transformingImage[y1*col+x2];
uchar pointc = transformingImage[y2*col+x1];
uchar pointd = transformingImage[y2*col+x2];
uchar gray = (uchar)((x2 - x)*(y2 - y)*pointa - (x1 - x)*(y2 - y)*pointb - (x2 - x)*(y1 - y)*pointc + (x1 - x)*(y1 - y)*pointd);
output[i*col+j] = gray;
}
}
__syncthreads();
}
}
//主体函数
void Tps_warpImage_cuda(Mat transformingImage, Mat &output, Mat &Tx, Mat &Ty, vector<Point2f> points1, vector<Point2f> points2, int inner_type)
{
int N = points1.size();
int point_size = 2*N*sizeof(float);
int img_size = transformingImage.rows*transformingImage.cols;
uchar *transformingImage_cuda;
uchar *output_cuda;
float *points1_cuda;
float *Tx_cuda;
float *Ty_cuda;
float *points1_host = (float *)malloc(point_size);
uchar *output_host = (uchar *)malloc(img_size);
float *Tx_host = (float *)malloc(img_size*sizeof(float));
float *Ty_host = (float *)malloc(img_size*sizeof(float));
cudaMalloc((void**)&transformingImage_cuda, img_size);
cudaMalloc((void**)&output_cuda, img_size);
cudaMalloc((void**)&points1_cuda, point_size);
cudaMalloc((void**)&Tx_cuda, img_size*sizeof(float));
cudaMalloc((void**)&Ty_cuda, img_size*sizeof(float));
for(int i = 0; i < N; i++)
{
points1_host[i] = points1[i].x;
points1_host[i+N] = points1[i].y;
}
cudaMemcpy(points1_cuda, points1_host, point_size, cudaMemcpyHostToDevice);
cudaMemcpy(transformingImage_cuda, transformingImage.data, img_size, cudaMemcpyHostToDevice);
dim3 Block_tps(16, 16);
dim3 Grid_tps((transformingImage.cols+15)/16, (transformingImage.rows+15)/16);
Mat W;
cal_W(points1, points2, W); //cpu端计算得到矩阵W之后,再在GPU端并行计算坐标映射
float *W_cuda;
cudaMalloc((void**)&W_cuda, 2*(N+3)*sizeof(float));
cudaMemcpy(W_cuda, (float *)W.data, 2*(N+3)*sizeof(float), cudaMemcpyHostToDevice);
Tps_warpImage_kernel<<<Grid_tps, Block_tps>>>(transformingImage_cuda, output_cuda, points1_cuda, W_cuda, transformingImage.rows, transformingImage.cols, N, inner_type, Tx_cuda, Ty_cuda);
cudaMemcpy(output_host, output_cuda, img_size, cudaMemcpyDeviceToHost);
cudaMemcpy(Tx_host, Tx_cuda, img_size*sizeof(float), cudaMemcpyDeviceToHost);
cudaMemcpy(Ty_host, Ty_cuda, img_size*sizeof(float), cudaMemcpyDeviceToHost);
Mat tmp(Size(transformingImage.cols, transformingImage.rows), CV_8UC1, output_host);
Mat Tx_tmp(Size(transformingImage.cols, transformingImage.rows), CV_32FC1, Tx_host);
Mat Ty_tmp(Size(transformingImage.cols, transformingImage.rows), CV_32FC1, Ty_host);
tmp.copyTo(output);
Tx_tmp.copyTo(Tx);
Ty_tmp.copyTo(Ty);
cudaFree(transformingImage_cuda);
cudaFree(output_cuda);
cudaFree(points1_cuda);
cudaFree(W_cuda);
cudaFree(Tx_cuda);
cudaFree(Ty_cuda);
free(points1_host);
free(output_host);
free(Tx_host);
free(Ty_host);
}
(2) 分块计算两张图像互相关系数的代码
//函数返回值越小说明S1、Si越相似
//row表示行向分块数
//col表示列向分块数
double cal_cc_block(Mat S1, Mat Si, int row, int col)
{
int ksize_row = S1.rows / row;
int ksize_col = S1.cols / col;
Mat tmp1, tmpi;
double sum = 0.0;
for (int i = 0; i < row; i++)
{
int i_begin = i*ksize_row;
for (int j = 0; j < col; j++)
{
double sum1 = 0.0;
double sum2 = 0.0;
double sum3 = 0.0;
int j_begin = j*ksize_col;
for (int t1 = i_begin; t1 < i_begin + ksize_row; t1++)
{
uchar *S1_data = S1.ptr<uchar>(t1);
uchar *Si_data = Si.ptr<uchar>(t1);
for (int t2 = j_begin; t2 < j_begin + ksize_col; t2++)
{
sum1 += S1_data[t2] * Si_data[t2];
sum2 += S1_data[t2] * S1_data[t2];
sum3 += Si_data[t2] * Si_data[t2];
}
}
sum += sqrt(sum2*sum3) / (sum1 + 0.0000001);
}
}
sum /= (row*col);
return sum;
}
(3) 目标函数的代码
float F_fun_tps(Mat S1, Mat Si, vector<Point2f> p1, vector<Point2f> p2)
{
double result;
Mat Si_tmp;
Mat Tx, Ty;
Tps_warpImage_cuda(Si, Si_tmp, Tx, Ty, p1, p2, 1);
result = cal_cc_block(S1, Si_tmp, 3, 3); //默认分为3*3块计算互相关
return result;
}
(4) 计算梯度的代码
//EPS取一个较小的值,比如0.1、0.5、1.0
//p1,参考图像上的点,不需要优化(是固定不变的),因此不需要计算梯度
/p2,浮动图像上的点,x、y坐标需要优化,需要计算梯度
void cal_gradient_tps(Mat S1, Mat Si, vector<Point2f> p1, vector<Point2f> p2, Mat &gradient, float EPS=0.5)
{
gradient.create(2, p2.size(), CV_32FC1);
float a1 = F_fun_tps(S1, Si, p1, p2);
vector<Point2f> p = p2;
int cnt = 0;
for (int i = 0; i < p2.size(); i++)
{
//计算x坐标梯度
p[i].x += EPS;
float a2 = F_fun_tps(S1, Si, p1, p);
p[i].x -= EPS;
gradient.at<float>(0, i) = (a2 - a1) / EPS;
//计算y坐标梯度
p[i].y += EPS;
a2 = F_fun_tps(S1, Si, p1, p);
p[i].y -= EPS;
gradient.at<float>(1, i) = (a2 - a1) / EPS;
}
}
(5) 更新参数的代码
void update_grid_points_tps(vector<Point2f> &p2, Mat gradient, float alpha)
{
for (int i = 0; i < p2.size(); i++)
{
//更新x坐标
p2[i].x = p2[i].x - gradient.at<float>(0, i)*alpha;
//更新y坐标
p2[i].y = p2[i].y - gradient.at<float>(1, i)*alpha;
}
}
(6) 主体配准代码
int tps_match(Mat S1, Mat Si, Mat &M, vector<Point2f> p1, vector<Point2f> &p2)
{
int max_iter = 5000; //最多迭代次数
Mat gradient;
Mat pre_gradient = Mat::zeros(2, p2.size(), CV_32FC1);
vector<Point2f> pre_p2;
double e = 0.000005; //定义迭代精度
float ret1 = 0.0;
float ret2 = 0.0;
int cnt = 0;
float alpha = 8000000;
float EPS = 0.1;
cal_gradient_tps(S1, Si, p1, p2, gradient, EPS); //求梯度
int out_cnt = 0;
while (cnt < max_iter)
{
pre_p2 = p2;
update_grid_points_tps(p2, gradient, alpha); //更新输入参数
ret1 = F_fun_tps(S1, Si, p1, pre_p2);
ret2 = F_fun_tps(S1, Si, p1, p2);
if (ret2 > ret1) //如果当前轮迭代的目标函数值大于上一轮的函数值,则减小步长并重新计算梯度、重新更新参数
{
alpha *= 0.5;
p2 = pre_p2;
continue;
}
cout << "f=" << ret2 << ", alpha=" << alpha << ", EPS=" << EPS <<endl;
if (abs(ret2 - ret1) < e)
{
out_cnt++;
if (out_cnt >= 4) //如果连续4次目标函数值不改变,则认为求到了最优解,停止迭代
{
Mat Tx, Ty;
Tps_warpImage_cuda(Si, M, Tx, Ty, p1, p2, 1);
update_flag = Mat::zeros(1, p1.size(), CV_8UC1); //初始化标记为0
return 0;
}
}
else
{
out_cnt = 0;
}
gradient.copyTo(pre_gradient);
cal_gradient_tps(S1, Si, p1, p2, gradient, EPS); //求梯度
if (norm(gradient, NORM_L2) <= norm(pre_gradient, NORM_L2)) //如果梯度相比上一次迭代有所下降,则增大步长
{
alpha *= 3.0;
}
cnt++;
}
return -1;
}
(7) 初始化等间距点的代码
void init_points(Mat src, int row_block_num, int col_block_num, vector<Point2f> &p1, vector<Point2f> &p2)
{
float row_block_size = src.rows * 1.0 / (row_block_num-1);
float col_block_size = src.cols * 1.0 / (col_block_num-1);
p1.clear();
p2.clear();
for (int i = 0; i < row_block_num; i++)
{
for (int j = 0; j < col_block_num; j++)
{
float x = j*col_block_size;
float y = i*row_block_size;
x = x > src.cols - 1 ? src.cols - 1 : x; //超出范围处理
y = y > src.rows - 1 ? src.rows - 1 : y; //超出范围处理
Point2f p(x, y);
p1.push_back(p);
p2.push_back(p);
}
}
}
(8) 测试代码
使用以上实现的配准方法,对脑部图像进行配准。
void tps_gradient_test(void)
{
Mat img1 = imread("brain3.png", CV_LOAD_IMAGE_GRAYSCALE);
Mat img2 = imread("brain4.png", CV_LOAD_IMAGE_GRAYSCALE);
imshow("image before", img1);
imshow("image2 before", img2);
vector<Point2f> p1, p2;
int row_block_num = 10;
int col_block_num = 10;
init_points(img1, row_block_num, col_block_num, p1, p2); //在参考图像与浮动图像上分别初始化等间距点
Mat out;
tps_match(img1, img2, out, p1, p2); //配准
//画出优化前后的点位置
Mat img1_grid = img1.clone();
Mat img2_grid = img2.clone();
Mat img3_grid = img2.clone();
cvtColor(img1_grid, img1_grid, CV_GRAY2BGR);
cvtColor(img2_grid, img2_grid, CV_GRAY2BGR);
cvtColor(img3_grid, img3_grid, CV_GRAY2BGR);
for (int i = 0; i < row_block_num; i++)
{
for (int j = 0; j < col_block_num; j++)
{
int idx = i*col_block_num + j;
circle(img1_grid, p1[idx], 2, Scalar(0, 0, 255), 2);
circle(img2_grid, p2[idx], 2, Scalar(0, 0, 255), 2);
circle(img3_grid, p1[idx], 2, Scalar(0, 0, 255), 2);
if (i > 0 && j > 0)
{
line(img1_grid, p1[idx], p1[i*(col_block_num)+j-1], Scalar(255, 0, 0), 1);
line(img1_grid, p1[idx], p1[(i-1)*(col_block_num)+j], Scalar(255, 0, 0), 1);
line(img2_grid, p2[idx], p2[i*(col_block_num)+j-1], Scalar(255, 0, 0), 1);
line(img2_grid, p2[idx], p2[(i-1)*(col_block_num)+j], Scalar(255, 0, 0), 1);
line(img3_grid, p1[idx], p1[i*(col_block_num)+j - 1], Scalar(255, 0, 0), 1);
line(img3_grid, p1[idx], p1[(i - 1)*(col_block_num)+j], Scalar(255, 0, 0), 1);
}
}
}
imshow("img1_grid", img1_grid);
imshow("img2_grid", img2_grid);
imshow("img3_grid", img3_grid);
imshow("img2-img1", abs(img2 - img1));
imshow("tps_out-img1", abs(out - img1));
imshow("tps_out", out);
waitKey();
}
3. 测试结果

参考图像

浮动图像
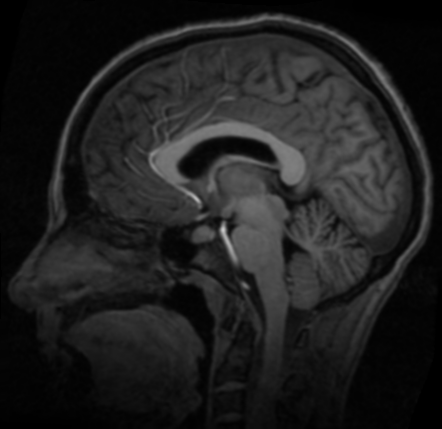
配准图像

参考图像与浮动图像的差值图

参考图像与配准图像的差值图

配准前后初始化点的位置
4. tps+梯度下降配准方法的改进
(1) 部分点更新策略
在配准开始之前,我们在参考图像与浮动图像上分别初始化了一系列等间隔的点,然后对浮动图像上点的坐标位置进行梯度下降优化,使其与参考图像的点匹配,这个过程中我们需要优化的是浮动图像上初始化的点,每次更新参数之前,都需要计算浮动图像上所有初始化点的x、y坐标的梯度。
我们考虑到以下两种情况,浮动图像上部分点本来就不需要优化,或者在某一轮迭代之后不再需要继续优化了:
a. 往往浮动图像相对于参考图像的形变并不是全部区域的形变,很有可能部分区域本来就是位置对齐的,浮动图像上面位于这些区域的初始点本来就与参考图像的对应初始点匹配了,因此不再需要对其优化。
b. 在优化过程中,浮动图像上部分点的坐标位置经过优化之后已经与参考图像的点达成匹配,不再需要继续优化。
基于上述原因,为了减少配准耗时,并使配准更稳定,我们可以实现一个部分点优化策略:每轮迭代时,通过判断某一点x、y坐标的梯度是否都小于一定数值,如果是则认为该点的坐标位置不再需要优化,在接下来的迭代中不再对其x、y坐标进行更新。
(2) 梯度继承策略
当前轮的迭代是在上一轮迭代的基础上进行的,因此相邻轮迭代的梯度具有一定的继承关系,我们可以将上一轮迭代的梯度以一定比例叠加到当前轮的梯度,这样可以增加收敛速度:
cur_gradient = cur_gradient + α*pre_gradient
α通常取一个较小的数值,比如0.1~0.25之间的一个固定数值。
改进之后的代码大同小异:
//定义一个全局标记,标记浮动图像上的初始点是否需要更新
Mat update_flag;
void cal_gradient_tps(Mat S1, Mat Si, vector<Point2f> p1, vector<Point2f> p2, Mat &gradient, float EPS=0.5)
{
gradient.create(2, p2.size(), CV_32FC1);
float a1 = F_fun_tps(S1, Si, p1, p2);
uchar *flag_p = update_flag.ptr<uchar>(0);
vector<Point2f> p = p2;
int cnt = 0;
for (int i = 0; i < p2.size(); i++)
{
if (!flag_p[i]) //如果标记为0表示需要更新
{
p[i].x += EPS;
float a2 = F_fun_tps(S1, Si, p1, p);
p[i].x -= EPS;
gradient.at<float>(0, i) = (a2 - a1) / EPS;
p[i].y += EPS;
a2 = F_fun_tps(S1, Si, p1, p);
p[i].y -= EPS;
gradient.at<float>(1, i) = (a2 - a1) / EPS;
//判断x、y坐标的梯度是否都小于0.000001,如果都小于则对标志置1,表示该点不再需要更新
if (abs(gradient.at<float>(0, i)) < 1e-6 && abs(gradient.at<float>(1, i)) < 1e-6)
{
flag_p[i] = 1;
}
cnt++;
}
else
{
gradient.at<float>(0, i) = 0;
gradient.at<float>(1, i) = 0;
}
}
printf("update points num: %d\n", cnt);
}
void update_grid_points_tps(vector<Point2f> &p2, Mat gradient, float alpha)
{
uchar *flag_p = update_flag.ptr<uchar>(0);
for (int i = 0; i < p2.size(); i++)
{
if (!flag_p[i]) //如果标记为0表示需要更新,否则不更新
{
p2[i].x = p2[i].x - gradient.at<float>(0, i)*alpha;
p2[i].y = p2[i].y - gradient.at<float>(1, i)*alpha;
}
}
}
int tps_match(Mat S1, Mat Si, Mat &M, vector<Point2f> p1, vector<Point2f> &p2)
{
update_flag = Mat::zeros(1, p1.size(), CV_8UC1); //初始化标记为0
int max_iter = 5000; //最多迭代次数
Mat gradient;
Mat pre_gradient = Mat::zeros(2, p2.size(), CV_32FC1);
vector<Point2f> pre_p2;
double e = 0.000005;//定义迭代精度
float ret1 = 0.0;
float ret2 = 0.0;
int cnt = 0;
float alpha = 8000000;
float EPS = 0.1;
cal_gradient_tps(S1, Si, p1, p2, gradient, EPS); //求梯度
int out_cnt = 0;
vector<double> time;
vector<double> ff;
Timer_Us timer;
double tt = 0;
while (cnt < max_iter)
{
pre_p2 = p2;
gradient = gradient + pre_gradient*0.1; //将上一轮的梯度乘以0.1累加到当前轮的梯度
update_grid_points_tps(p2, gradient, alpha); //更新输入参数
ret1 = F_fun_tps(S1, Si, p1, pre_p2);
ret2 = F_fun_tps(S1, Si, p1, p2);
if (ret2 > ret1) //如果当前轮迭代的目标函数值大于上一轮的函数值,则减小步长并重新计算梯度、重新更新参数
{
alpha *= 0.5;
p2 = pre_p2;
continue;
}
cout << "f=" << ret2 << ", alpha=" << alpha << ", EPS=" << EPS <<endl;
if (abs(ret2 - ret1) < e)
{
out_cnt++;
if (out_cnt >= 4) //如果连续4次目标函数值不改变,则认为求到了最优解,停止迭代
{
//Bspline_Ffd_cuda(Si, M, row_block_num, col_block_num, grid_points);
Mat Tx, Ty;
//Tps_TxTy_cuda(p1, p2, S1.rows, S1.cols, Tx, Ty);
//remap(Si, M, Tx, Ty, INTER_CUBIC);
Tps_warpImage_cuda(Si, M, Tx, Ty, p1, p2, 1);
update_flag = Mat::zeros(1, p1.size(), CV_8UC1); //初始化标记为0
return 0;
}
}
else
{
out_cnt = 0;
}
gradient.copyTo(pre_gradient);
cal_gradient_tps(S1, Si, p1, p2, gradient, EPS); //求梯度
if (norm(gradient, NORM_L2) <= norm(pre_gradient, NORM_L2)) //如果梯度相比上一次迭代有所下降,则增大步长
{
alpha *= 3.0;
}
cnt++;
}
update_flag = Mat::zeros(1, p1.size(), CV_8UC1); //初始化标记为0
return -1;
}
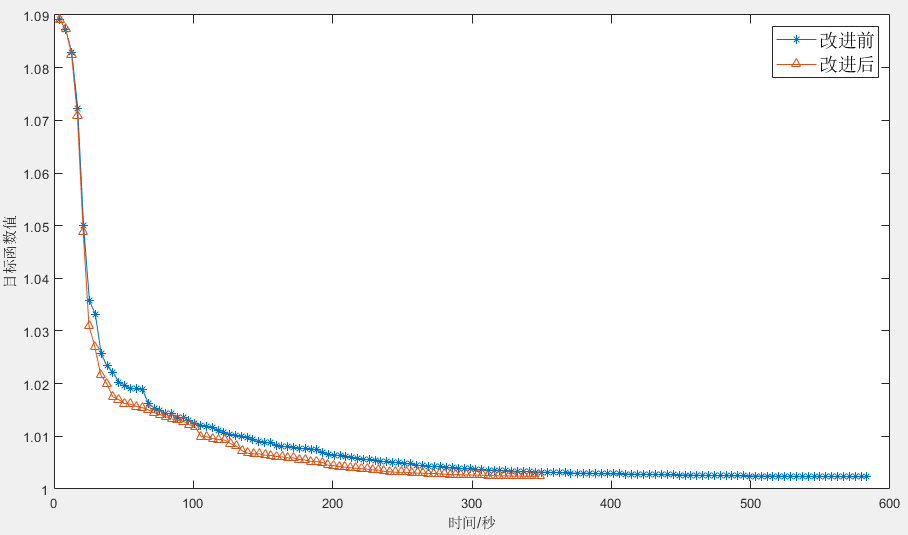
运行改进后的配准方法代码,对同样的脑部图像进行配准,并于改进前的方法进行比较,如下图所示,可以看到改进后配准的收敛速度快了不少。
本文提出这种配准方法,目的只是抛砖引玉,也许相对于基于特征点匹配的配准方法,优势并没有明显多少,但如果能给大家带来新的启发,我就很开心啦~
欢迎扫码关注以下微信公众号,接下来会不定时更新更加精彩的内容噢~


























 2433
2433

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










