9.5.2 椭圆模型拟合及案例
多元数据集存在偏离正常范围的“离群点”。一般在预处理数据环节,需检测出离群点,再进行处理。
离群点产生的原因可能是由数据中存在某些点来自于与总体分布不同的其它分布。具体而言,假设多元数据集大多数样本服从分布F,少量样本服从分布G;则将少量样本定义为离群点。
一般采用马氏距离来检验某个样本是否为离群点。在计算距离过程中需要提供均值估计量和协方差估计量,这两个参数容易被离群值影响而发生偏离,导致马氏距离计算不准确,最终影响离散点的判断。
实现离群点检测的一种常见方式是假设常规数据来自已知分布(例如,数据服从高斯分布)。 从这个假设来看,我们通常试图定义数据的“形状”,并且可以将偏远观测(outlying observation)定义为足够远离拟合形状的观测。

scikit-learn 提供了covariance.EllipticEnvelope对象,它能拟合出数据的稳健协方差估计,从而为中心数据点拟合出一个椭圆,忽略不和该中心模式相关的点。
例如,假设数据服从高斯分布,它将稳健地(即不受异常值的影响)估计位置和协方差。从而估计得到的马氏距离用于得出偏远性度量。
由于直接计算均值和协方差两个估计量易受离群值影响而发生偏移,马氏距离计算不准确,进而对离群值的判断出现失误。为了获取更加稳健的估计量,最小协方差行列式(MCD)被提出,提高了离群点探测的准确度。利用最小协方差行列式计算可以获取更稳健的均值和协方差估计量,再根据马氏距离计算,可以更精准地探测离群点。他的基本原理是找到样本量为s的子集,使得在所有大小为s的子集中,该子集的协方差矩阵的行列式是最小的。
下面的案例说明对位置和协方差使用标准估计或稳健估计来评估观测值的偏远性的差异,代码如下:
#导入相关库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.covariance import EmpiricalCovariance, MinCovDet
#正常显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
n_samples = 150
n_outliers = 50
n_features = 2
#生成数据
gen_cov = np.eye(n_features)
gen_cov[0, 0] = 2.
X = np.dot(np.random.randn(n_samples, n_features), gen_cov)
#添加一些离群值
outliers_cov = np.eye(n_features)
outliers_cov[np.arange(1, n_features), np.arange(1, n_features)] = 7.
X[-n_outliers:] = np.dot(np.random.randn(n_outliers, n_features), outliers_cov)
#稳健估计拟合数据
robust_cov = MinCovDet().fit(X)
#估计量与真实参数比较
emp_cov = EmpiricalCovariance().fit(X)
#显示结果
fig = plt.figure(figsize= (11, 8))
plt.subplots_adjust(hspace=-.15, wspace=.6, top=.95, bottom=.05)
#显示数据集
subfig1 = plt.subplot(3, 1, 1)
inlier_plot = subfig1.scatter(X[:, 0], X[:, 1],color='black', label='正常值')
outlier_plot = subfig1.scatter(X[:, 0][-n_outliers:], X[:, 1][-n_outliers:],color='red', label='离群点')
subfig1.set_xlim(subfig1.get_xlim()[0], 11.)
subfig1.set_title("数据集的马氏距离", fontsize=16)

#显示距离函数的轮廓
xx, yy = np.meshgrid(np.linspace(plt.xlim()[0], plt.xlim()[1], 100),
np.linspace(plt.ylim()[0], plt.ylim()[1], 100))
zz = np.c_[xx.ravel(), yy.ravel()]
#极大似然估计
mahal_emp_cov = emp_cov.mahalanobis(zz)
mahal_emp_cov = mahal_emp_cov.reshape(xx.shape)
emp_cov_contour = subfig1.contour(xx, yy, np.sqrt(mahal_emp_cov),
cmap=plt.cm.PuBu_r,linestyles='dashed')
#最小协方差行列式
mahal_robust_cov = robust_cov.mahalanobis(zz)
mahal_robust_cov = mahal_robust_cov.reshape(xx.shape)
robust_contour = subfig1.contour(xx, yy, np.sqrt(mahal_robust_cov),
cmap=plt.cm.YlOrBr_r, linestyles='dotted')
subfig1.legend([emp_cov_contour.collections[1], robust_contour.collections[1],inlier_plot, outlier_plot],['极大似然估计距离', '最小协方差行列式距离', '正常值', '离群点'],loc="upper right", borderaxespad=0, fontsize=15)
plt.xticks(())
plt.yticks(())
#绘制每个点的分数
emp_mahal = emp_cov.mahalanobis(X - np.mean(X, 0)) ** (0.5)
subfig2 = plt.subplot(2, 2, 3)
subfig2.boxplot([emp_mahal[:-n_outliers], emp_mahal[-n_outliers:]], widths=.15)
subfig2.plot(np.full(n_samples - n_outliers, 1.26),
emp_mahal[:-n_outliers], '+k', markeredgewidth=1)
subfig2.plot(np.full(n_outliers, 2.26),
emp_mahal[-n_outliers:], '+k', markeredgewidth=1)
subfig2.axes.set_xticklabels(('正常值', '离群点'), size=15)
subfig2.set_ylabel(r"马氏距离的平方根", size=15)
subfig2.set_title("1.不稳健估计\n(极大似然估计)", fontsize=16)
plt.yticks(())
robust_mahal = robust_cov.mahalanobis(X - robust_cov.location_) ** (0.5)
subfig3 = plt.subplot(2, 2, 4)
subfig3.boxplot([robust_mahal[:-n_outliers], robust_mahal[-n_outliers:]],widths=.25)
subfig3.plot(np.full(n_samples - n_outliers, 1.26),
robust_mahal[:-n_outliers], '+k', markeredgewidth=1)
subfig3.plot(np.full(n_outliers, 2.26),
robust_mahal[-n_outliers:], '+k', markeredgewidth=1)
subfig3.axes.set_xticklabels(('正常值', '离群点'), size=15)
subfig3.set_ylabel(r"马氏距离的平方根", size=15)
subfig3.set_title("2.稳健估计\n(最小协方差行列式)", fontsize=16)
plt.yticks(())
plt.show()
运行上述代码,输出如图9-14所示。
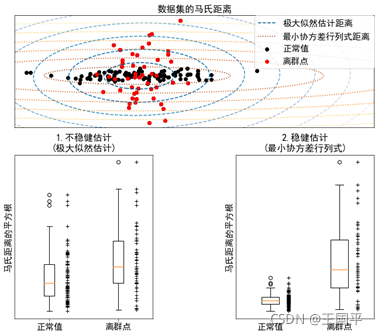








 该博客介绍了如何使用scikit-learn的EllipticEnvelope进行离群点检测。通过对比标准估计和稳健估计(最小协方差行列式)在处理带有离群点的数据集时的效果,展示了稳健估计在处理异常值影响下的优势。案例中,通过生成含有离群点的二维数据,计算并可视化了两种方法的马氏距离,揭示了最小协方差行列式在识别离群点上的精确性。
该博客介绍了如何使用scikit-learn的EllipticEnvelope进行离群点检测。通过对比标准估计和稳健估计(最小协方差行列式)在处理带有离群点的数据集时的效果,展示了稳健估计在处理异常值影响下的优势。案例中,通过生成含有离群点的二维数据,计算并可视化了两种方法的马氏距离,揭示了最小协方差行列式在识别离群点上的精确性。

















 689
689

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










