稀疏表示综述：A Survey of Sparse Representation: Algorithms and Applications_2015（2）

最新推荐文章于 2024-04-16 17:34:14 发布
最新推荐文章于 2024-04-16 17:34:14 发布
阅读量8.2k 收藏 44
点赞数 5
分类专栏： Paper Reading 文章标签： sparse strategy applications
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/shanglianlm/article/details/46866803
版权

稀疏表示综述：A Survey of Sparse Representation: Algorithms and Applications_2015（2）

本文地址：http://blog.csdn.net/shanglianlm/article/details/46866803

VI. 基于邻近算法的优化策略（PROXIMITY ALGORITHM BASED OPTIMIZATION STRATEGY）

proximity algorithm 的核心是 使用邻近算子（proximal operator）去迭代地求解子问题（sub-problem）。
proximity algorithm 被广泛地应用于求解非光滑（nonsmooth），约束凸优化问题（constrained convex optimization problems） [29]。

假设一个简单的约束优化问题
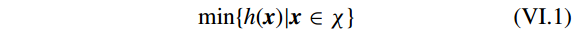
这里写图片描述
其中

了解本专栏 订阅专栏 解锁全文 超级会员免费看
mingo_敏
关注
  • 5
    点赞
  • 踩
  • 44
    收藏
    觉得还不错? 一键收藏
  • 打赏
    打赏
  • 1
    评论
专栏目录
订阅专栏
稀疏表示综述：A Survey of Sparse Representation: Algorithms and Applications_2015（1）
mingo_敏
07-12 6182
A Survey of Sparse Representation: Algorithms and Applications ZHENG ZHANG, YONG XU, JIAN YANG, XUELONG LI, AND DAVID ZHANG 本文地址：http://blog.csdn.net/shanglianlm/article/details/46848803
稀疏表示方法综述
10-28
稀疏表示作为阵列信号处理领域的重要研究方向，现在受到了越来越多人们的关注，这一综述有助于大家了解这一领域的研究进展。
稀疏表示
sulanqing的专栏
03-24 458
点击打开链接
稀疏表示综述
哇哦，小菜鸟
07-02 2880
哈工大徐勇发表在IEEE上面关于稀疏表示及其应用的综述性文章：A Survey of Sparse Representation: Algorithms and Applications。这是他的Homepage：http://www.yongxu.org/lunwen.html  里面有许多的代码和文章可以下载 A Survey of Sparse Representation: Algo
Simultaneous Localization And Mapping: A Survey of Current Trends in Autonomous Driving综述
何必浓墨重彩
04-26 6140
Abstract In this article, we propose a survey of the Simultaneous Localization And Mapping field when considering the recent evolution of autonomous driving. The growing interest regarding self-drivi...
【点云系列】综述： Deep Learning for 3D Point Clouds: A Survey
weixin_43882112的博客
12-03 4814
文章目录摘要简介：2 背景2.1 数据集2.2 衡量指标3 3D形状分类3.1基于多视角的方法3.2基于体素的方法3.3 基于点的方法3.3.1逐点MLP网络3.3.2基于卷积的网络3.3.3基于图的网络3.3.4基于数据索引的方法3.3.5其他方法小结4 3D物体检测与跟踪4.1 3D物体检测4.1.1 基于候选区域的方法4.1.2 single-shot方法4.2 3D对象跟踪4.3 3D场景流估计4.4 小结：5 3D点云分割5.1 3D 语义分割5.1.1 基于投影的方法5.1.2 基于离散的方法5
图像处理：张量分解在图像处理领域的应用
禅与计算机程序设计艺术
08-16 913
随着计算机视觉和图像处理技术的快速发展,图像数据呈现出高维、多模态、海量等特点。传统的矩阵分解方法已经无法有效处理这些复杂的图像数据。张量分解作为一种高阶矩阵分解方法,可以很好地捕捉图像数据的高维结构信息,在图像处理领域展现出巨大的应用前景。本节介绍几种常用的张量分解算法,包括高阶SVD(HOSVD)、Tucker-ALS、CP-ALS等。这些算法的核心思想是通过迭代优化的方式,交替更新张量分解的因子矩阵,直到收敛为止。综上所述,本文系统地介绍了张量分解技术在图像处理领域的应用。
稀疏编码
carina197834的专栏
02-03 1570
而每个神经元对这些刺激的表达则采用了稀疏编码(Sparse Coding, SC)原则,将图像在边缘、端点、条纹等方面的特性以稀疏编码的形式进行描述.从数学的角度来说,稀疏编码是一种多维数据描述方法,数据经稀疏编码后仅有少数分量同时处于明显激活状态,这大致等价于编码后的分量呈现超高斯分布.在实际应用中,稀疏编码有如下几个优点:编码方案存储能力大,具有联想记忆能力,并且计算简便;使自然信号的结构更加
稀疏编码(Sparse Coding)
qq_35608277的博客
06-16 3556
图像是有一些基的线性组合形成。自然图像是个稀疏结构，即任何给定图像都可以用大数据里面的少数几个描述符（基）来表示。寻找使得每个系数的概率分布是单模态并且在0处是峰分布的低熵（low-entropy）方法。 ref https://www.cnblogs.com/yifdu25/p/8128028.html http://www.360doc.com/content/14/0603/11/10724725_383221152.shtml http://freemind.pluskid.org/machine-
l1正则化的稀疏表示和l2正则化的协同表示
写代码的柯长的博客
04-12 5049
这些天一直在看稀疏表示和协同表示的相关论文，特此做一个记录： 这篇文章将主要讨论以下的问题： 1.稀疏表示是什么？ 2.l1正则化对于稀疏表示的帮助是什么，l0,l1,l2,无穷范数的作用？ 3.稀疏表示的robust为什么好？ 4.l2正则化的协同表示是不是比稀疏表示更好？ 好的，内容开始。 稀疏表示是什么？ 稀疏表示的基本思想来自压缩感知，即我们能用最少的样本来代表测试数据...
2020-2-14 深度学习笔记7 - 深度学习中的正则化4（稀疏表示-稀疏化激活单元(元素稀疏)，Bagging和其他集成方法，Dropout-廉价Bagging近似）
weixin_42555985的博客
03-01 1111
第七章 深度学习中的正则化 官网链接 2020-2-9 深度学习笔记7 - 深度学习中的正则化1（参数范数惩罚和范数惩罚约束） 2020-2-12 深度学习笔记7 - 深度学习中的正则化2（欠约束，数据集增强，噪声鲁棒性，输出目标注入噪声） 2020-2-13 深度学习笔记7 - 深度学习中的正则化3（半监督,多任务,提前终止-解决过拟合,参数绑定与参数共享） 稀疏表示 前文所述的权重衰减直接惩罚...
基于压缩感知和KSVD的图像去噪算法matlab仿真
fpga/matlab/simulink算法仿真工程
03-21 1009
Y为要表示的信号，D为超完备矩阵（列数大于行数）， X为系数矩阵，X与Y按列对应，表示D中元素按照Xi为系数线性组合为Y，我们的目的是找到让X尽量稀疏的D。字典是前辈们学习总结的精华，当我们需要学习新的知识的时候，不必与先辈们一样去学习先辈们所有学习过的知识，我们可以参考先辈们给我们总结的字典，通过查阅这些字典，我们可以大致学会到这些知识。我们通常会要求的我们的字典尽可能全面，也就是说总结出的字典不能漏下关键的知识点。查字典的时候，我们想要我们查字典的过程尽可能简洁，迅速，准确。即，查字典要快、准、狠。
OMP和KSVD在图像稀疏表示和字典学习中的理解
wmz13248的博客
08-12 1988
最近学习稀疏表示和字典学习，了解到了OMP算法和KSVD算法，看了大量资料，理解如下： 1. OMP算法： *可以解决的问题：* 已知过完备字典D，和输入图像y，通过公式 y=Dx求出稀疏系数x，其中，y是已经转换为列向量的图像 参考学习资料：https://blog.csdn.net/u010381985/article/details/60571570?ops_request_misc=%257B%2522request%255Fid%2522%253A%25221597198993197
【信道估计】MIMO4x4系统下对ZFMMSEML等线性预编码算法误码率性能的比较附matlab代码
最新发布
Matlab_dashi的博客
04-16 1092
在多输入多输出 (MIMO) 系统中，信道估计是提高系统性能的关键技术。线性预编码算法是一种有效的信道估计方法，它通过在发送端对数据进行预编码，来提高接收端的信噪比。本文针对 MIMO 4x4 系统，对 ZF-MMSE-ML 等线性预编码算法的误码率性能进行了比较。通过仿真，分析了不同信道条件和不同算法参数对误码率的影响。结果表明，ZF-MMSE-ML 算法在高信噪比条件下具有较好的误码率性能，而 MMSE 算法在低信噪比条件下表现更佳。
Variable Selection via Nonconcave PenalizedLikelihood and its Oracle Properties 论文解析-特征选择的Oracle特性-1
fangfanglovezhou的博客
05-23 942
特征选择的Oracle特
梯度下降、ISTA和FISTA算法收敛速率推导
xyjaixuexi的博客
10-17 1117
梯度下降法收敛速率 假设是凸可微的，并且满足。 即是利普希茨连续（）。 定理：固定步长的梯度下降法满足, 即梯度下降的收敛速率为。 证明： 由满足利普希茨条件 , （4.22） 将代入 , 利用的凸性有： 即, 取所以有： , （4.23） 由于 , （4.24） （4.24）的证明如下： , （4.25） 所以有 , （4.26） 令对（4.26）从0到k-1迭代求和有 , （4.27） 因为凸函数的目标函数总是减小的即 ...
最优化算法目录_python或matlab实现
眰恦
04-14 1800
通过学习最优化计算方法，使用python实现里面的基本算法。
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

mingo_敏

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值