参数估计方法详解-CSDN博客

一、什么是参数估计

我们建立一个含有众多参数的深度学习模型之后，需要通过多次的训练来找到最适合现实情况的那几组参数，所以模型的训练过程可以看作是参数估计（parameter estimation）。在统计概率学中对于参数估计的假设有两种不同的观点：

频率主义学派（Frequentist）认为参数虽然未知，但却是客观存在的固定值，因此，可通过优化似然函数等准则来确定参数值
贝叶斯学派（Beyesian）则认为参数是未观察到的随机变量，其本身也可有分布，因此，可假定参数服从一个先验分布，然后基于观测到的数据来计算参数的后验分布。

二、方法

参数估计的方法主要有以下几种：

最大似然估计MLE
最大后验估计MAP
贝叶斯估计
最小二乘估计

三、方法介绍

最大似然估计MLE：

频率主义学派，根据数据采样来估计频率分布参数。

最大似然估计，通俗理解来说，假定整体模型分布已知，利用已知的样本结果信息，反推最有可能导致这些样本结果出现的模型参数值！(估计值使得样本事件发生的可能性最大)

换句话说，最大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。

假设m个样本的数据集，独立地由未知真实数据生成分布生成。是一族由θ确定在相同空间上的概率分布。对θ的最大似然估计：

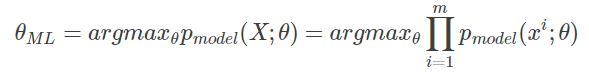
由于log不会改变函数的单调性，因此多个概率的乘积中可以转化为log，将乘法变换为加法：

重新缩放代价函数，除以m得到和训练数据经验分布相关的期望：

最大似然估计中，参数θ是一个固定的值，只需要满足最大化样本出现的可能即可，因此在样本的数量以及深度较小时，很容易出现过拟合的趋势。

例子：

以扔硬币的伯努利实验为例子，N次实验的结果服从二项分布，参数为P，即每次实验事件发生的概率，不妨设为是得到正面的概率。为了估计P，采用最大似然估计，似然函数可以写作

其中表示实验结果为i的次数。下面求似然函数的极值点，有

得到参数p的最大似然估计值为

可以看出二项分布中每次事件发的概率p就等于做N次独立重复随机试验中事件发生的概率。

如果我们做20次实验，出现正面12次，反面8次

那么根据最大似然估计得到参数值p为12/20 = 0.6。

-----------------------✂---------------------------

最大后验估计MAP

贝叶斯派将参数θ作为随机变量，服从某一分布。正因为参数是不固定的，所以用概率p(x)的方式来表达。我们希望求出观察到样本x的情况下，θ的分布情况p(θ|x)。此时不是要求似然函数最大，而是要求由贝叶斯公式计算出的整个后验概率最大。根据贝叶斯定理可得θ关于x的后验概率：

要对这个后验概率求最大值：

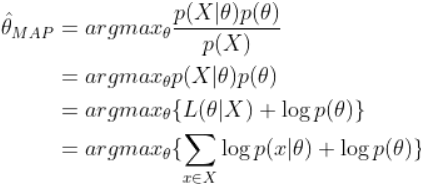
等式第一项的分母p(X)很难计算，而且它是与最优化θ是无关的，而我们只关心最优θ（p(x)相同）。在这种情况下，我们采用了一种近似的方法求后验概率，即舍弃分母，直接对分子做最大似然估计，这就是等式第二项的最大后验估计。

最大后验估计相比最大似然估计，只是多了一项先验概率P（θ），这个先验可以用来描述人们已经知道或者接受的普遍规律，它正好体现了贝叶斯认为参数也是随机变量的观点，在实际运算中通常通过超参数给出先验分布。最大似然估计其实是经验风险最小化的一个例子，而最大后验估计是结构风险最小化的一个例子。如果样本数据足够大，最大后验概率和最大似然估计趋向于一致，如果样本数据为0，最大后验就仅由先验概率决定。尽管最大后验估计看着要比最大似然估计完善，但是由于最大似然估计简单，很多方法还是使用最大似然估计。

例子：

在扔硬币的试验中，每次抛出正面发生的概率应该服从一个概率分布，这个概率在0.5处取得最大值，这个分布就是先验分布。先验分布的参数我们称为超参数(hyperparameter)。

下面我们仍然以扔硬币的例子来说明，我们期望先验概率分布在0.5处取得最大值，我们可以选用Beta分布即

其中Beta函数展开是

当x为正整数时

Beta分布的随机变量范围是[0,1],所以可以生成normalised probability values。下图给出了不同参数情况下的Beta分布的概率密度函数

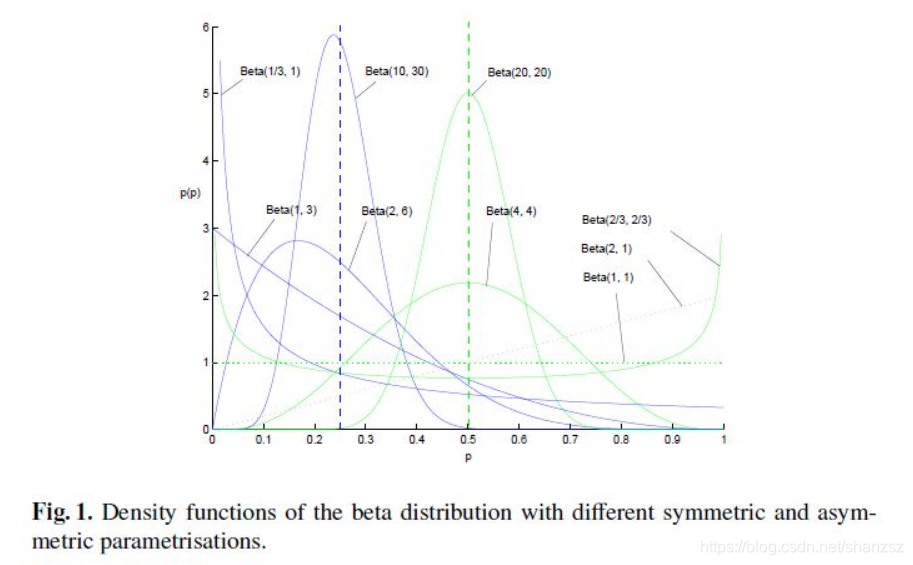
我们取,这样先验分布在0.5处取得最大值，现在我们来求解MAP估计函数的极值点，同样对p求导数我们有

得到参数p的的最大后验估计值为

和最大似然估计的结果对比可以发现结果中多了这样的pseudo-counts,这就是先验在起作用。并且超参数越大，为了改变先验分布传递的belief所需要的观察值就越多，此时对应的Beta函数越聚集，紧缩在其最大值两侧。如果我们做20次实验，出现正面12次，反面8次，那么那么根据MAP估计出来的参数p为16/28 = 0.571,小于最大似然估计得到的值0.6，这也显示了“硬币一般是两面均匀的”这一先验对参数估计的影响。

-----------------------✂---------------------------

贝叶斯估计

贝叶斯估计的思想：先验分布 + 样本信息后验分布

上述思考模式意味着，新观察到的样本信息将修正人们以前对事物的认知。换言之，在得到新的样本信息之前，人们对的认知是先验分布，在得到新的样本信息后，人们对的认知为。而后验分布一般也认为是在给定样本的情况下的条件分布，而使达到最大的值称为最大后验估计。

其实可以认为贝叶斯估计是在MAP上做进一步拓展（也可以认为在贝叶斯估计的基础上将参数确定化为一个值，通过最大化这个值，也就是极大似然法，实现了最大后验估计），此时不直接估计参数的值，而是允许参数服从一定概率分布。也就是说我们不能在忽略分母，需要将分母计算出来。回顾一下贝叶斯公式

通过全概率公式求分母

我们仍然以扔硬币的伯努利实验为例来说明。和MAP中一样，我们假设先验分布为Beta分布，但是构造贝叶斯估计时，不是要求用后验最大时的参数来近似作为参数值，而是求满足Beta分布的参数p的期望，有

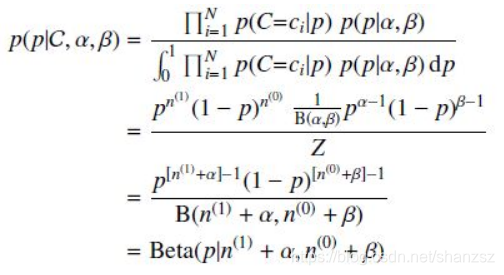
注意这里用到了公式

根据贝叶斯估计，参数p服从一个新的Beta分布。

回忆一下，我们为p选取的先验分布是Beta分布，然后以p为参数的二项分布用贝叶斯估计得到的后验概率仍然服从Beta分布，由此我们说二项分布和Beta分布是共轭分布。在概率语言模型中，通常选取共轭分布作为先验，可以带来计算上的方便性。最典型的就是LDA中每个文档中词的Topic分布服从Multinomial分布，其先验选取共轭分布即Dirichlet分布；每个Topic下词的分布服从Multinomial分布，其先验也同样选取共轭分布即Dirichlet分布。

根据Beta分布的期望和方差计算公式，我们有

可以看出此时估计的p的期望和MLE ，MAP中得到的估计值都不同，此时如果仍然是做20次实验，12次正面，8次反面，那么我们根据贝叶斯估计得到的p满足参数为12+5和8+5的Beta分布，其均值和方差分别是17/30=0.567, 17*13/(31*30^2)=0.0079。可以看到此时求出的p的期望比MLE和MAP得到的估计值都小，更加接近0.5。

综上所述我们可以可视化MLE,MAP和贝叶斯估计对参数的估计结果如下

例子：

假设中国的大学只有两种：理工科和文科，这两种学校数量的比例是1:1，其中，理工科男女比例7:1，文科男女比例1:7。某天你被外星人随机扔到一个校园，问你该学校可能的男女比例是多少？然后，你实际到该校园里逛了一圈，看到的5个人全是男的，这时候再次问你这个校园的男女比例是多少？

因为刚开始时，有先验知识，所以该学校的男女比例要么是7:1，要么是1:7，即P(比例为7:1) = 1/2，P(比例为1:7) = 1/2。
然后看到5个男生后重新估计男女比例，其实就是求P(比例7:1|5个男生）= ？，P(比例1:7|5个男生) = ？
用贝叶斯公式，可得：P(比例7:1|5个男生) = P(比例7:1)*P(5个男生|比例7:1) / P(5个男生)，P(5个男生)是5个男生的先验概率，与学校无关，所以是个常数；类似的，P(比例1:7|5个男生) = P((比例1:7)*P(5个男生|比例1:7)/P(5个男生)。
最后将上述两个等式比一下，可得：P(比例7:1|5个男生)/P(比例1:7|5个男生) = {P((比例7:1)*P(5个男生|比例7:1)} / { P(比例1:7)*P(5个男生|比例1:7)}。（看看两种的可能性占到多少）

贝叶斯估计的形象解释：

我去一朋友家：

按照频率派的思想，我估计他在家的概率是1/2，不在家的概率也是1/2，是个定值。

按照贝叶斯派的思想，他在家不在家的概率不再认为是个定值1/2，而是随机变量。比如按照我们的经验（比如当天周末），猜测他在家的概率是0.6，但这个0.6不是说就是完全确定的，也有可能是0.7。如此，贝叶斯派没法确切给出参数的确定值（0.3,0.4，0.6,0.7，0.8,0.9都有可能），但至少明白哪些取值（0.6,0.7，0.8,0.9）更有可能，哪些取值（0.3,0.4）不太可能。进一步，贝叶斯估计中，参数的多个估计值服从一定的先验分布，而后根据实践获得的数据（例如周末不断跑他家），不断修正之前的参数估计，从先验分布慢慢过渡到后验分布。

四、区别

首先我们可以看到,最大似然估计和最大后验估计都是基于一个假设，即把待估计的参数π看做是一个固定的值，只是其取值未知。

最大似然是最简单的形式，其假定参数虽然未知，但是是确定值，就是找到使得样本对数似然分布最大的参数。而最大后验，只是优化函数为后验概率形式，多了一个（向似然函数添加）先验概率项。

而贝叶斯估计和二者最大的不同在于，它假定参数是一个随机的变量，不是确定值。在样本分布P(π|χ)上，π是有可能取从0到1的任意一个值的，只是取到的概率不同。而MAP和MLE只取了整个概率分布P(π|χ)上的一个点，丢失了一些观察到的数据χ给予的信息（这也就是经典统计学派和贝叶斯学派最大的分歧所在。）