编程实现“斐波那契数列”的5种方法！ | 经典面试题

编程求值斐波那契数列f(n)，是面试中，非常常见的题目。

什么是斐波那契数列？

斐波那契数列是这样一个数列，它满足：

f(0) = 0;

f(1) = 1;

f(n) = f(n-1) + f(n-2)  (当n>=2时)

到底有几种方法，这些思路里蕴含的优化思路究竟是怎么样的，今天和大家聊一聊。

一、递归法

伪代码：

uint32_t f(uint32_t n){

    if(n==0) return 0;

    if(n==1) return 1;

    return f(n-1)+f(n-2);

}

思路：这是一个递归的代码，非常清晰，直接把斐波那契数列的定义翻译成了代码。

例如：

假设要求f(5)

f(5) = f(4) + f(3);

于是会递归计算f(4)和f(3);

接着要求f(4)

f(4) = f(3)+ f(2);

于是会递归计算f(3)和f(2);

可以看到，计算f(5)和f(4)中都要计算f(3)，但这两次f(3)会重复计算，这就是递归的最大问题，对于同一个f(a)，不能复用。

计算一个f(n)到底需要有多少次递归调用呢？

我们可以在代码里加一个计数验证一下。

伪代码：

static uint32_t count=0; // 加一个全局变量计数

uint32_t f(uint32_t n){

    count++;  // 递归一次，计数加一

    if(n==0) return 0;

    if(n==1) return 1;

    return f(n-1)+f(n-2);

}

实验的结果：

f(5) count = 15

f(10) count = 177

f(15) count = 1K+

f(20) count = 2W+

f(25) count = 24W+

f(30) count = 269W+

f(35) count = 2986W+

f(40) count = 3.3Y+

f(45) … 抱歉，我机器太慢，算不出来

额滴神哪，不是骗我吧！！！

画外音：

（1）这个count，是函数递归了对少次；

（2）f(45)，机器居然算不出来；

（3）对结论有疑问的，自己可以run一把；

启示：

（1）斐波那契数列求解，如果用直接法，时间复杂度是指数级的，不可行；

（2）如果没有太大的把握，工程中尽量少使用递归，容易把自己玩死；

二、正推法

从斐波那契数列的定义：

f(0) = 0;

f(1) = 1;

f(n) = f(n-1) + f(n-2) n>=2时

可以看出，每一个新的f(n)，是前两个旧的f(n-1)和f(n-2)之和，一路递归下去，最终都将递归到f(0)和f(1)上来。

反过来想，我们不倒着f(n),f(n-1),f(n-2)这么计算，而是f(0),f(1),f(2)…f(n)这么正向计算，岂不是更快么？

伪代码：

uint32_t f(uint32_t n){

   uint32_t arr[n];

   arr[0]=0;

   arr[1]=1;

   for(uint32_t i=2;i<=n;i++){

       arr[i]=arr[i-1]+arr[i-2];

    }

   return arr[n];

}

这么正向的计算，只需要一个for循环，就能够计算出f(n)的值，时间复杂度是O(n)。

三、通项公式法

f(0) = 0;

f(1) = 1;

f(n) = f(n-1) + f(n-2)  (当n>=2时)

大学学过相关课程，可解出f(n)通项公式。

画外音：额，是不是有朋友读了个假大学。

线性递推数列：

f(n) = f(n-1) + f(n-2)

对应的特征方程是：

x^2 = x + 1

求解特征方程得到：

x1=(1+√5)/2

x2=(1-√5)/2

于是得到：

f(n) = a1(x1)^n + a2(x2)^n

将：

f(0) = 0;

f(1) = 1;

代入上述通项公式。

于是得到：

a1=1/√5

a2=-1/√5

于是最终得到：

f(n)=(1/√5)*{[(1+√5)/2]^n -[(1-√5)/2]^n}

画外音：别问我为什么懂这些，我TM作为计算机信息安全专业，也被数论，有限域，加密解密这些数学学科折磨过。

可忽略上述吹牛*的过程，百度一下能得到答案。

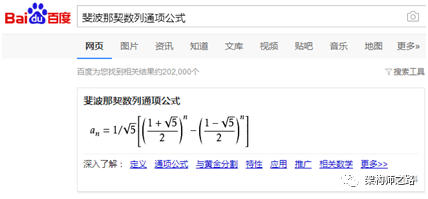
总之，得到了斐波那契数列通项公式：

f(n) = a1(b1)^n + a2(b2)^n

其中a1, b1, a2, b2四个数字都是常数。

想求f(45)，把n=45带入上述通项公式即可。

那么，带入通项公式求解，时间复杂度是多少呢？是O(1)么？

通项公式的计算，并不能O(1)得到，而是一个a^n，即power(a, n)的求解过程。

那么，如何求解a的n次方呢？

最粗暴的方法，将a不断的自乘n次。

伪代码：

uint64_t power(uint64_t a, uint64_t n){

   uint64_t result=a;

   for(uint64_t i=1;i<n;i++){

       result *=a;

    }

   return result;

}

很容易知道，a通过for循环不断自乘，求解a^n的时间复杂度是O(n)。

你TM在逗我！！！

通过“正推”法，求解f(n)的时间复杂度是O(n)。

楼主搞了这么久的奇技淫巧，搞什么“通项公式法”，结果也是个O(n)的方法？？？

不不不，稍安勿躁，上面讲的都是思路，求解a^n，可以使用之前文章里说过的减治法。

还记得分治法与减治法的区别么？

（1）减治法，大问题分解为小问题，小问题只要递归一个分支，例如：二分查找，随机选择；

（2）分治法，大问题分解为小问题，小问题都要迭代各个分支，例如：快速排序

具体在《一次搞透，面试中的TopK问题！随机选择时详细介绍过；

a^n减治法思路：

（1）当n是偶数时，先求出r=a^(n/2)，再做一次r*r的计算，就得到了a^n；

（2）当n是奇数时，n-1就一定是偶数，先求出r=a^(n-1)/2，在做一次r*r*a，就得到了a^n；

伪代码：

uint64_t power(uint64_t a, uint64_t n){

    if(n==0)return 1;

    if(n==1)return a;

   uint64_t r=0;

   if(n%2){

       r=power(a, (n-1)/2);

       return r*r*a;

    }

   else{

       r=power(a, n/2);

       return r*r;

    }

}

每次将计算规模减半，是不是和二分查找很像？减治法求a^n的时间复杂度是O(lg(n))。

四、查表法

关键时刻，空间换时间的方法就出场了，如果有相对充裕的内存，可以有更快的算法。

思路：f(n)，一旦n的值确定，f(n)也就确定，可以提前计算好结果数组：

result[0]=0;

result[1]=1;

result[2]=1;

result[3]=2;

result[4]=3;

…

求f(n)时直接打表即可，伪代码：

return result[n];

打表的时间复杂度是O(1)。

画外音：但次都是查表，太没有意思了。

五、总结

斐波那契数列，不难；

但其思路有优化过程，并不简单：

（1）递归法，f(45)能跑得死机；

（2）正推法，O(n)，正推计算，有点意思；

（3）通项公式，本质转化为求a^n；

（4）减治法求a^n，O(lg(n))；

（5）打表法，O(1)，空间换时间；

画外音：注意，面试现场求解通项公式，有可能会吓到面试官，请慎用。

知其然，知其所以然。思路比结论重要。

架构师之路-分享可落地的架构文章

推荐阅读：

《世界上最美的排序算法！》

《世界上最慢的排序算法！》

《世界上最开脑洞的排序算法！

希望大家对“斐波那契数列”有新的认识，谢转。