Python 逻辑回归

                                Python 逻辑(斯蒂)回归

1 声明

本文的数据来自网络，部分代码也有所参照，这里做了注释和延伸，旨在技术交流，如有冒犯之处请联系博主及时处理。

2 逻辑斯蒂回归简介

相关概念见下：

某个事件发生的概率定义为P，P的范围是[0,1]

Odds = 一个事件发生的概率/不发生的概率 = 

针对P不等于0和1的情况，我们会发现P趋于“极小”时（即无限接近0）时odds仍无限趋向于0;P趋于“极大”时（即无限接近1）时odds趋向于+∞,即Odds的变化范围由[0, ∞]。

Logit 可以粗暴的理解为Log “it”（Odds）,优势（胜率），当它大于1时成功比失败的概率大。所以有 Logit = ln(Odds)=ln(P/(1-P))，这里不难发现对Odds取对数后其变化范围由 [0, ∞]变换为[-∞, ∞]与X的范围一致。

这时我们就可以建立X和Logit(“y”)的线性关系，而不能直接建立X与P(区间是0，1)的线性关系，因为二者的范围不一致。

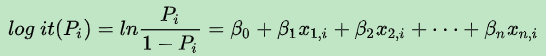
进而我们得到如下形式：

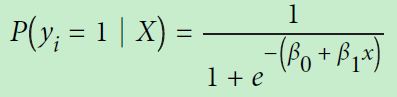
这里 是第i个观测的目标变量 是1的概率，它的范围是[0,1]。 是训练数据， 和 模型学习到的参数。一般我们设个阀值为0.5，大于0.5则目标变量的类是1，反之为0。

逻辑斯蒂（又称Sigmoid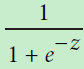） 是一个S形曲线的数学函数，它的值域是[0,1]

尽管有回归这个名词，但逻辑回归其实是个应用广泛的二分类算法。

针对多分类的情况可以通过one vs rest和MLR解决：

one vs rest(一对剩余)

一种应用在二分类之上的多分类的思想，如果有n个多分类，则可以分出 种即n种二分类(对应n个特征)，这个n个二分类应用逻辑回归的思路计算各个特征对应分类的概率，设置个阀值，取概率最大的特征所在的类为最终类。这里假设特征间相互独立。

one vs one（一对一）

同理这里的一对一思路类似one vs rest，只不过这里的粒度是单特征,会有 种情况。这里先对每个二分类取出分类值，综合所有情况“投票”（即统计出分类值最多）出最终类。

multinomial logistic regression (MLR)

该方法的逻辑斯蒂（回归分类函数）用下图的softmax函数。Softmax函数把输出映射成区间在(0,1)的值，并且做了归一化，所有元素的和累加起来等于1。所以可以直接当作概率对待，选取概率最大的分类作为预测的目标。

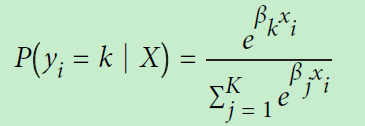
这里 是第i个观测的目标值的概率， 对应多分类k，K是所有分类的总和（即多少种分类）。

3 逻辑回归代码与注释示例

# 加载包
from sklearn.linear_model import LogisticRegression
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
# 加载鸢尾花数据
iris = datasets.load_iris()
features = iris.data
target = iris.target
# 标准化数据
scaler = StandardScaler()
features_standardized = scaler.fit_transform(features)
# 创建平通逻辑回归(二分类),注意数据集须是仅有两个的情况
#logistic_regression = LogisticRegression(random_state=0)
# 创建one-vs-rest ovr类型的逻辑回归(多分类),multinomial logistic regressiond的参数是multinomial
logistic_regression = LogisticRegression(random_state=0, multi_class="ovr")
# 训练模型
model = logistic_regression.fit(features_standardized, target)

​

4 总结

无