
GB, 梯度提升,通过进行M次迭代,每次迭代产生一个回归树模型,我们需要让每次迭代生成的模型对训练集的损失函数最小,而如何让损失函数越来越小呢?我们采用梯度下降的方法,在每次迭代时通过向损失函数的负梯度方向移动来使得损失函数越来越小,这样我们就可以得到越来越精确的模型。
假设GBDT模型T有4棵回归树构成:t1,t2,t3,t4,样本标签为Y(y1,y2,y3,.....yn)
设定该模型的误差函数为L,并且为SquaredError,则整体样本的误差推导如下:
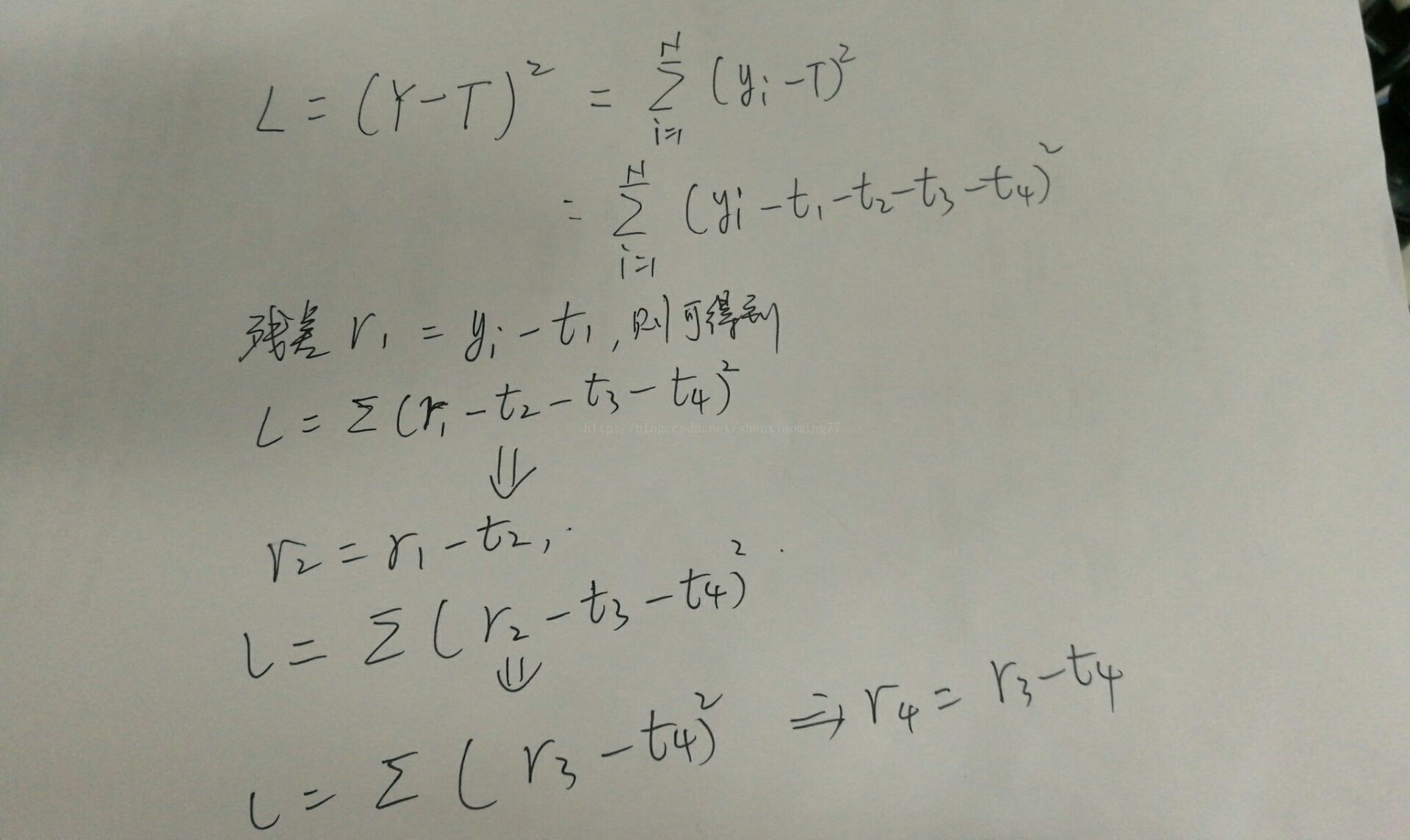
对于首棵树,可以看出,拟合的就是训练样本的标签,并且得到t1预测后的残差,从误差函数的公式中可以看出,后面的残差r2 = r1 - t2, r3 = r2 - t3, r4 = r3 - t4....,由此可以得出,后面的回归树t2, t3, t4创建时 都是为了拟合前一次留下的残差,可以看出,残差不断在减小,直至达到可接受的阈值为止。
对于梯度版本,采用误差函数的当前负梯度值作为当前模型预测留下的残差,因此创建新的一棵回归树来拟合该残差,更新后,整体gbdt模型的残差将进一步降低,也带来L的不断降低
gbdt树分为两种,
(1)残差版本
残差其实就是真实值和预测值之间的差值,在学习的过程中,首先学习一颗回归树,然后将“真实值-预测值”得到残差,再把残差作为一个学习目标,学习下一棵回归树,依次类推,直到残差小于某个接近0的阀值或回归树数目达到某一阀值。其核心思想是每轮通过拟合残差来降低损失函数。
总的来说,第一棵树是正常的,之后所有的树的决策全是由残差来决定。
(2)梯度版本
与残差版本把GBDT说成一个残差迭代树,认为每一棵回归树都在学习前N-1棵树的残差不同,Gradient版本把GBDT说成一个梯度迭代树,使用梯度下降法求解,认为每一棵回归树在学习前N-1棵树的梯度下降值。总的来说两者相同之处在于,都是迭代回归树,都是累加每颗树结果作为最终结果(Multiple Additive Regression Tree),每棵树都在学习前N-1棵树尚存的不足,从总体流程和输入输出上两者是没有区别的;
两者的不同主要在于每步迭代时,是否使用Gradient作为求解方法。前者不用Gradient而是用残差—-残差是全局最优值,Gradient是局部最优方向*步长,即前者每一步都在试图让结果变成最好,后者则每步试图让结果更好一点。
两者优缺点。看起来前者更科学一点–有绝对最优方向不学,为什么舍近求远去估计一个局部最优方向呢?原因在于灵活性。前者最大问题是,由于它依赖残差,cost function一般固定为反映残差的均方差,因此很难处理纯回归问题之外的问题。而后者求解方法为梯度下降,只要可求导的cost function都可以使用。











 本文深入解析了GBDT(Gradient Boosting Decision Tree)的工作原理,包括残差版本和梯度版本的区别,以及它们如何通过迭代逐步减少残差来优化模型。
本文深入解析了GBDT(Gradient Boosting Decision Tree)的工作原理,包括残差版本和梯度版本的区别,以及它们如何通过迭代逐步减少残差来优化模型。
















 2021
2021

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








