Introduction
通常,我们对发生在时间域上的事件希望可以找到合适的模式来描述。考虑下面一个简单的例子,比如有人利用海草来预测天气,民谣告诉我们说,湿漉漉的海草意味着会下雨,而干燥的海草意味着会天晴,而如果海草不是很湿也不是很干燥,比如潮湿的状态,那么我们恐怕很难断定天气会怎样,可能下雨也可能天晴,我们或许可以根据昨天的天气来进行判断,根据昨天的天气和今天海草的状态,或许可以有一个更好的预测。
上面介绍的预测系统,就是我们接下来要探讨的模型的一个典型例子。在这个教程中,我们主要探讨以下几个问题:
1: 首先我们要介绍在时间域上形成概率模式的系统,比如上面提到的天气预测。
2: 然后我们会看到,在这个系统里,我们观察到的并不是我们想要预测的,我们想要预测
的模式是隐藏的,比如上面的天气预测,我们观察到的是海草的状态,但是我们要预测的是天气。
3: 最后我们会看看这个系统能够解决的一些问题,比如上面的天气预测,如何根据海草一个
礼拜的状态来判断这个礼拜的天气,如何根据海草一段时间的状态确定现在所处的季节等。
Generating Patterns
考虑一组交通灯,通常情况下,交通灯的顺序可以表示为:红灯-绿灯-黄灯然后又转回红灯,交通灯的状态可以用状态机来表示,我们可以注意到,每个状态只与之前的状态决定,就是说如果当前状态是红灯,那么下一个状态一定是绿灯,这种系统称为确定性系统,因为状态之间的转换是确定的。
再来看看另外一个例子,就是之前提到的天气预测,我们假设有三种天气:晴天,雨天和多云。一般来说,我们都知道,这三种天气之间没有确定的转换关系,晴天之后可能是雨天,也可能是多云,这种系统就是不确定性系统,因为状态之间的转换是不确定的。很明显,如果不做任何假设,我们无法建立一个有效地模型去模拟这类系统。
一个可能的解决方案就是就是加入某些假设,将不确定性系统当成确定性系统来对待,我们假设系统的当前状态取决于系统的前一状态,这个假设称为马尔科夫假设,这个假设使得问题大大简化了,但是当然代价就是丢失了很多信息。虽然这个假设很多时候和实际不符,但是这个假设却能有效地解决很多实际问题,即使它建立的模型做出的预测不是完全正确的。
Markov Process
在一个马尔科夫过程中,一个状态转移到下一个状态的概率,取决于之前的n个状态,这个过程称为n阶模型,n表示影响状态转换的其它状态的个数。最简单的马尔科夫过程是一阶过程模型,意味着当前状态只取决于前面的一个状态。
注意到,对于有
M
个状态的一阶马尔科夫过程,存在
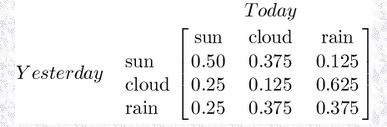
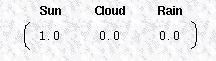
从转换矩阵可知,如果昨天是晴天,那么今天是晴天的概率是0.5,而今天是多云的概率是0.375,注意每一行的概率之和应该都为1. 我们需要对这样一个系统定义一个初始状态,我们用一个向量 π 来表示这个系统的初始状态,如下所示:
从系统的初始状态可以看出,今天为晴天的概率是1。
现在,我们定义了一个一阶的马尔科夫过程,它包括
1: 状态:三个状态——晴天,雨天,多云。
2: 初始向量:用来描述系统所含初始状态的概率。
3: 状态转换矩阵:描述每个状态之间相互转换的概率。
Limitations of a Markov Process
前面我们介绍了马尔科夫过程,并且了解了马尔科夫过程的几个要素:比如初始状态,转换矩阵等等。利用马尔科夫过程,可以对一些连续发生的事件做预测。但是有的时候,有些模式利用马尔科夫过程不能有效地进行描述,比如前面的天气预测系统,为了预测今天的天气,我们需要知道昨天的天气以及转换矩阵,但是有的时候我们不知道昨天的天气,只能知道海草的状态,民谣告诉我们,海草的状态和天气是紧密相关的。这种情况下,我们有两类状态,一类是可观察的(海草的状态),另一类是隐藏的(当天的天气),我们希望可以设计一个模型,能够基于海草的状态和马尔科夫假设来预测天气,而不需要知道之前的天气情况。
我们仍然以天气预测系统为例,假设有三种天气(即三个隐藏变量)需要预测(晴天,雨天,多云),而可观察的变量:即海草的状态有四种(dry, dryish, damp,soggy),我们可以发现,可观察变量的个数与隐藏变量的个数是不一样的,而可观察变量的转换过程与隐藏变量的转换过程存在一定的联系,我们利用隐马尔科夫模型
来模拟这类系统,在隐马尔科夫模型中,有一个隐马尔科夫过程,而可观察变量与隐藏变量是有联系的。
Hidden Markov Models
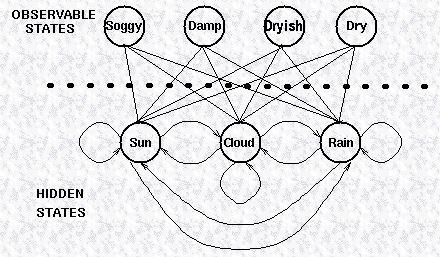
下图显示了天气预测系统中,可观察变量(海草的状态)与隐藏变量(天气情况)之间的转换关系,隐藏变量之间的转换是由一个简单的一阶马尔科夫过程来描述。
图中,可观察变量与隐藏变量之间的连线表示当隐马尔科夫过程处于某一特定状态时,生成某一对应可观察变量的概率。一个可观察变量可能由任何一个隐藏变量
生成,所以生成该可观察变量的概率之和应该为1。即
Pr(Obs|Sun)+Pr(Obs|Rain)+Pr(Obs|Cloud)=1
。
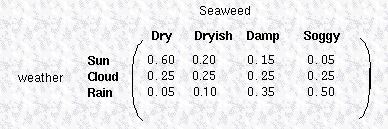
除了定义马尔科夫过程的概率,我们还定义了隐藏变量与可观察变量之间的转换关系,用一个矩阵表示,称为confusion矩阵,如下图所示:
我们可以看到,其每一行的和为1。
Summary
我们已经看到,隐马尔科夫模型包含以下几个要素:
隐藏状态:系统真正需要预测的状态,可以用一个马尔科夫过程描述。
可观察状态:系统显露出来的状态。
初始向量:用来描述系统中隐含模型在某一特定初始隐藏状态的概率。
状态转换矩阵:描述每个状态之间相互转换的概率。
confusion 矩阵:包含系统隐含模型在隐藏状态下生成可观察状态的概率。
所以简单来说,一个隐马尔科夫模型是一个标准的马尔科夫过程,加上一系列可观察的状态,以及可观察状态与隐藏状态的联系(用概率表示)。
参考来源:
http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html






















 1426
1426

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








