机器学习算法笔记系列之深入理解主成分分析PCA-原理篇

Author: shizhixin
Blog: http://blog.csdn.net/shizhixin
Weibo：http://weibo.com/zhixinshi
Email: zstarstone@163.com
Date: 2016-04-14
Note: 本笔记是本人根据网上和书本资料总结，并对所有作者表示感谢，特别感谢致谢文献中提到的作者！本笔记仅供学习交流！

1 概述

真实的训练数据总是存在各种各样的问题：

1、 比如拿到一个汽车的样本，里面既有以“千米/每小时”度量的最大速度特征，也有“英里/小时”的最大速度特征，显然这两个特征有一个多余。

2、 拿到一个数学系的本科生期末考试成绩单，里面有三列，一列是对数学的兴趣程度，一列是复习时间，还有一列是考试成绩。我们知道要学好数学，需要有浓厚的兴趣，所以第二项与第一项强相关，第三项和第二项也是强相关。那是不是可以合并第一项和第二项呢？

3、 拿到一个样本，特征非常多，而样例特别少，这样用回归去直接拟合非常困难，容易过度拟合。比如北京的房价：假设房子的特征是（大小、位置、朝向、是否学区房、建造年代、是否二手、层数、所在层数），搞了这么多特征，结果只有不到十个房子的样例。要拟合房子特征->房价的这么多特征，就会造成过度拟合。

4、 这个与第二个有点类似，假设在IR中我们建立的文档-词项矩阵中，有两个词项为“learn”和“study”，在传统的向量空间模型中，认为两者独立。然而从语义的角度来讲，两者是相似的，而且两者出现频率也类似，是不是可以合成为一个特征呢？

5、 在信号传输过程中，由于信道不是理想的，信道另一端收到的信号会有噪音扰动，那么怎么滤去这些噪音呢？

而这里的特征很多是和类标签有关的，但里面存在噪声或者冗余。在这种情况下，需要一种特征降维的方法来减少特征数，减少噪音和冗余，减少过度拟合的可能性。

下面探讨一种称作主成分分析（PCA）的方法来解决部分上述问题。PCA的思想是将n维特征映射到d维上$(d < n)$，这d维是全新的正交特征。这d维特征称为主元，是重新构造出来的d维特征，而不是简单地从n维特征中去除其余n-d维特征。

2 引言

内积与投影

---

导读：大部分人估计都知道PCA是将数据点向新的方差最大的单位向量做投影，但是什么是到向量的投影，它和内积又有什么关系呢？

两个向量的内积定义为：

$(a_1,a_2,\cdots,a_n)^\mathsf{T}\cdot (b_1,b_2,\cdots,b_n)^\mathsf{T}=a_1b_1+a_2b_2+\cdots+a_nb_n$

两个向量的内积是一个实数，从数学计算的角度很容易计算出两个向量的内积，但是怎么从几何意义上理解内积呢？
为了简单，看二维向量的内积。假设有两个向量 $A=(x_1,y_1)^T$ 和 $B=(x_2,y_2)^T$ ，从 A 点对 OB 向量做一条垂线，垂线与 OB 的交点C即为 A 在 B 上的投影，再设 A 与 B 的夹角是 $\alpha$，那么点 A 到 B 的投影长度即为 $|A|cos(\alpha)$。

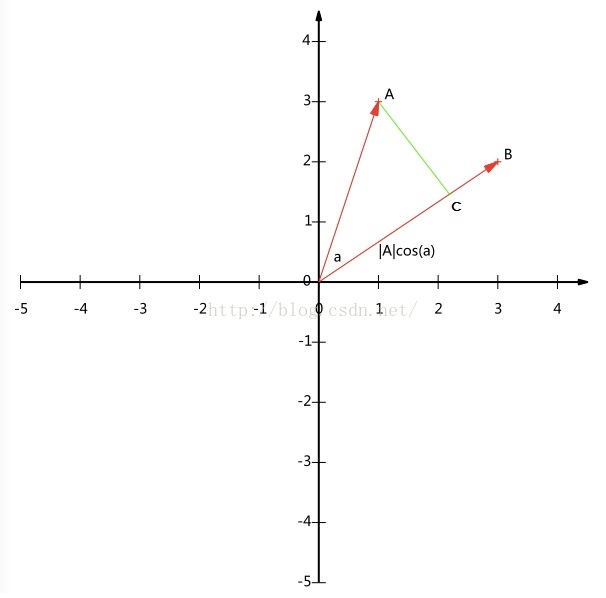
图1：内积和投影

向量的内积还有另外一种表达方式：

$A\cdot B=|A||B|cos(\alpha)$

即 A 与 B 的内积等于 A 到 B 的投影长度乘以 B 的模。 再进一步，如果我们假设 B 为单位向量，其模为1，即$|B|=1$，那么就变成了：

$A\cdot B=|A|cos(\alpha)$

也就是说，假设向量 B 为单位向量（模为1），则A与单位向量B的内积值等于A向单位向量B所在直线的投影长度，即图 1 中 OC 的长度。

基与基的坐标

如图 1 所示，众所周知，向量 B 用点坐标表示为$（3, 2）^T$。其中的 3 本质上是向量在 x 轴上的投影对应的值是3， 2是向量在 y 轴上的投影对应的值是2。也就是说我们其实隐式引入了一个定义：以x轴和y轴上正方向长度为1的向量为标准。更正式的说，向量$(x,y)^T$实际上表示向量在x轴和y轴的线性组合：

$x(1,0)^T+y(0,1)^T$

不难证明所有二维向量都可以用这样的线性组合来表示。那么，此处$(1,0)^T$和$(0,1)^T$叫做二维空间中的一组基。

图2：什么是基

所以，要准确描述向量，首先要确定一组基，然后给出在基所在的各个直线上的投影值，这些投影值就是当前基所确定的坐标。只不过我们经常省略第一步，而默认以$(1,0^T)$和$(0,1)^T$为基。我们之所以默认选择$(1,0^T)$和$(0,1)^T$为基，因为它们分别是x和y轴正方向上的单位向量，因此就使得二维平面上点坐标和向量一一对应，非常方便。但实际上任何两个线性无关的二维向量都可以成为一组基，所谓线性无关在二维平面内可以直观认为是两个不在一条直线上的向量。
例如，$(1,1)^T$和$(-1,1)^T$也可以成为一组基。一般来说，我们希望基的模是1，因为从上节中内积的意义可以看到，如果基的模是1，那么就可以方便的用向量点乘基（坐标与基的内积）而直接获得其在基上的坐标了！实际上，对应任何一个向量我们总可以找到其同方向上模为1的向量，只要让两个分量分别除以模就好了。例如，上面的基$(1,1)^T$和$(-1,1)^T$可以变为$(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})^T$和$(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})^T$。

现在，我们想获得$(3,2)^T$在新基上的坐标，即在两个方向上的投影矢量值，那么根据内积的几何意义，我们只要分别计算$(3,2)^T$和两个基的内积，不难得到新的坐标为$(\frac{5}{\sqrt{2}},-\frac{1}{\sqrt{2}})^T$。图3给出了新的基以及$(3,2)^T$在新基上坐标值的示意图（建议左上斜四十五度看）：

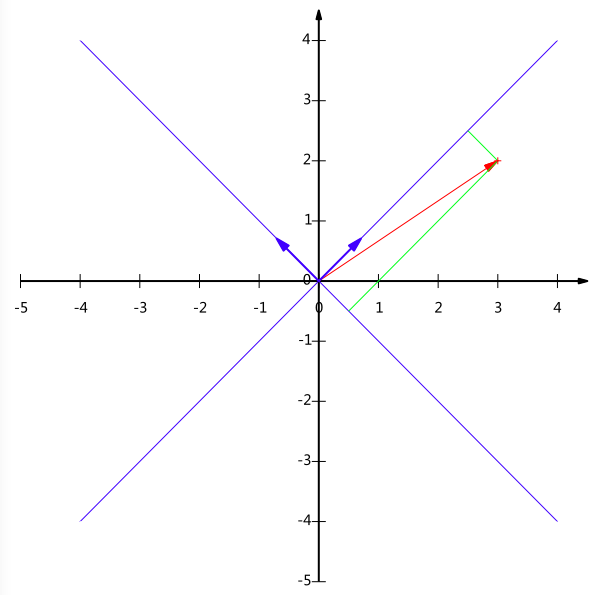
图3：基变换

另外这里要注意的是，我们列举的例子中基是正交的（即内积为0，或直观说相互垂直），但可以成为一组基的唯一要求就是线性无关，非正交的基也是可以的。不过因为正交基有较好的性质，所以一般使用的基都是正交的。（如果新基是正交矩阵，这里即从旧基到新基的过渡矩阵为正交矩阵$C$，那么非常方便的可以求得在新基下的坐标 $\eta = C^{-1}\xi = C^T\xi$，正交方阵是欧氏空间中标准正交基到标准正交基的过渡矩阵。）

基变换的矩阵表示

下面我们找一种简便的方式来表示基变换。还是拿上面的例子，想一下，将$(3,2)^T$变换为新基上的坐标，就是用$(3,2)^T$与第一个基做内积运算，作为第一个新的坐标分量，然后用$(3,2)^T$与第二个基做内积运算，作为第二个新坐标的分量。实际上，我们可以用矩阵相乘的形式简洁的表示这个变换：

$\begin{pmatrix} 1/\sqrt{2} & -1/\sqrt{2} \\ 1/\sqrt{2} & 1/\sqrt{2} \end{pmatrix}^T \begin{pmatrix} 3 \\ 2 \end{pmatrix}= \begin{pmatrix} 5/\sqrt{2} \\ -1/\sqrt{2} \end{pmatrix}$

太漂亮了！其中矩阵的两列分别为两个基，其转置乘以原向量，其结果刚好为新基的坐标。可以稍微推广一下，如果我们有m个二维向量，只要将二维向量按列排成一个两行m列矩阵，然后用“基矩阵的转置（其实是过渡矩阵的逆）”乘以这个矩阵，就得到了所有这些向量在新基下的值。例如 (1,