本附录中,我们将以向量与点为基石来构建出更为复杂的几何图形。
1.射线、直线以及线段
一条直线可以用线上一点以及与此线平行的向量u来表示,所以,此直线的向量直线方程(vector line equation)为:
其中t∈R

通过赋予t不同的值,我们就能获得直线上的不同的点。
如果将t限制为非负数,那么这个向量直线方程的图像就变为射线
线段:假设通过端点来定义一条线段,那么将
,那么原向量直线方程变成:
然后t被限定在[0,1]的范围之内。
2.平行四边形
根据向量直线方向的思想:设q为一点,且u和v是两个非平行向量,可以得到平行四边形方程:
其中s,t∈[0,1]
如果限制为0~1的话,向量u/v的长度刚好就是边长

如果u和v相互平行,那么p方程可以转换成直线方程,变成单自由度方程
单自由度(one degree of freedom)方程,双自由度方程。要想获得像平行四边形这样的2D几何形状,必须采取双自由度方程。
3.三角形
三角形的向量方程和平行四边形的差不多,就是进一步限制了s,t的范围:
其中s≥0,t≥0,s+t≤1
注意,三角形就是平行四边形的一半,所以≤1就能很好的理解
如果给出三角形的三个点,我们能将uv换成对应的向量:
我们就得到了重心坐标:,或者把1-s-t换成r,重心坐标表示了三角形的三个顶点的加权平均值。
4.平面
我们可以把一个平面视为一张无限薄、无限宽以及无限长的“三无”纸。一个平面可以用一个向量(n不一定具有单位长度)与平面内一点
来表示。
一个平面可以将空间划分为正半空间(positive half-space)与负半空间(negative half-space)。正半空间也为平面前侧的空间,也就是平面法向量指向的一侧。

平面内的点p与p0的连线一定正交于n,所以我们就得到了平面方程(plane equation):
因为在描述一个特定平面的时候,法线n与平面内的点p0都是确定下来的,所以平面方程可以改写为:
其中:
如果且
,那么平面方程就可以写作:
⭐
如果平面法向量n为单位长度,那么d表示的就是从坐标新原点至此平面的最短“有符号”(或"有向")距离。-- 有符号距离意思是θ角度若大于90°,则为负

总结:
平面法向量n=(a,b,c),平面到原点的距离为||d||,那么平面方程:
ax+by+cz+d=0
d具体取正或负取决于平面法线的朝向,如果平面法线朝外(站在原点来看),那么d取正
d = -n·p_0
①DirectX数学库中平面的表示:
存储法向量n与常量d是一件很容易的事,[或者说存储平面方程中abcd四个参数的量很容易,]我们可以把它们表示为。因此我们可以用XMVECTOR类型来存储这个浮点数值四元组。
DirectX数学库也提供了XMVECTOR类型的重载用于表示平面。
②空间点与平面的位置关系:
回顾平面方程:
判断空间点与平面的位置关系:方程表示的是两个向量(平面法向量和平面内某向量)的夹角θ的余弦值cosθ,因为正交所以=0。如果左式>0,代表cosθ>0,说明此时点p0位于平面的前侧空间。同理,左式<0,说明p0位于平面的后侧空间。
DirectX数学库提供函数专门计算特定点的:
XMVECTOR XMPlaneDotCoord( // 返回每个坐标分量都存有n·p+d计算结果的XMVECTOR
XMVECTOR P, // (a,b,c,d)表示的平面
XMVECTOR V // (x,y,z,w=1)来表示的点
);
// n·p+d=ax+by+cz+d
// 使用:判断平面与点的关系:
float x = XMVectorGetX(XMPlaneDotCoord(p, v));
if(x约等于0.f)
else if(x>0)
else if(x<0)还有类似的函数计算:返回平面法向量与指定的3D向量的点积:
XMVECTOR XMPlaneDotNormal(XMVECTOR Plane, XMVECTOR Vec);③构建平面:
除了直接指定平面系数(n,d)=(a,b,c,d)之外,还有两种方式来计算这些系数:
- 给出法线n与平面内一已知点
,就能解出d:
// 平面内一点与法线构建对应的平面(n,d)
XMVECTOR XMPlaneFromPointNormal(
XMVECTOR Point,
XMVECTOR Normal
);- 指定目标平面内3个不共线的点:
XMVECTOR XMPlaneFromPoints(
XMVECTOR Point1,
XMVECTOR Point2,
XMVECTOR Point3
);④对平面进行规范化处理:
有些时候,我们可能需要对平面的法向量进行规范化处理。但是注意,d的表示也依赖于法向量n,所以对n除以||n||进行规范化处理时,d也要除以||n||。
XMVECTOR XMPlaneNormalize(XMVECTOR P);⑤对平面进行变换:
[Lengyel02]证明了:如果要对一个平面(n,d)进行某种变换,可以先将它作为一个4D向量,再令它乘以所需变换矩阵的逆转置矩阵即可。
补充知识:用变换矩阵处理以下数据(不同数据进行矩阵变换):
①点:
点直接乘上变换矩阵即可,然后w=1
②向量:
??????????????????????????????????????????????????????
在变换之前,首先得保证法向量是规范化的。
XMVECTOR XMPlaneTransform(XMVECTOR P, XMMATRIX M);示例代码:
XMMATRIX T(...); // T初始化为需要的变换矩阵
XMMTARIX invT = XMMatrixInverse(XMMatrixDeterminant(T), T);
XMMATRIX invTransposeT = XMMatrixTranspose(invT);
XMVECTOR p = (...); // 初始化平面
p = XMPlaneNormalize(p); // 确定法线是规范化的
XMVECTOR transformedPlane = XMPlaneTransform(p, &invTransposeT);⑥平面内离指定点最近的点:
假设空间点p,欲求出平面(n,d)上至点p最近的一点q。
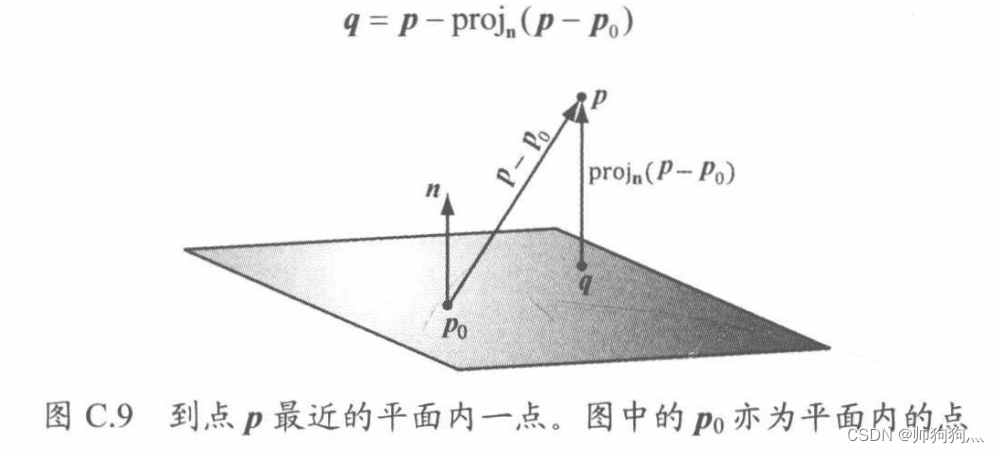
假设,因此有
所以:
⑦射线与平面的相交检测:
指定一条射线与一个平面的方程
,我们就能知道射线与平面是否相交以及相交时的交点。为此,我们要将射线代入平面方程,并解出满足此平面方程的参数t,借入根据参数求出两者的交点。
假设平面上的点也在射线上,将射线p的方程代入平面:
如果,那么射线与平面平行,方程不是无解就是无穷个解(射线在平面内)。如果t不在区间[0,∞)内,那么射线不与平面相交,但该射线所在直线与平面相交。如果t在[0,∞)内,那么射线与平面相交,就可以通过t为
的射线方程求出两者的交点。
射线与平面的相交检测可以方便地该做线段与平面的相交检测。若给出定义一条线段的两个端点p与q,那么就可以用它们来构建射线。我们就将这条射线用于相交检测。如果t∈[0,1],那么线段与平面相交,否则就不相交。
// Intersect:相交
// 该函数判断平面与线段是否相交
XMVECTOR XMPlaneIntersectLine(
XMVECTOR P,
XMVECTOR LinePoint1,
XMVECTOR LinePoint2
);
// 返回值:交点⑧反射向量:
指定一个向量I,欲求出它关于某平面法线n的反射向量。
❌: 因为n只是方向,n的大小是无关的
✔:这里我们假设n是单位向量:
I的方向是入射方向,指向反射点,如图:

⑨反射点(对称点):

⑩反射矩阵:
























 2696
2696











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








