植树造图——一杯茶，一个盘子，一个题目干4h

Prim相比于Kruskal的优势？

递归构造CBT(by FBT+CBT in recursion)

• 数组树，用递归，不要浪费时间构建完整的树
  

idea+comment

• 我选择直接从这N个树构造CBT
• way0. 递归，保证每次加入一个节点都形成CBT，难度巨大
• way1. 每次先找根，然后分成左右两个子树,用递归即可,但还要联系左右子树的区间
• way2. 补全成满二叉树，自第二上归并构造，这个容易点，接着层序遍历,忽略补上的数，但不喝题意
• 综上，只能用way1,好痛苦呀,
• 好消息是，way1的一部分可以用到way2，好像实际上，way1可以借助于way2迭代; 但无论怎么说，这个题目挺复杂的
• tuple<type1,…,type3> result=make_tuple<type1,…,type3>,return result;
• tie<type1,…,type3>=result;
• 完成:cal_loc_root_lr(),build_full_binary_tree(),build_CBT(),main()
• check-1: 完全平衡,最大N 错误
  comment1: some trifle calculation in cal_loc_root_lr

code+result

#include<iostream>
#include<vector>
#include<queue>
#include<cmath>
#include<tuple>    //fullfilled by struct
#include<algorithm>
using namespace std;

class Node{
public:
    Node *lc;
    Node *rc;
    int val;
};

//check-1
tuple<int,int> cal_loc_root_lr(vector<int> &ele,int begin,int end){
    //进入条件为end-begin>=0,len>=1,不用考虑len=0
    int len=end-begin+1;
    int h=log(len)/log(2)+1;
    int lr;    //lr=0表示最底层左边非空，lr=1表示最底层右边非空
    int loc_root;
    tuple<int,int> result;
    //需要区分~h=1~ len=1的情形
    if(h==1){
        lr=0;
        loc_root=begin;
    }
    else{
        if(len<=begin+3*pow(2,h-2)-2){    
            lr=0;
            loc_root=end-pow(2,h-2)+1;
        }
        else {
            lr=1;
            loc_root=begin+pow(2,h-1)-1;
        }
    }
    result=make_tuple(lr,loc_root);
    return result;
}

//check-1
Node* build_full_binary_tree(vector<int> &ele,int begin,int end){
    if(end-begin<0)
        return NULL;
    int mid=(begin+end)/2;
    Node *root=new Node;
    root->val=ele[mid];
    if(end-begin>0){
        root->lc=build_full_binary_tree(ele,begin,mid-1);
        root->rc=build_full_binary_tree(ele,mid+1,end);
    }
    else{
        root->lc=NULL;    
        root->rc=NULL;
    }
    return root;
}

//check-1
Node* build_CBT(vector<int> &ele,int begin,int end){
    //终止条件
    if(end-begin<0)
        return NULL;
    //迭代过程(end-begin>=0)
    int lr,loc_root;
    tie(lr,loc_root)=cal_loc_root_lr(ele,begin,end);
    // cout<<"begin="<<begin<<",end="<<end<<",loc_root"<<loc_root<<endl;
    Node *root=new Node;
    root->val=ele[loc_root];
    if(lr==0){
        root->lc=build_CBT(ele,begin,loc_root-1);
        root->rc=build_full_binary_tree(ele,loc_root+1,end);
    }
    else{
        root->lc=build_full_binary_tree(ele,begin,loc_root-1);
        root->rc=build_CBT(ele,loc_root+1,end);
    }
    return root;
}

//check-1
int main(){
    int N;    cin>>N;
    vector<int> ele(N);
    for(int i=0;i<N;i++)
        cin>>ele[i];
    sort(ele.begin(),ele.end());
    Node *root=build_CBT(ele,0,ele.size()-1);
    //perform level-order traverse
    queue<Node*> nqueue;
    nqueue.push(root);
    int sign=0;
    while(!nqueue.empty()){
        Node *tem=nqueue.front();
        if(sign==0){
            cout<<tem->val;
            sign=1;
        }
        else cout<<" "<<tem->val;
        if(tem->lc!=NULL)    nqueue.push(tem->lc);
        if(tem->rc!=NULL)    nqueue.push(tem->rc);
        nqueue.pop();
    }
    return 0;
}

Exp++

1. class Node{ xxx };is utilized to replace struct, assigning of which is Node * root=new Node[size]
2. function in C++ can return multiple values as follows:

//返回值
tuple<type1,...,type3> result=make_tuple<x1(type1),...,x3(type3)>,return result;
//接收值
tie<x1(type1),...,x2(type3)>=result;

3. Depending on multiple sub-function with certain effect indicated by note to standardize main program,improving readability meanwhile for debugging.
4. 迭代过程中的计算要细心

File Transfer——伪装成青铜的王者

• 难点:1. 类定义(不会，还是用结构体); 2. 输入处理，

//judge connectivity of graph
//analogy in realistic problem
//GNode can be expressed as both class and graph matrix, the former is adopted
//exp1: the first step is combing relations between target functions
//que1: 如何对一个含有vector成员的类(的对象)进行初始化
//que2: 可以用cin判断读入的是否为空吗?—— getline(cin,),如何读取

#include<iostream>
#include<vector>    //standardization of array
#include<stack>    //for DFS of graph nodes
using namespace std;

struct GEdge{
    int index;
    GEdge * next;
};

struct GNode{
    int val;
    GEdge* firstedge;
};

//含vector成员类对象的初始化
struct Graph{
    int Nv;
    GNode* GNodeList;
};    //无向图

//链表尾插入节点待处理
bool c1_to_c2(Graph* G,int c1,int c2){
    if(c1==c2)    return false;
    GEdge* ec1=G->GNodeList[c1].firstedge;
    while(ec1->next!=NULL){
        if(ec1->index==c2)    return false;    //已建立连接，对称，故直接返回
        else ec1=ec1->next;
    }
    //采用头插法
    GEdge* new_ec2=new GEdge;
    new_ec2->index=c2;
    new_ec2->next=ec1;
    G->GNodeList[c1].firstedge=new_ec2;
    return true;
}
void connect(Graph* G,int c1,int c2){
    if(c1_to_c2(G,c1,c2)==false){    //c1指向c2
        return ;
    }
    c1_to_c2(G,c2,c1);    //c2指向c1
    return ;
}

//DFS from GNode c1
void DFS(Graph* G,vector<int> &visit,int c1){    //引用变量才能修改，vector好像是指针，不用左引用&
    stack<GNode> nstack;
    nstack.push(G->GNodeList[c1]);
    while(!nstack.empty()){
        GEdge* tem=nstack.top().firstedge;
        int sign=0;
        while(tem!=NULL){
            if(visit[tem->index]==0){
                visit[tem->index]=1;
                nstack.push(G->GNodeList[tem->index]);
                sign=1;
            }
            else tem=tem->next;
        }
        if(sign==0)    nstack.pop();
    }
    return ;
}

//perform DFS from c1
//另一种栈式遍历，不用visit数组背诵,好像还是要visit数组
void Check(Graph* G,int c1,int c2){
    vector<int> visit(G->Nv,0);
    if(c1==c2){
        cout<<"no"<<endl;
        return ;
    }
    stack<GNode> nstack;
    visit[c1]=1;
    nstack.push(G->GNodeList[c1]);
    while(!nstack.empty()){
        GEdge* tem=nstack.top().firstedge;
        while(tem!=NULL){
            if(tem->index==c2){
                cout<<"yes"<<endl;
                return ;
            }
            if(visit[tem->index]==0){
                visit[tem->index]=1;
                nstack.push(G->GNodeList[tem->index]);
            }
            tem=tem->next;
        }
    }
    cout<<"no"<<endl;
    return ;
}

//DFS from each unvisited GNode
void Isolation(Graph* G){
    vector<int> visit(G->Nv,0);
    int cnt=0;
    for(int i=0;i<G->Nv;i++){
        if(visit[i]==0){
            DFS(G,visit,i);
            cnt++;
        }
    }
    cout<<"There are "<<cnt<<" components."<<endl;
}

//按行处理
int main(){
    int N;    cin>>N;
    Graph* G=new Graph;
    G->Nv=N;
    G->GNodeList=new GNode[N];
    for(int i=0;i<N;i++){
        G->GNodeList[i].val=i;
        G->GNodeList[i].firstedge=NULL;
    }
    string str;
    char symbol;    int c1,c2;
    int cnt=0;
    //无语的字符串读取
    while(getline(cin,str)){
        cnt++;
        cout<<str<<endl;
        if(str.empty()){
            break;
        }
        symbol=str[0];
        if(symbol=='S')
            Isolation(G);
        else {
            sscanf(str.c_str(),"%c %d %d",&symbol,&c1,&c2);
            if(symbol=='C')
                Check(G,c1,c2);
            else c1_to_c2(G,c1,c2);
        }
    }
    cout<<"there are "<<cnt<<" lines all together"<<endl;
    return 0;
}

输入处理

每次这种按行读取都要爆炸

特点

1. 按行读取，要用getline(cin,str);
2. 不同行的处理方式不同，因此不能scanf(“%d %c”,&x1,&c1);
3. cin>>N;只会按N的类型读取一个对应的变量，直到空格或换行前，但不会读取这个空格（“\ “）或换行符（”\n”）

cin读取数据是从第一个非空白字符开始到下一个空白字符结束;
如果我在第一次输入时，利用空格隔开两个字符串，那么cin在第一次取的时候，只会读取前一个字符串，到空格结束，此时缓冲区还保留着前面输入的第二个字符串，那么第二次cin就会直接从缓冲区取残留数据，而不会请求输入。
cin、cin.get()、cin.getline()、getline()的区别

4. 读取"\n"：a) char str1[50]; gets(str1); b)string str1; getline(cin,str1);
   a)在.c可以用，在.cpp不能用，C++11标准已移除；
   
5. scanf()从光标位置读取，因此光标在换行符处getline(cin,litter)掉换行符；cin>>自动从下一个非空格非"\n"读取，故不用getline(cin,str1)读掉换行符；
6. scanf()并不是读到换行符停止，而是遇到空白字符（空格、制表符、换行符等），在仅仅读取一行时有效；
   读取一整行再处理，要跟一个getline(cin,rubbish);读掉"\n"；或者getline(cin,str1);+sscanf(str1.c_str(),"%d %s",&x1,str1)

• 字符处理部分如下：

    int N;    cin>>N;
    string str;
    char symbol;    int c1,c2;
    int cnt=0;
    //无语的字符串读取
    while(getline(cin,str)){
        cnt++;
        cout<<str<<endl;
        if(str.empty()){
            break;
        }
        symbol=str[0];
        if(symbol=='S')
            Isolation(G);
        else {
            sscanf(str.c_str(),"%c %d %d",&symbol,&c1,&c2);
            if(symbol=='C')	Check(G,c1,c2);
            else c1_to_c2(G,c1,c2);
        }
    }
    cout<<"there are "<<cnt<<" lines all together"<<endl;

结果

说明只读了个空行，然后跳出；
推测: cin>>N读了5赋值给N后，还有"\n"未读取，getline()跟着读取后赋值给str，遂break;
果然是这样——在cin>>N后，跟着一个getline(cin,str);读掉空行后结果如下：

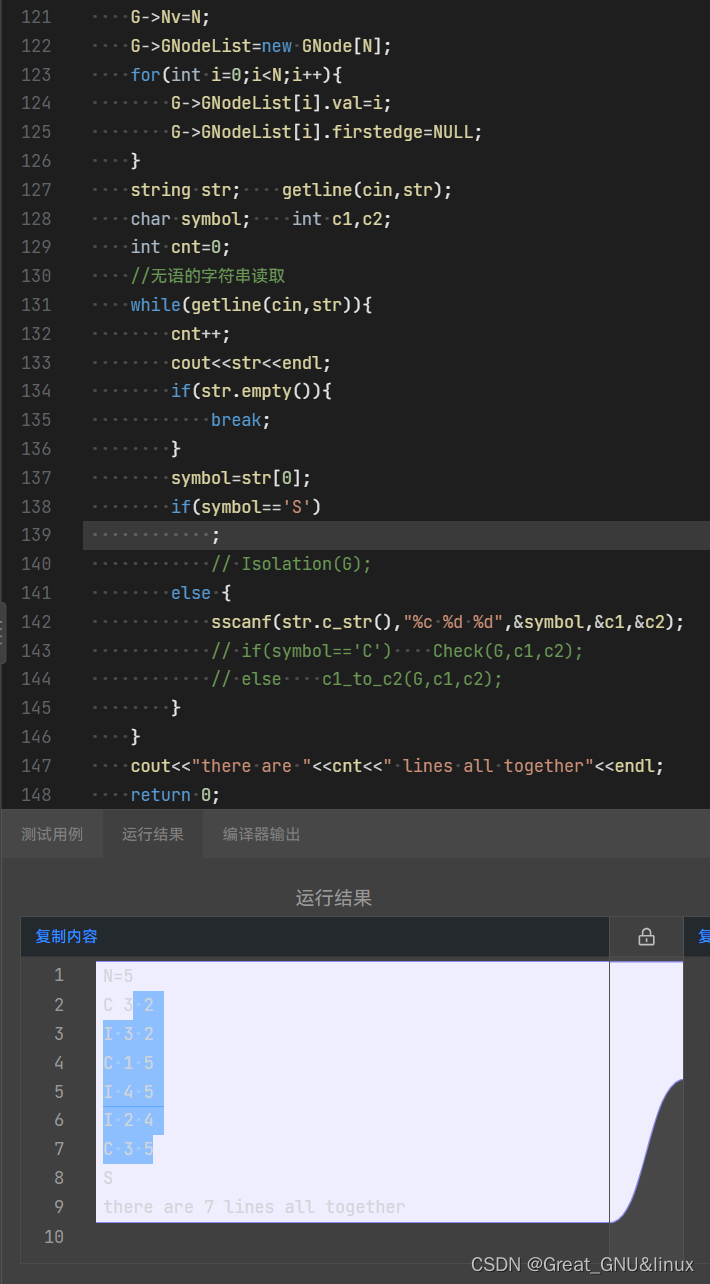
段错误

控制变量法(分别Note掉line 140,143,144)，用简单的例子测试，发现connect函数有问题(而且connect打成c1_to_c2了~~)
分析如下:

• 序号为i的node在GNode中的位置为i-1
• 修改1:N+1个节点,查联通分量从1开始; 修改2:i在GNodelist[i]中坐标为i-1,但index和val仍为i;
• 采用修改1:

更新(头插法不用遍历)如下:

//judge connectivity of graph
//analogy in realistic problem
//GNode can be expressed as both class and graph matrix, the former is adopted
//exp1: the first step is combing relations between target functions
//que1: 如何对一个含有vector成员的类(的对象)进行初始化
//que2: 可以用cin判断读入的是否为空吗?—— getline(cin,),如何读取
//err1: 超时>>while无限循环>>迭代后未更新变量
//err2: 段错误>>访问了不能访问的指针(变量)
//check2:

#include<iostream>
#include<vector>    //standardization of array
#include<stack>    //for DFS of graph nodes
using namespace std;

struct GEdge{
    int index;
    GEdge * next;
};

struct GNode{
    int val;
    GEdge* firstedge;
};

//含vector成员类对象的初始化
struct Graph{
    int Nv;
    GNode* GNodeList;
};    //无向图

//链表尾插入节点待处理, check:1
void c1_to_c2(Graph* G,int c1,int c2){
    if(c1==c2)    return ;
    GEdge* ec1=G->GNodeList[c1].firstedge;
    //用头插法不用遍历到邻接链表尾
    // while(ec1!=NULL){
    //     if(ec1->index==c2)    return false;    //已建立连接，对称，故直接返回
    //     else ec1=ec1->next;
    // }
    //采用头插法
    GEdge* new_ec2=new GEdge;
    new_ec2->index=c2;
    new_ec2->next=ec1;
    G->GNodeList[c1].firstedge=new_ec2;
    return ;
}

void connect(Graph* G,int c1,int c2){
    c1_to_c2(G,c1,c2);    //c1指向c2
    c1_to_c2(G,c2,c1);    //c2指向c1
    return ;
}

//perform DFS from c1
//另一种栈式遍历，不用visit数组背诵,好像还是要visit数组
void Check(Graph* G,int c1,int c2){
    vector<int> visit(G->Nv+1,0);
    if(c1==c2){
        cout<<"yes"<<endl;
        return ;
    }
    stack<GNode> nstack;
    visit[c1]=1;
    nstack.push(G->GNodeList[c1]);
    while(!nstack.empty()){
        GEdge* tem=nstack.top().firstedge;
        nstack.pop();
        while(tem!=NULL){
            if(tem->index==c2){
                cout<<"yes"<<endl;
                return ;
            }
            if(visit[tem->index]==0){
                visit[tem->index]=1;
                nstack.push(G->GNodeList[tem->index]);
            }
            tem=tem->next;
        }
    }
    cout<<"no"<<endl;
    return ;
}


//DFS from GNode c1; check:1
void DFS(Graph* G,vector<int> &visit,int c1){    //引用变量才能修改，vector好像是指针，不用左引用&
    stack<GNode> nstack;
    nstack.push(G->GNodeList[c1]);
    while(!nstack.empty()){
        GEdge* tem=nstack.top().firstedge;
        int sign=0;
        while(tem!=NULL){
            if(visit[tem->index]==0){
                visit[tem->index]=1;
                nstack.push(G->GNodeList[tem->index]);
                sign=1;
                break;
            }
            else tem=tem->next;
        }
        if(sign==0)    nstack.pop();
    }
    return ;
}

//DFS from each unvisited GNode
void Isolation(Graph* G){
    vector<int> visit(G->Nv+1,0);
    int cnt=0;
    for(int i=1;i<=G->Nv;i++){
        if(visit[i]==0){
            DFS(G,visit,i);
            cnt++;
        }
    }
    if(cnt==1)    cout<<"The network is connected.";
    else cout<<"There are "<<cnt<<" components."<<endl;
    return ;
}

//按行处理
int main(){
    int N;    cin>>N;
    // cout<<"N="<<N<<endl;
    Graph* G=new Graph;
    G->Nv=N;
    G->GNodeList=new GNode[N+1];
    //序号为i的node在GNode中的位置为i-1
    //修改1:N+1个节点,查联通分量从1开始; 修改2:i在GNodelist[i]中坐标为i-1,但index和val仍为i;
    //采用修改1:
    for(int i=1;i<=N;i++){
        G->GNodeList[i].val=i;
        G->GNodeList[i].firstedge=NULL;
    }
    string str;    getline(cin,str);
    char symbol;    int c1,c2;
    int cnt=0;
    //无语的字符串读取
    while(getline(cin,str)){
        cnt++;
        // cout<<str<<endl;
        if(str.empty()){
            break;
        }
        symbol=str[0];
        if(symbol=='S')
            Isolation(G);
        else {
            sscanf(str.c_str(),"%c %d %d",&symbol,&c1,&c2);
            if(symbol=='C')    Check(G,c1,c2);
            else    connect(G,c1,c2);
        }
    }
    // cout<<"there are "<<cnt<<" lines all together"<<endl;
    return 0;
}

结果如下:

Exp++

• 这么简单的题目，浪费好多时间

Push

1. cin>>variable从第一个非空白符读到下一个"\ “/”\n"，getline(cin,str)会读完以"\n"结尾的一整行，共用<iostream>头文件
2. 字符串->其他类型用stox（in ）,其他类型转char *用sprintf()，"="转为string

#include<iostream>
using namespace std;

int main(){
    string tem="1245";
    int b=stoi(tem)-10;
    char str1[10];
    sprintf(str1,"%d",b+20);
    string s1=str1;
    string flos="12.3";
    float h=stof(flos);
    cout<<b<<endl;
    cout<<str1;
    cout<<s1<<endl;
    cout<<h<<endl;
}

3. 节点的链接链表的插入宜采用头插法（不用遍历到Tail+不用单独处理头指针是否为NULL）
4. 段错误>>数组越界>>数组序号==真实序号-1，超时>>while无限循环>>迭代条件未更新
5. 试用类表示节点，并初始化(+其中的vector数组)
6. 针对测试点6，并查集能被用到这个题目，整道题目都在梦游~~，试用Union-Find set解答此题目

Pop

1. 两种方式的栈式先序遍历（for looking for 连通分量in 无向图）

• 如何找有向图的强连通分量——栈式(用array实现)DFS，找到在栈中的节点为一个连通分量，标记清空，如此迭代

Union-Find Set

• 1）判断图中节点的连通性
• 2）获得无向图的连通分量
• 采用路径压缩（非根节点均指向根节点）可加速查找和连接，O(1)
• 特点：仅father[连通分支的根节点]=-1，其余指向其父节点/根节点(path compress)

int component;
vector<int>    father;

int Find_Root_Comp(int x){
    if(father[x]==-1)
        return x;
    else{
        int F=Find_Root_Comp(father[x]);
        father[x]=F;
        return F;
    }
}

void Union(int x,int y){
    int fatherx=Find_Root_Comp(x);
    int fathery=Find_Root_Comp(y);
    if(fatherx!=fathery){
        father[fatherx]=fathery;
        component--;
    }
    return ;
}

bool Check(int x,int y){
    int fatherx=Find_Root_Comp(x);
    int fathery=Find_Root_Comp(y);
    if(fatherx==fathery){
        return true;
    }
    else 
        return false;
}

priority_queue计算Huffman编码总长度

priority_queue<int,vector<int>,greater<int>> f_queue;	//升序队列
priority_queue <int,vector<int>,less<int> >q;			//降序队列，定义: priority_queue<Type, Container, Functional>

int Huff_code_sum(vector<int> f_set){
//计算最小长度和只需要f_set
//way1:构造huffman树,定义节点,按算法为每个节点赋一个string成员,构造编码
//way2:书上采用priority_queue计算huffman编码总长
//but,priority_queue的头元素=top(),queue的头元素=front()
    sort(f_set.begin(),f_set.end());
    for(auto i:f_set)
        f_queue.push(i);
    int sum=0;
    while(f_queue.size()>1){
        int x=f_queue.top();
        f_queue.pop();
        int y=f_queue.top();
        f_queue.pop();
        sum+=x+y;
        f_queue.push(x+y);
    }
    return sum;
}

如何寻找源和汇的最短路径

1. 普通的栈式DFS不保证找到根到每个节点的最短路径，只能找到图中从根节点能遍历到的所有节点。 (√)
   +optimal_path+min_len可以找到最短路径。 （√）
2. 普通的Dijkstra和Floyd可以输出最短路径长，难以输出节点；
3. 递归DFS也可以，DFS均可用剪枝减小时间复杂度；
4. BFS可以容易地输出最短路径长，但是不能找到最短路径
5. 为什么BFS不适合用递归实现？——父节点的不同子节点的递归函数不交叉，不能在同一层输出；
   或者说，什么样的结构适合用递归实现——子问题的解可以容易地拼接成原问题的解；=DP

最短路长用BFS

7.11

//用图数据结构表示，
//用BFS，队列实现的时候，给未遍历的每个节点赋一个位置数组
//也可以DFS寻找最短S和D的最短路径
//试一下可以用邻接矩阵形式的图结构，这样不必定义图节点，
//递归标记最短路径,
//~~1)多条最短路径仍需处理;~~
//2)非递归形式=回溯剪枝?

//note: 简单的例子能提供更高效的信息

#include<iostream>
#include<vector>
#include<cmath>
using namespace std;
int N,D;
vector<pair<int,int>> coord;
int min_len=1000;
vector<int> optimal_path;

bool check(int x,int y){
    if(x==0)    return (pow(coord[y].first,2)+pow(coord[y].second,2)<=pow(D+7.5,2))?true:false;
    return (pow(coord[x].first-coord[y].first,2)+pow(coord[x].second-coord[y].second,2)<=pow(D,2))?true:false;
}

//检查非根节点是否可以到岸
bool test_plausible(int x){
    if(x==0)    return    (abs(coord[x].first-50)<=D+7.5||abs(coord[x].first+50)<=D+7.5||\
       abs(coord[x].second-50)<=D+7.5||abs(coord[x].second+50)<=D+7.5)?true:false;
    return (abs(coord[x].first-50)<=D||abs(coord[x].first+50)<=D||\
       abs(coord[x].second-50)<=D||abs(coord[x].second+50)<=D)?true:false;
}

//递归寻找最短路径,赋值给optimal_path
void shortest_path(int root,vector<int> &path,int depth,vector<int> &visit){
    //depth表示从根节点到root的路径的节点数目数
    //path初始化为(N+1,-1);    depth不能用引用改变，否则for循环中depth不等
    for(int i=0;i<=N;i++){
        if(i!=root&&check(root,i)&&visit[i]==0){    //i与root相连且未访问
            visit[i]=1;
            path[depth]=i;        //长度为depth+1，在后面第42行写错俩
            if(test_plausible(i)){
                //若有多条最短路径,需要单独处理,path[1]第一跳更小
                if(depth+1<min_len||((depth+1==min_len)&&\
                    ((pow(coord[path[1]].first,2)+pow(coord[path[1]].second,2))\
                    <=(pow(coord[optimal_path[1]].first,2)+pow(coord[optimal_path[1]].second,2))))){
                    optimal_path=path;
                    min_len=depth+1;
                    // cout<<"a new path="<<endl;
                    // for(int i=1;i<min_len;i++)
                    //     cout<<coord[optimal_path[i]].first<<" "<<coord[optimal_path[i]].second<<endl;
                }
                //这里可以剪枝——不用从i下探=执行shortest_path函数
                visit[i]=0;    //恢复现场;
             }
            else    shortest_path(i,path,depth+1,visit);
        }
    }
    visit[root]=0;    //恢复现场
    return ;
}

int main(){
    //tackle with input 
    cin>>N>>D;
    coord.assign(N+1,make_pair(0,0));
    for(int i=1;i<=N;i++)
        cin>>coord[i].first>>coord[i].second;

    // //define plausible array
    // vector<bool> plausible(N+1,0);
    // if(D>=42.5)    plausible[0]=true;
    // else     plausible[0]=false;
    // for(int i=1;i<=N;i++)
    //     plausible[i]=test_plausible(i);

    //perform dfs to search for shortest path
    vector<int> path(N+1,-1);    int depth=0;     //熟知,size+array可以表示一个栈
    vector<int> visit(N+1,0);
    visit[0]=1;        //将根节点加入队列
    path[depth]=0;
    if(test_plausible(0)){
        optimal_path=path;
        min_len=1;
    }
    else{
        shortest_path(0,path,depth+1,visit);    //保持形式一致性
    }
    if(min_len==1000){
        cout<<0<<endl;
        return 0;
    }
    cout<<min_len<<endl;
    for(int i=1;i<min_len;i++){                //根节点不用输出
        if(path[i]!=-1)
            cout<<coord[optimal_path[i]].first<<" "<<coord[optimal_path[i]].second<<endl;
        else 
            break;
    }
    return 0;
}

Exp++

1. 图结构未必要定义图节点——1）图的邻接表；2）手动判断连接关系(check(x,y))；
   同样，栈=array+size（to search for top）
2. 最短路径可用递归+剪枝——用DFS的栈式遍历(+visit)；用array path+int size保存路径上的节点；optimal_path+min_len保存路径上的点

伪代码
stack.push(root)
while(!stack.empty()){
tem=stack.top()
sign=0;
for(auto i: tem.neighbour()){
if(visit[i]==0){
visit[i]=1;
path[depth++]=i;
if(it is destination)
compare and save optimal_path& min_len;
else{
stack.push(i);
sign=1;
break;
}}}
if(sign==0){ //恢复现场
visit[i]=0;
depth–;
stack.pop();
}}

3. 调试trick++：1）简单的例子能提供更高效的反馈；2）把自己的输出和标准输出拼接作为新的输入

默写key path(自带Torpo sort)

reading

1. if 成环，输出Impossible——可用拓扑排序，成环<=>不存在拓扑排序
2. else ,output AOE=最长关键路径
3. 执行书上的算法，输出关键路径长，和关键路径，2在1的过程中进行

#include<iostream>
#include<vector>
#include<queue>
using namespace std;

void AOE(vector<int> S,vector<int> E,vector<int> L,int N){
    vector<int> in_degree(N);
    vector<int> earliest_time(N,-1);
    int earliest_comletion_time=0;
    
    for(int i=0;i<S.size();i++)
        in_degree[E[i]]++;
    queue<int> zero_point;
    int out_num=0;
    for(int i=0;i<N;i++){
        if(in_degree[i]==0){
            earliest_time[i]=0;
            zero_point.push(i);
            out_num++;
        }
    }
    while(!zero_point.empty()){
        int tem=zero_point.front();
        for(int i=0;i<S.size();i++){    //S.size()==M,遍历边
            if(S[i]==tem){
                //更新tem出发的终点的完成时间
                if(earliest_time[E[i]]==-1||earliest_time[E[i]]<earliest_time[tem]+L[i])
                    earliest_time[E[i]]=earliest_time[tem]+L[i];    
                //更新tem出发的终点的度数，
                in_degree[E[i]]--;    
                //若度数为0，更新全局最早完成时间，并入点
                if(in_degree[E[i]]==0){
                    if(earliest_comletion_time<earliest_time[E[i]])
                        earliest_comletion_time=earliest_time[E[i]];
                    zero_point.push(E[i]);
                    out_num++;
                }
            }
        }
        zero_point.pop();
    }
    if(out_num<N)
        cout<<"Impossible"<<endl;
    else
        cout<<earliest_comletion_time<<endl;
    return ;
}

int main(){
    int N,M;    cin>>N>>M;
    vector<int> S(M),E(M),L(M);
    for(int i=0;i<M;i++)
        cin>>S[i]>>E[i]>>L[i];
    AOE(S,E,L,N);
    return 0;
}

Exp++

1. 如何输出关键路径？——最短路径可以比较获得，

    Solution
    1. 先从前往后找出每个点的最早完成时间，
    2. 再反向torpo sort定出每个点的最晚完成时间，
    3. e[i]=l[i]的点在关键路径上，自后往前，每次找前一个e[i]=l[i]的点，连成关键路径，O(N^2)
   

7-21 Counting Leaves

1. 胶水，回顾了queue栈式遍历，用于记录深度by map；count leaf_num for each layer；
   

//note:如何避免自定义变量重名?

#include<iostream>
#include<vector>
#include<map>
#include<queue>
using namespace std;

int main(){
    string str;
    int N;    cin>>N;
    while(N!=0){
        int M;    cin>>M;    getline(cin,str);
        map<int,int>    depth_of_node;    //store depth for node
        map<int,vector<int>>    child_of_node;    //store children_id for each node
        //read child_of_node
        for(int i=0;i<M;i++){
            int fath;    cin>>fath;
            int child_num;    cin>>child_num;
            vector<int> child(child_num);
            for(int i=0;i<child_num;i++)
                cin>>child[i];
            getline(cin,str);
            child_of_node.insert(make_pair(fath,child));
        }
        //calculate depth_of_node by queue
        int max_depth=1;
        depth_of_node.insert(make_pair(1,1));
        queue<int> trav;
        trav.push(1);
        while(!trav.empty()){
            int tem=trav.front();
            trav.pop();    //维护迭代条件
            for(auto i:child_of_node[tem]){
                max_depth=((depth_of_node[tem]+1)>max_depth)?(depth_of_node[tem]+1):max_depth;
                depth_of_node.insert(make_pair(i,depth_of_node[tem]+1));    //计算深度:depth[child]=depth[tem]+1;
                trav.push(i);                                     //层序遍历迭代
            }
        }
        vector<int> leaf_num(max_depth+1,0);    //store leafnum for each layer; 假设根节点深度为1
        //count for each layer;
        for(auto i:depth_of_node){
            int node_id=i.first;    //node's id
            int node_depth=i.second;
            if(child_of_node[node_id].size()==0)    //为叶节点
                leaf_num[node_depth]++;
        }
        int sign=0;
        for(int i=1;i<leaf_num.size();i++){
            if(sign==0)    sign=1;
            else    cout<<" ";
            cout<<leaf_num[i];
        }
        cout<<endl;
        cin>>N;
    }
}

打卡:

B+树

最大流(抄的模板)

1. 初始化可行轨道，如f(e)=0，
   
2. 回溯(bfs记录父节点)找可增载轨道，更新f(e)，
   
3. 直到没有可增载轨道，输出此时的最大流Val(f)
   

Code Reading

传统的最大流算法如下：

1. BFS用parent数组记录，同时可以找到一条从converge到source的路径，即找可增载轨道
2. 找可增载轨道后，从尾到前遍历，记录最大可增值量，之后更新路径上的最大流值，与val(f)

这个相当于传统的改进

1. 初始默认f(e)=0，故找到可行的轨道后，可增载量=这条轨道上的最大流即为最小的管道，
2. 这个相当于每次找到可增载轨道后，从所有轨道上删除可增载部分，并加入到val(f)中，下一次迭代又相当于f(e’)=0，故可行
   但可增载量的计算和可增载轨道的寻找，并不能理解

//最大流问题
// C++ program for implementation of Ford Fulkerson algorithm
#include <iostream>
#include <limits.h>
#include <string.h>
#include <cstdio>
#include <queue>
#include <map>
#include<vector>
using namespace std; 
 
/* Returns true if there is a path from source 's' to sink 't' in
  residual graph. Also fills parent[] to store the path */
bool bfs(vector<vector<int>> rGraph,int V, int s, int t, int parent[])
{
    // Create a visited array and mark all vertices as not visited
    bool visited[V];
    memset(visited, 0, sizeof(visited));
 
    // Create a queue, enqueue source vertex and mark source vertex as visited
    queue<int> q;
    q.push(s);
    visited[s] = true;
    parent[s] = -1;
 
    // Standard BFS Loop
    int u;
    while (!q.empty())
    {
        // edge: u -> v
        u = q.front();  // head point u
        q.pop();
        for (int v = 0; v < V; ++v)  // tail point v
        {
            if (!visited[v] && rGraph[u][v] > 0)  // find one linked vertex
            {
                q.push(v);
                parent[v] = u;  // find pre point
                visited[v] = true;
            }
        }
    }
 
    // If we reached sink in BFS starting from source, then return true, else false
    return visited[t] == true;
}
 
// Returns the maximum flow from s to t in the given graph
int fordFulkerson(vector<vector<int>> graph,int V, int s, int t)
{
    int u, v;
    // int rGraph[V][V];
    vector<vector<int>>    rGraph(graph.size(),vector<int>(graph.size(),0));
 
    for (u = 0; u < V; ++u)
    {
        for (v = 0; v < V; ++v)
        {
            rGraph[u][v] = graph[u][v];
        }
    }
 
    int parent[V];
    int max_flow = 0;
 
    // Augment the flow while tere is path from source to sink
    while (bfs(rGraph, V, s, t, parent))
    {
        // edge: u -> v
        int path_flow = INT_MAX;
        for (v = t; v != s; v = parent[v])
        {
            // find the minimum flow
            u = parent[v];
            path_flow = min(path_flow, rGraph[u][v]);
        }
 
        // update residual capacities of the edges and reverse edges along the path
        for (v = t; v != s; v = parent[v])
        {
            u = parent[v];
            rGraph[u][v] -= path_flow;
            rGraph[v][u] += path_flow;  // assuming v->u weight is add path_flow
        }
 
        // Add path flow to overall flow
        max_flow += path_flow;
    }
 
    return max_flow;
}
 
int main()
{
    int N;    string str;
    string source,destination;    cin>>source>>destination>>N;    getline(cin,str);
    map<pair<string,string>,int>    oform;
    map<string,int>    dict;    dict.insert(make_pair(source,0));
    for(int i=0;i<N;i++){
        string si,di;    int cap;
        cin>>si>>di>>cap;    getline(cin,str);
        if(dict.find(si)==dict.end())
            dict.insert(make_pair(si,dict.size()));
        if(dict.find(di)==dict.end())
            dict.insert(make_pair(di,dict.size()));
        oform.insert(make_pair(make_pair(si,di),cap));
    }
    dict.insert(make_pair(destination,dict.size()));
    int V=dict.size();
    vector<vector<int>>    graph(V,vector<int>(V,0));
    for(auto i:oform)
        graph[dict[i.first.first]][dict[i.first.second]]=i.second;
    // cout << "the maximum flow from v0 to v5 is:" << endl;
    cout<<fordFulkerson(graph,V, 0, dict.size()-1);
    return 0;
}

source=converge，不行

Exp++

1. BFS用parent数组记录，同时可以找到一条从converge到source的路径，即找可增载轨道
2. 图的遍历要不邻接表，要不邻接矩阵，搜索求路径backtrack，求节点BDFS，最近点Dijkstra/Floyd，优先次序key path torpo sort，仅仅判断连通性+求最小生成树(Kruskal)用并查集，再了不起最大流