排序算法5——简单选择排序

简单选择排序的平均复杂度为 \(O(n^2)\), 但效率通常比相同平均复杂度的直接插入排序还要差。但由于选择排序是 内部排序，因此在内存严格受限的情况下还是可以用的。

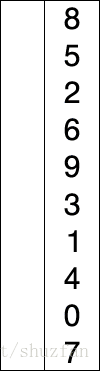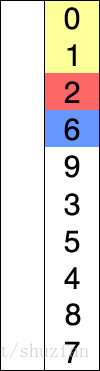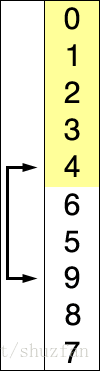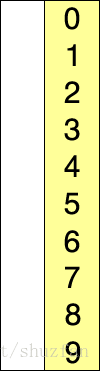
选择排序的原理很简单，如下图所示：

持续从未处理元素中找到最小值并加入到已排序列中。

黄色 表示已经排好序的子序列；蓝色表示当前处理项；红色表示当前最小值

c++实现代码如下:

#include  <iostream>
using namespace std;

// 数据交换子函数
void swap(int *data1, int *data2)
{
    int temp = *data1;
    *data1 = *data2;
    *data2 = temp;
}

// 选择排序函数，输入数组data和数据个数n
void selectSort(int data[], int n)
{
    int i, j, min_idx;

    // 外层循环，依次处理每一个元素
    for (i = 0; i < n-1; i++)
    {
        // 内层循环，从未处理元素中找到最小值位置
        min_idx = i;
        for (j = i+1; j < n; j++)
          if (data[j] < data[min_idx])
            min_idx = j;

        // 交换最小值
        swap(&data[min_idx], &data[i]);
    }
}

// 打印数组
void printarray(int data[], int n)
{
    for (int i=0; i<n; i++)
        cout << data[i] << " ";
}

int main()
{
    int data[] = {12, 34, 54, 2, 3, 12, 27, 1};
    int n = 8;

    cout << "data before shell sorting: \n";
    printarray(data, n);

    selectSort(data, n);

    cout << "\ndata after shell sorting: \n";
    printarray(data, n);

    return 0;
}

选择排序是最容易分析的，因为完整的两层循环没有跳出，循环次数为 \(\frac{n(n-1)}{2}\)。

总结

通过将上面的程序和直接插入排序相比，显然前者的循环次数要高一些，即选择排序的效率甚至还要低于直接插入排序。 但是，又可以看出前者的数据交换次数明显更少，这对于一些写比读更耗时的设备是一个优点。

参考资料：

（1） WIKI： https://en.wikipedia.org/wiki/Selection_sort