逆波兰表达式求值

一：题目

题目要求：给你一个后缀表达式，你返回该后缀表达式的值

两个题目理解问题：

Q1：什么叫中缀？

A1：中缀表达式是我们日常数学表达式中最常见的写法，运算符位于两个操作数中间。

例如：A + B 或 3 * (4 - 2)。

特点：

符合人类直觉：与自然书写习惯一致，易于阅读。

需要处理优先级和括号：运算符的优先级（如乘除高于加减）和括号会影响计算顺序。例如：3 + 4 * 2 需要先计算 4 * 2，再加 3。

可能产生歧义：复杂的表达式需要括号来明确顺序，例如 (3 + 4) * 2 与 3 + (4 * 2) 的结果不同。

缺点：
对计算机来说，不会解析一个中缀表达式来求值

Q2：什么叫后缀

A2：后缀表达式是一种运算符位于操作数之后的表达式形式。

例如：A B + 或 3 4 2 - *（对应中缀表达式 3 * (4 - 2)）。

特点：

无需括号和优先级规则：运算符的顺序直接决定了计算顺序，无需考虑优先级。

例如：3 4 2 - * 表示先计算 4 - 2，再计算 3 * 2。

适合计算机处理：可以通过简单的栈（Stack）结构高效计算。

从左到右扫描即可解析：无需回溯或复杂的语法分析。

计算机就是解析后缀表达式求值的

二：思路

计算步骤（使用栈）：

1. 从左到右扫描给我们的后缀表达式。

2. 遇到操作数时，压入栈中。

3. 遇到运算符时，弹出栈顶的两个操作数进行运算，计算得到的结果再压入栈。

4. 最终栈顶元素即为结果。

例子：

• 后缀表达式 3 4 + 5 * 对应中缀 (3 + 4) * 5。
  计算过程：

  1. 3 入栈 → 栈：[3]

  2. 4 入栈 → 栈：[3, 4]

  3. 遇到 +，弹出 4 和 3，计算 3 + 4 = 7，7 入栈 → 栈：[7]

  4. 5 入栈 → 栈：[7, 5]

  5. 遇到 *，弹出 5 和 7，计算 7 * 5 = 35，结果入栈 → 栈：[35]
     最终结果为 35。

三：代码

①：else if 法

 ②：switch case 法

三个代码理解问题：

Q1：为什么遇到符号第一个出栈的元素是右操作数？

A2：假设表达式为 3 4 +（对应中缀表达式 3 + 4）：

1. 操作数入栈顺序：

   • 3 先入栈 → 栈：[3]

   • 4 后入栈 → 栈：[3, 4]

2. 遇到操作符 +：

   • 弹出栈顶元素 4（右操作数）

   • 再弹出栈顶元素 3（左操作数）

   • 计算 3 + 4 = 7，结果入栈。

如果顺序颠倒（先弹出 3，再弹出 4），则会错误地计算为 4 + 3。虽然加法结果相同，但减法或除法会因此出错！

Q2：为什么范围for读取到的e，能进行e[ 0 ]操作？

A2：e 是字符串，不是单个字符：
题目中tokens的每个元素是string也就是字符串类型（如 "123"、"+"），且逆波兰表达式的操作符操作符字符串长度固定为1

Q3：stoi是什么函数

A3：stoi（string to integer）是C++标准库函数，接收一个字符串参数，并将其解析为整数。例如：

stoi("123") → 整数 123

stoi("-45") → 整数 -45

四：源码

①：else if 法

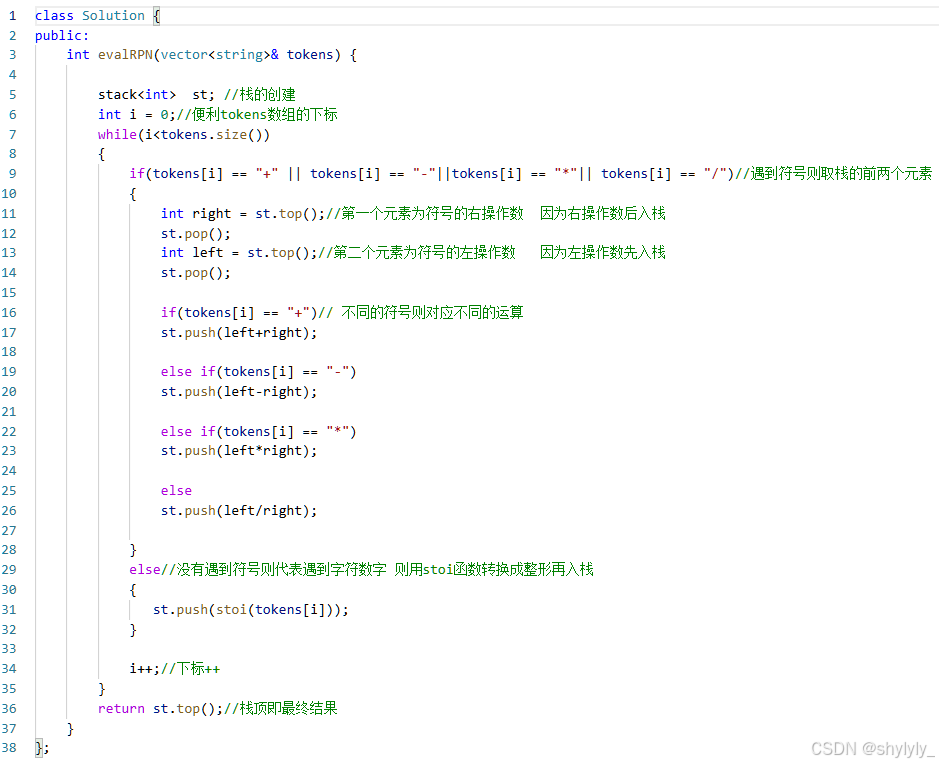
class Solution {
public:
    int evalRPN(vector<string>& tokens) {

        stack<int>  st; //栈的创建
        int i = 0;//便利tokens数组的下标
        while(i<tokens.size())
        {
            if(tokens[i] == "+" || tokens[i] == "-"||tokens[i] == "*"|| tokens[i] == "/")//遇到符号则取栈的前两个元素
            {
                int right = st.top();//第一个元素为符号的右操作数  因为右操作数后入栈
                st.pop();
                int left = st.top();//第二个元素为符号的左操作数   因为左操作数先入栈
                st.pop();

                if(tokens[i] == "+")// 不同的符号则对应不同的运算
                st.push(left+right);

                else if(tokens[i] == "-")
                st.push(left-right);

                else if(tokens[i] == "*")
                st.push(left*right);

                else
                st.push(left/right);

            }
            else//没有遇到符号则代表遇到字符数字 则用stoi函数转换成整形再入栈 
            {
               st.push(stoi(tokens[i]));
            }

            i++;//下标++
        }
        return st.top();//栈顶即最终结果
    }
};

②：switch case 法 

class Solution {
public:
    int evalRPN(vector<string>& tokens) {

        stack<int>  st; //栈的创建
       
        for(auto e : tokens)
        {
            if(e == "+" || e == "-"||e == "*"|| e == "/")//遇到符号则取栈的前两个元素
            {
                int right = st.top();//第一个元素为符号的右操作数  因为右操作数后入栈
                st.pop();
                int left = st.top();//第二个元素为符号的左操作数   因为左操作数先入栈
                st.pop();

                switch(e[0])// 不同的符号则对应不同的运算
                {
                    case '+':
                    st.push(left+right);
                    break;

                    case '-':
                    st.push(left-right);
                    break;

                    case '*':
                    st.push(left*right);
                    break;

                    case '/':
                    st.push(left/right);
                    break;
                }
            }
            else//没有遇到符号则代表遇到字符数字 则用stoi函数转换成整形再入栈 
            {
               st.push(stoi(e));
            }

        }
        return st.top();//栈顶即最终结果
    }
};