🔎大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流🔎
📝个人主页－Sonhhxg_柒的博客_CSDN博客 📃
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏 - 机器学习【ML】 自然语言处理【NLP】 深度学习【DL】
🖍foreword
✔说明⇢本人讲解主要包括Python、机器学习（ML）、深度学习（DL）、自然语言处理（NLP）等内容。
如果你对这个系列感兴趣的话，可以关注订阅哟👋
文章目录
在前两章（高级卷积网络和对象检测和图像分割）中，我们专注于有监督的计算机视觉问题，例如分类和对象检测。在本章中，我们将讨论如何在无监督神经网络的帮助下创建新图像。毕竟，知道您不需要标记数据会好得多。更具体地说，我们将讨论生成模型。
本章将涵盖以下主题：
- 生成模型的直觉和证明
- 变分自动编码器( VAE )简介
- 生成对抗网络( GAN )简介
- GAN 的类型
- 介绍艺术风格转移
生成模型的直觉和证明
到目前为止，我们已经使用神经网络作为判别模型。这仅仅意味着，给定输入数据，判别模型会将其映射到某个标签（换句话说，分类）。一个典型的例子是 MNIST 图像在 10 个数字类别中的分类，其中神经网络将输入数据特征（像素强度）映射到数字标签。我们也可以用另一种方式说：判别模型给了我们（类），给定（输入）的概率。在 MNIST 的情况下，这是给定图像像素强度时数字的概率。 
另一方面，生成模型学习类是如何分布的。你可以认为它与判别模型的作用相反。在给定某些输入特征时，它不是预测类别概率 ，而是尝试预测给定类别时输入特征的概率 -
。例如，当给定数字类时，生成模型将能够创建手写数字的图像。因为我们只有 10 个类，所以它只能生成 10 个图像。然而，我们只是用这个例子来说明这个概念。实际上，该类可以是任意值的张量，并且该模型将能够生成无限数量的具有不同特征的图像。如果您现在不明白这一点，请不要担心；出色地 查看本章中的许多示例。
在本章中，我们将用小写的p来表示概率分布，而不是我们在前几章中使用的通常的大写P。我们这样做是为了遵循在 VAE 和GAN的背景下建立的惯例。在写这本书时，我找不到使用小写字母的明确理由，但一种可能的解释是P表示事件的概率，而p表示随机变量的质量（或密度）函数的概率。
以生成方式使用神经网络的两种最流行 的方法是通过 VAE 和 GAN。在下一节中，我们将介绍 VAE。
VAE 简介
要了解 VAE，我们需要谈谈常规 自动编码器。自编码器是一种前馈神经网络，它试图重现其输入。换句话说，自动编码器的目标值（标签）等于输入数据，y i = x i，其中i是样本索引。我们可以正式地说它试图学习一个恒等函数（一个重复其输入的函数）。由于我们的标签只是输入数据，因此自动编码器是一种无监督算法。 
下图表示一个自动编码器：
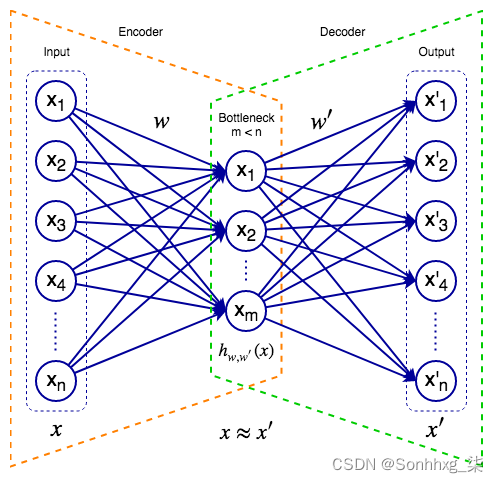
自动编码器
自编码器由输入层、隐藏层（或瓶颈层）和输出层组成。与 U-Net（第 4 章，目标检测和图像分割）类似，我们可以将自动编码器视为两个组件的虚拟组合：
- 编码器：将输入数据映射到网络的内部表示。为了简单起见，在这个例子中，编码器是一个单一的、完全连接的隐藏瓶颈层。内部状态只是它的激活向量。一般来说，编码器可以有多个隐藏层，包括卷积层。
- 解码器：尝试从网络的内部数据表示重构输入。解码器也可以具有通常反映编码器的复杂结构。当 U-Net 尝试将输入图像转换为某个其他域的目标图像（例如，分割图）时，自动编码器只是尝试重建其输入。
我们可以通过最小化损失函数来训练自编码器，这被称为重建 误差。它测量原始输入与其重建之间的距离。我们可以用通常的方式最小化它，即使用梯度下降和反向传播。根据我们使用的方法，我们可以使用均方误差( MSE ) 或二元交叉熵（例如交叉熵，但有两个类别）作为重构误差。
此时，您可能想知道自动编码器的意义何在，因为它只是重复输入。但是，我们对网络输出不感兴趣，而对它的内部数据表示（也称为潜在空间中的表示）感兴趣。潜在空间包含隐藏的数据特征，这些特征不是直接观察到的，而是由算法推断出来的。关键是瓶颈层的神经元少于输入/输出的神经元。这有两个主要原因：
- 因为网络试图从较小的特征空间重建其输入，所以它学习了数据的紧凑表示。您可以将其视为压缩（但不是无损）。
- 通过使用更少的神经元，网络被迫只学习数据中最重要的特征。为了说明这个概念，让我们看一下去噪自动编码器，我们在训练期间故意使用损坏的输入数据，但未损坏的目标数据。例如，如果我们训练去噪自动编码器来重建 MNIST 图像，我们可以通过将最大强度（白色）设置为图像的随机像素来引入噪声（如下面的屏幕截图所示）。为了最小化无噪声目标的损失，自动编码器被迫超越输入中的噪声，只学习数据的重要特征。但是，如果网络的隐藏神经元多于输入，它可能会过度拟合噪声。加上较少隐藏神经元的额外约束，它只能尝试忽略噪声。一经训练，
编码器将每个输入样本映射到潜在空间，其中潜在表示的每个属性都有一个离散值。这意味着输入样本只能具有一种潜在表示。因此，解码器只能以一种可能的方式重建输入。换句话说，我们可以生成一个输入样本的单个重建。但我们不想要这个。相反，我们希望生成与原始图像不同的新图像。VAE 是该任务的一种可能解决方案。
VAE 可以用概率术语描述潜在表示。也就是说，不是离散值，而是每个潜在属性的概率分布，使潜在空间连续。这使得随机采样和插值更容易。让我们用一个例子来说明这一点。想象一下，我们正在尝试对车辆的图像进行编码，而我们的潜在表示是一个向量z，具有n 个元素（瓶颈层中有n 个神经元）。每个元素代表一个车辆属性，例如长度、高度和宽度（如下图所示）。
假设平均车辆长度为四米。VAE 可以将此属性解码为平均值为 4 的正态分布，而不是固定值（其他属性也是如此）。然后，解码器可以选择从潜在变量的分布范围内对其进行采样。例如，与输入相比，它可以重建更长更低的车辆。通过这样做，VAE 可以生成无限数量的输入修改版本：
让我们形式化一下：
-
编码器的目标是逼近真实概率分布
，其中z是潜在空间表示。然而，它是通过从各种样本的条件概率分布中间接推断出来的
，其中x是输入数据。换句话说，编码器尝试学习z的概率分布，给定输入数据x 。我们将用 表示编码器的近似值，其中φ是网络的权重。编码器输出是z的可能值上的概率分布（例如，高斯分布），这可能是由x生成的。在训练期间，我们不断更新权重φ，以
更接近真实的。 -
解码器的目标是逼近真实的概率分布
。换句话说，在给定潜在表示z的情况下，解码器尝试学习数据x的条件概率分布。我们将用 表示解码器对真实概率分布的近似，其中θ是解码器权重。该过程首先从概率分布（例如，高斯）随机（随机）对z进行采样。然后，z通过解码器发送，其输出是x的可能对应值的概率分布 
. 在训练期间，我们不断更新权重θ，以 更接近真实的。
VAE 使用一种特殊类型的损失函数，其中包含两个术语：
第一个是 Kullback-Leibler 散度 (第 1 章，神经网络的基本要素）在概率分布和 预期概率分布之间。在这种情况下，它衡量我们用来表示时丢失了多少信息（换句话说，两个分布有多接近）。它鼓励自动编码器探索不同的重建。第二个是重建损失，它衡量原始输入与其重建之间的差异。它们差异越大，它增加的越多。因此，它鼓励自动编码器以更好的方式重建数据。
为了实现这一点，瓶颈层不会直接输出潜在状态变量。相反，它将输出两个向量，它们描述了每个潜在变量分布的均值和方差：
一旦我们有了均值和方差分布，我们就可以从潜在变量分布中采样一个状态z并将其传递给解码器进行重建。但我们还不能庆祝。这给我们带来了另一个问题：反向传播不适用于我们这里的随机过程。幸运的是，我们可以使用所谓的重新参数化技巧来解决这个问题。首先，我们将从高斯分布（上图中的ε圆）中采样一个与z维度相同的随机向量ε。然后，我们将其移动潜在分布的均值μ， 并通过潜在分布的方差σ 对其进行缩放：
通过这种方式，我们将能够优化均值和方差（红色箭头），并且我们将从后向传递中省略随机生成器。同时，采样数据将具有原始分布的属性。既然我们已经介绍了 VAE，我们将学习如何实现它。
使用 VAE 生成新的 MNIST 数字
在本节中，我们将了解 VAE 如何为MNIST数据集 生成 新数字。我们将使用TF 2.0.0 下的 Keras来执行此操作。我们选择 MNIST 是因为它可以很好地说明 VAE 的生成能力。
让我们逐步完成实现：
1.让我们从进口开始。我们将使用集成在 TF 中的 Keras 模块：
import matplotlib.pyplot as plt
from matplotlib.markers import MarkerStyle
import numpy as np
import tensorflow as tf
from tensorflow.keras import backend as K
from tensorflow.keras.layers import Lambda, Input, Dense
from tensorflow.keras.losses import binary_crossentropy
from tensorflow.keras.models import Model2.现在，我们将实例化 MNIST 数据集。回想一下，在第 2 章，了解卷积网络，我们使用 TF/Keras 实现了一个迁移学习示例，我们使用该tensorflow_datasets模块加载 CIFAR-10 数据集。在这个例子中，我们将使用该keras.datasets模块来加载 MNIST，它也可以工作：
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
image_size = x_train.shape[1] * x_train.shape[1]
x_train = np.reshape(x_train, [-1, image_size])
x_test = np.reshape(x_test, [-1, image_size])
x_train = x_train.astype('float32') / 255
x_test = x_test.astype('float32') / 2553.接下来，我们将实现该函数，该函数将构建 VAE： build_vae
- 我们将分别访问编码器、解码器和整个网络。该函数会将它们作为元组返回。
- 瓶颈层将只有神经元（也就是说，我们只有潜在变量）。通过这种方式，我们将能够将潜在分布显示为 2D 图。 2 2
- 编码器/解码器将包含一个带有神经元的中间（隐藏）全连接层。这不是卷积网络。 512
- 我们将使用交叉熵重建损失和 KL 散度。
下面显示了这是如何在全球范围内实现的：
def build_vae(intermediate_dim=512, latent_dim=2):
# encoder first
inputs = Input(shape=(image_size,), name='encoder_input')
x = Dense(intermediate_dim, activation='relu')(inputs)
# latent mean and variance
z_mean = Dense(latent_dim, name='z_mean')(x)
z_log_var = Dense(latent_dim, name='z_log_var')(x)
# Reparameterization trick for random sampling
# Note the use of the Lambda layer
# At runtime, it will call the sampling function
z = Lambda(sampling, output_shape=(latent_dim,),
name='z')([z_mean, z_log_var])
# full encoder encoder model
encoder = Model(inputs, [z_mean, z_log_var, z], name='encoder')
encoder.summary()
# decoder
latent_inputs = Input(shape=(latent_dim,), name='z_sampling')
x = Dense(intermediate_dim, activation='relu')(latent_inputs)
outputs = Dense(image_size, activation='sigmoid')(x)
# full decoder model
decoder = Model(latent_inputs, outputs, name='decoder')
decoder.summary()
# VAE model
outputs = decoder(encoder(inputs)[2])
vae = Model(inputs, outputs, name='vae')
# Loss function
# we start with the reconstruction loss
reconstruction_loss = binary_crossentropy(inputs, outputs) *
image_size
# next is the KL divergence
kl_loss = 1 + z_log_var - K.square(z_mean) - K.exp(z_log_var)
kl_loss = K.sum(kl_loss, axis=-1)
kl_loss *= -0.5
# we combine them in a total loss
vae_loss = K.mean(reconstruction_loss + kl_loss)
vae.add_loss(vae_loss)
return encoder, decoder, vae4.与网络定义直接相关的是函数，它实现了对来自高斯单元的潜在向量的随机采样（这是我们在VAE 简介部分介绍的重新参数化技巧）： sampling z
def sampling(args: tuple):
"""
:param args: (tensor, tensor) mean and log of variance of
q(z|x)
"""
# unpack the input tuple
z_mean, z_log_var = args
# mini-batch size
mb_size = K.shape(z_mean)[0]
# latent space size
dim = K.int_shape(z_mean)[1]
# random normal vector with mean=0 and std=1.0
epsilon = K.random_normal(shape=(mb_size, dim))
return z_mean + K.exp(0.5 * z_log_var) * epsilon5.现在，我们需要实现该功能。它收集测试集中所有图像的潜在表示，并将它们显示在 2D 图上。我们可以这样做，因为我们的网络只有两个潜在变量（对于图的两个轴）。请注意，要实现这一点，我们只需要： plot_latent_distribution encoder
def plot_latent_distribution(encoder, x_test, y_test, batch_size=128):
z_mean, _, _ = encoder.predict(x_test, batch_size=batch_size)
plt.figure(figsize=(6, 6))
markers = ('o', 'x', '^', '<', '>', '*', 'h', 'H', 'D', 'd',
'P', 'X', '8', 's', 'p')
for i in np.unique(y_test):
plt.scatter(z_mean[y_test == i, 0], z_mean[y_test == i, 1],
marker=MarkerStyle(markers[i],
fillstyle='none'),
edgecolors='black')
plt.xlabel("z[0]")
plt.ylabel("z[1]")
plt.show()6.接下来，我们将实现该功能。它将在两个潜在变量中的每一个的范围内对向量进行采样。接下来，它将根据采样的向量生成图像，并将它们显示在 2D 网格中。请注意，要做到这一点，我们只需要： plot_generated_images n*n z [-4, 4] decoder
def plot_generated_images(decoder):
# display a nxn 2D manifold of digits
n = 15
digit_size = 28
figure = np.zeros((digit_size * n, digit_size * n))
# linearly spaced coordinates corresponding to the 2D plot
# of digit classes in the latent space
grid_x = np.linspace(-4, 4, n)
grid_y = np.linspace(-4, 4, n)[::-1]
# start sampling z1 and z2 in the ranges grid_x and grid_y
for i, yi in enumerate(grid_y):
for j, xi in enumerate(grid_x):
z_sample = np.array([[xi, yi]])
x_decoded = decoder.predict(z_sample)
digit = x_decoded[0].reshape(digit_size, digit_size)
slice_i = slice(i * digit_size, (i + 1) * digit_size)
slice_j = slice(j * digit_size, (j + 1) * digit_size)
figure[slice_i, slice_j] = digit
# plot the results
plt.figure(figsize=(6, 5))
start_range = digit_size // 2
end_range = n * digit_size + start_range + 1
pixel_range = np.arange(start_range, end_range, digit_size)
sample_range_x = np.round(grid_x, 1)
sample_range_y = np.round(grid_y, 1)
plt.xticks(pixel_range, sample_range_x)
plt.yticks(pixel_range, sample_range_y)
plt.xlabel("z[0]")
plt.ylabel("z[1]")
plt.imshow(figure, cmap='Greys_r')
plt.show()7.现在，运行整个代码。我们将使用 Adam 优化器（在第 1 章，神经网络的基本要素中介绍）来训练网络 50 个 epoch：
if __name__ == '__main__':
encoder, decoder, vae = build_vae()
vae.compile(optimizer='adam')
vae.summary()
vae.fit(x_train,
epochs=50,
batch_size=128,
validation_data=(x_test, None))
plot_latent_distribution(encoder, x_test, y_test,
batch_size=128)
plot_generated_images(decoder)8.如果一切按计划进行，一旦训练结束，我们将看到所有测试图像的每个数字类别的潜在分布。左轴和下轴代表潜变量。不同的标记形状代表不同的数字类别： z1 z2
9.接下来，我们将查看由 生成的图像。坐标轴代表用于每个图像的特定潜在分布： plot_generated_images z
我们对 VAE 的描述到此结束。在下一节中，我们将讨论 GAN——可以说是最流行的生成模型家族。
GAN 简介
在本节中，我们将讨论可以说是当今 最 流行的生成模型：GAN 框架。它于 2014 年在具有里程碑意义的论文Generative Adversarial Nets ( http://papers.nips.cc/paper/5423-generation-adversarial-nets.pdf ) 中首次引入。GAN 框架可以处理任何类型的数据，但它目前最流行的应用是生成图像，我们将仅在此上下文中讨论它们。让我们看看它是如何工作的：
GAN 是由两个组件（神经网络）组成的系统：
- 生成器：这是生成模型本身。它以 概率 分布（随机噪声）作为输入，并尝试生成逼真的输出图像。其目的类似于 VAE 的解码器部分。
- 鉴别器：这需要两个 交替 输入：训练数据集的真实图像或从生成器生成的假样本。它试图确定输入图像是来自真实图像还是生成图像。
这两个网络作为一个系统一起训练。一方面，鉴别器试图更好地区分真假图像。另一方面，生成器尝试输出更逼真的图像，以便它可以欺骗鉴别器认为生成的图像是真实的。使用原始论文中的类比，您可以将生成器视为伪造者团队，试图制造假币。反之，鉴别器充当警察，试图抓获假币，两人不断地试图欺骗对方（因此得名对抗性）。该系统的最终目标是让生成器做得很好，以至于判别器无法区分真假图像。即使鉴别器执行分类，GAN 仍然是无监督的，因为我们不需要图像的标签。在下一节中，我们将讨论 GAN 框架背景下的训练过程。
训练 GAN
我们的主要目标是让生成器生成逼真的图像，而 GAN 框架是实现该目标的工具。我们将分别并按顺序（一个接一个）训练生成器和 判别器， 并在两个阶段之间多次交替。
在进入更多细节之前，让我们使用下图来介绍一些符号：
- 我们将用 表示生成器
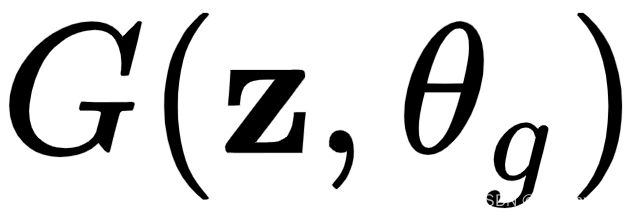，其中
是网络权重，z是潜在向量，用作生成器的输入。将其视为启动图像生成过程的随机种子值。它类似于 VAE 中的潜在向量。z 有一个概率分布 ，
它通常是随机正态或随机均匀的。生成器输出假样本x，其概率分布为 。您可以将其视为根据生成器的真实数据的概率分布。
- 我们将用 表示鉴别器
，其中
是网络权重。它将具有分布的真实数据或生成的样本作为输入。判别器是一个二元分类器，输出输入图像是真实数据（网络输出 1）还是生成数据（网络输出 0）的一部分。
- 在训练期间，我们将分别用 和 表示鉴别器和生成器损失
函数
。
下面是一个更详细的 GAN 框架图：
GAN 训练与训练常规 DNN 不同，因为我们有两个网络。我们可以将其视为两个玩家（生成器和判别器）的顺序极小极大零和游戏：
- Sequential：这意味着玩家一个接一个地 轮流 进行，类似于国际象棋或井字游戏（而不是同时进行）。首先，鉴别器试图最小化，但它只能通过调整权重来做到这一点，。接下来，生成器尝试最小化，但它只能调整权重 ，。我们多次重复这个过程。
- 零和：这意味着一个玩家的收益或 损失 与对方玩家的收益或损失相平衡。即生成器的损失和判别器的损失之和始终为0：
- Minimax：这意味着第一个 玩家 （生成器）的策略是最小化对手（判别器）的最大 分数（因此得名）。当我们在鉴别器中进行训练时，它在区分真假样本方面变得更好（最小化）。接下来，当我们训练生成器时，它会尝试提升到新的和改进的鉴别器的水平（我们最小化，相当于最大化）。这两个网络一直在竞争。我们将用以下公式表示极小极大游戏，其中 是损失函数：
让我们假设，经过一些训练步骤后，两者都 将 处于某个局部最小值。在这里，极小极大博弈的解称为纳什均衡。当其中一个参与者不改变其行为时，无论其他参与者可能做什么，纳什均衡就会发生。当生成器变得非常好以至于鉴别器不再能够区分生成的样本和真实样本时，GAN 框架中的纳什均衡就会发生。也就是说，无论输入如何，鉴别器的输出总是一半。
现在我们已经对 GAN 有了一个概述，让我们讨论如何训练它们。我们将从鉴别器开始，然后我们将继续生成器。
训练判别器
鉴别器是一个分类神经 网络 ，我们可以用通常的方式训练它，即使用梯度下降和反向传播。但是，训练集由真实和生成的样本组成。让我们学习如何将其纳入训练过程：
1.根据输入样本（真实或虚假），我们有两条路径：
- 从真实数据中选择样本
，并用它来生成D(X)。 - 生成假样本，
. 在这里，生成器和鉴别器作为一个单一的网络工作。我们从一个随机向量z开始，我们用它来生成生成的样本
。然后，我们将其用作鉴别器的输入以产生最终输出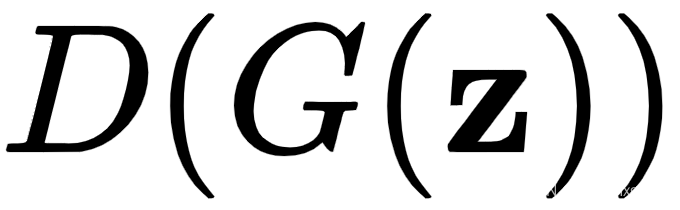
。
2.接下来，我们计算损失函数，它反映了训练数据的对偶性（稍后会详细介绍）。
3.最后，我们反向传播误差梯度并更新权重。尽管这两个网络一起工作，但生成器权重 ,
将被锁定，我们将只更新鉴别器权重 , 
。这确保我们将通过使其更好而不是使生成器变得更糟来提高判别性能。
为了理解判别器损失，让我们回顾一下交叉熵损失的公式：
这里，
是属于第i个类（在n 个总类中）的输出的估计概率，是实际概率。为了简单起见，我们假设我们将公式应用于单个训练样本。在二分类的情况下，这个公式可以简化为：
(one-hot-encoding) 时，损失项之一始终为0。
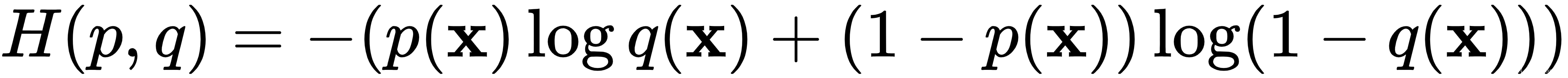
我们可以扩展m个样本的 mini-batch 的公式：
知道了这一切，让我们定义判别器损失：
尽管看起来很复杂，但这只是具有一些 GAN 特定的花里胡哨的二元分类器的交叉熵损失。让我们讨论一下：
- 损失的两个分量反映了两个可能的类别（真实或虚假），它们在训练集中的数量相等。
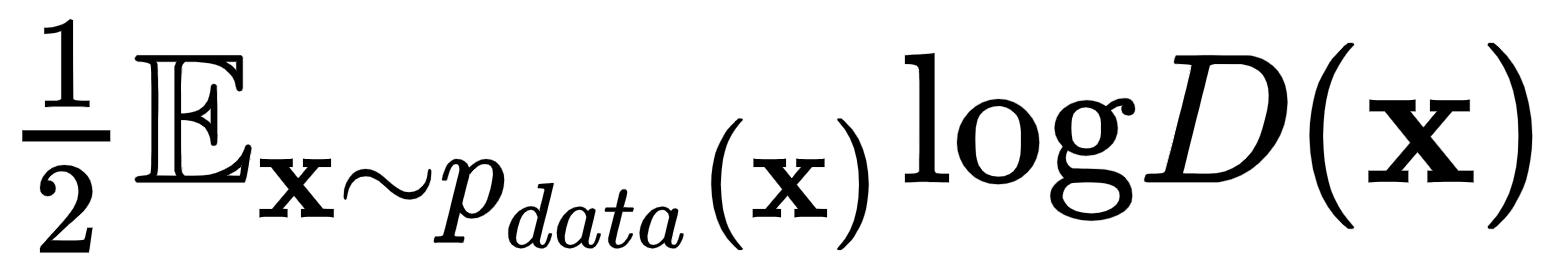是从真实数据中采样输入时的损失。理想情况下，在这种情况下，我们将拥有D(x)=1.- 在这种情况下，期望项
,意味着x是从 
中采样的。本质上，这部分损失意味着，当我们从 中采样x时，我们期望判别器输出。最后，0.5 是真实数据的累积类别概率，因为它正好包含整个集合的一半。 
是从生成的数据中采样输入时的损失。在这里，我们可以进行与真实数据组件相同的观察。但是，当 时，该项最大化
。
总而言之，当
所有
和
所有生成 
（或
）时，鉴别器损失将为零。
训练生成器
我们将通过使其更好地 欺骗 鉴别器来训练生成器。为此，我们需要两个网络，类似于我们用假样本训练鉴别器的方式：
- 我们从一个随机潜在向量z开始，并通过生成器和鉴别器将其输入以产生输出D(G(z))。
- 损失函数与鉴别器损失相同。然而，我们的目标是最大化而不是最小化它，因为我们想要欺骗鉴别器。
- 在后向传递中，鉴别器权重 ,
被锁定，我们只能调整
。这迫使我们通过使生成器更好而不是使鉴别器变得更糟来最大化鉴别器损失。
您可能已经注意到，在这个阶段，我们只使用生成的数据。由于鉴别器的权重是锁定的，我们可以忽略损失函数中处理真实数据的部分。因此，我们可以将其简化为：
这个公式的导数（梯度）是
，在下图中可以看出是一条不间断的线。这对训练施加了限制。早期，当鉴别器可以轻松区分真假样本时（
），梯度将接近于零。这将导致对权重的学习很少，（梯度消失问题的另一种表现形式）：
我们可以通过使用不同的损失函数来解决这个问题：
该函数的导数在上图中用虚线显示。当
并且梯度很大时，这种损失仍然最小化；也就是说，当发电机表现不佳时。有了这个损失，游戏就不再是零和游戏了，但这不会对 GAN 框架产生实际影响。现在，我们拥有了定义 GAN 训练算法所需的所有要素。我们将在下一节中执行此操作。
把它们放在一起
使用我们新发现的知识，我们可以完整地 定义 极小极大目标：
简而言之，生成器试图最小化目标，而鉴别器试图最大化它。请注意，虽然判别器应该最小化其损失，但极小化目标是判别器损失的负数，因此判别器必须使其最大化。
以下逐步训练算法由 GAN 框架的作者介绍。
重复此操作进行多次迭代：
1.重复k步，其中k是一个超参数：
- 从潜在空间中抽取m个随机样本的 mini-batch ，
- 从真实数据中抽取m个样本的 mini-batch ，
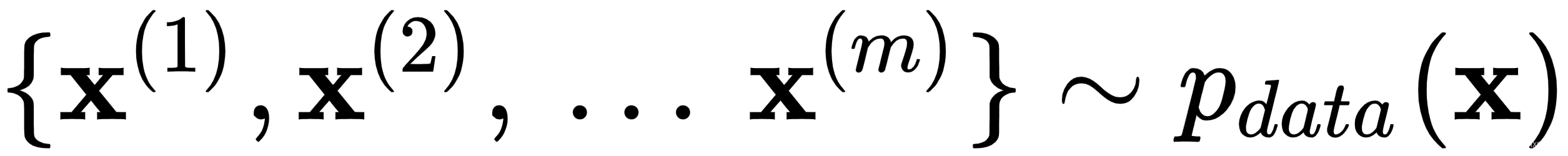
通过提升其成本的随机梯度来更新鉴别器权重：
2.从潜在空间中抽取m个随机样本的 mini-batch ，
。
3.通过降低其成本的随机梯度来更新生成器：
或者，我们可以使用我们在训练生成器部分介绍的更新成本函数：
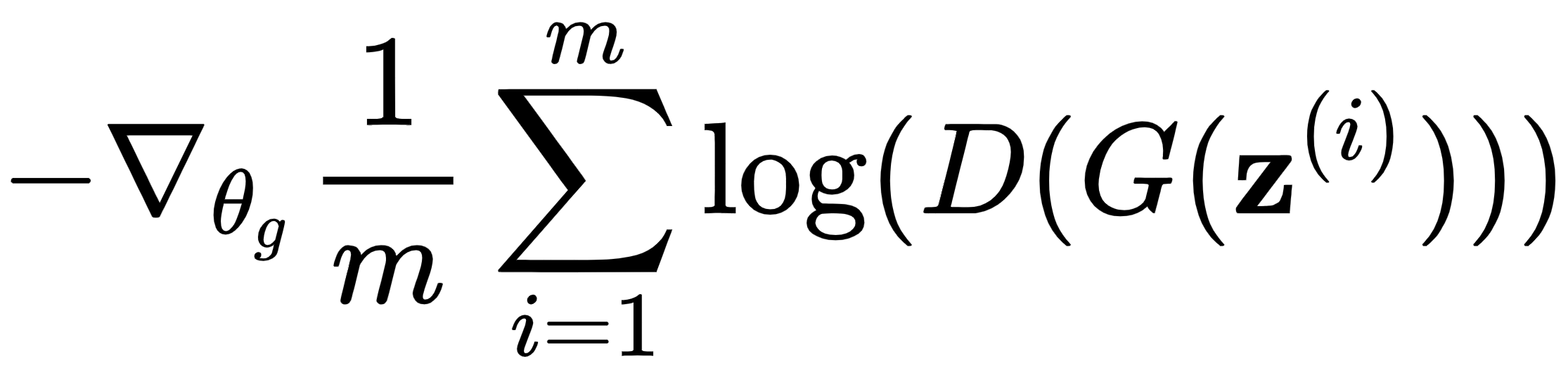
既然我们知道了如何训练 GAN，让我们讨论一下我们在训练它们时可能面临的一些问题。
训练 GAN 的问题
训练 GAN 模型有一些主要的缺陷：
- 梯度下降算法旨在找到损失函数的最小值，而不是纳什均衡，这不是一回事。因此，有时训练可能无法收敛，反而会发生振荡。
- 回想一下，判别器的输出是一个 sigmoid 函数，它表示示例是真还是假的概率。如果判别器在这个任务上做得太好，概率输出将在每个训练样本处收敛到 0 或 1。这意味着误差梯度将始终为 0，这将阻止生成器学习任何东西。另一方面，如果鉴别器在从真实图像中识别假货方面表现不佳，它将向生成器反向传播错误的信息。因此，判别器不应该太好或太差，以至于训练无法成功。在实践中，这意味着我们无法训练它直到收敛。
- 模式崩溃 是一个问题，其中生成器可以生成有限数量的图像（甚至仅一个），而不管潜在输入向量值如何。为了理解为什么会发生这种情况，让我们关注一个单一的生成器训练集，它试图
在鉴别器的权重固定的情况下最小化。换句话说，生成器尝试生成假图像x * ，因此
. 但是，损失函数不会强制生成器为输入潜在向量的不同值创建唯一图像x * 。也就是说，训练可以修改生成器，使其完全解耦生成的图像，x * ，从潜在向量值，同时，仍然最小化损失函数。例如，用于生成新 MNIST 图像的 GAN 只能生成数字 4，而与输入无关。一旦我们更新了鉴别器，之前的值x *可能不再是最优的，这将迫使生成器生成新的和不同的图像。然而，模式崩溃可能会在训练过程的不同阶段再次发生。
现在我们熟悉了 GAN 框架，我们将讨论几种不同类型的 GAN。
GAN 的类型
自从 首次引入 GAN 框架以来，已经出现了许多新的变体。事实上，现在有很多新的 GAN，为了脱颖而出，作者想出了一些富有创意的GAN名称，例如BicycleGAN、DiscoGAN、GANs for LIFE 和 ELEGANT。在接下来的几节中，我们将讨论其中的一些。所有示例均使用 TensorFlow 2.0 和 Keras 实现。
深度卷积GAN
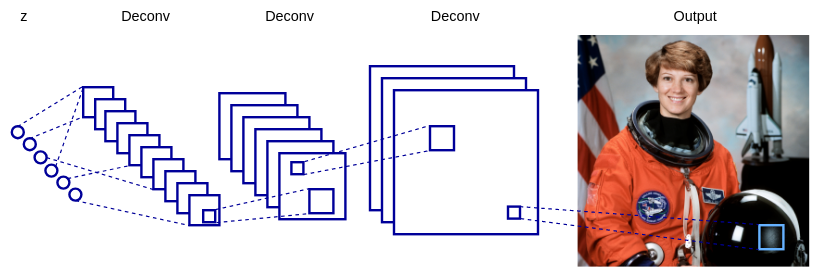
在本节中，我们将实现深度卷积 GAN （DCGAN，具有深度卷积生成对抗网络的无监督表示学习，https://arxiv.rg/abs/1511.06434）。在最初的 GAN框架提案中，作者只使用了全连接网络。相比之下，在 DCGAN 中，生成器和判别器都是 CNN。他们有一些限制，有助于稳定培训过程。您可以将这些视为 GAN 训练的一般指南，而不仅仅是 DCGAN：
- 鉴别器使用跨步卷积而不是池化层。
- 生成器使用转置卷积将潜在向量
上采样到生成图像的大小。 - 两个网络都使用批量标准化。
- 没有全连接层，除了判别器的最后一层。
- 生成器和判别器的所有层的LeakyReLU激活，除了它们的输出。生成器输出层使用 Tanh 激活（范围为 (-1, 1)）来模拟真实世界数据的属性。鉴别器有一个单一的 sigmoid 输出（回想一下，它在 (0, 1) 的范围内），因为它测量了样本是真还是假的概率。
在下图中，我们可以看到DCGAN 框架中的示例 生成器网络：
实施 DCGAN
在本节中，我们将实现 DCGAN，它会生成新的 MNIST 图像。该示例将作为后续部分中所有 GAN 实现的蓝图。让我们开始吧：
1.让我们从导入必要的模块和类开始：
import matplotlib.pyplot as plt
import numpy as np
from tensorflow.keras.datasets import mnist
from tensorflow.keras.layers import \
Conv2D, Conv2DTranspose, BatchNormalization, Dropout, Input,
Dense, Reshape, Flatten
from tensorflow.keras.layers import LeakyReLU
from tensorflow.keras.models import Sequential, Model
from tensorflow.keras.optimizers import Adam2.实现功能。我们将遵循本节开头概述的指南——使用转置卷积、批量归一化和 LeakyReLU 激活进行上采样。该模型从一个全连接层开始，对一维潜在向量进行上采样。然后，使用一系列 对向量进行上采样。final有一个激活，生成的图像只有1个通道： build_generator Conv2DTransposeConv2DTransposetanh
def build_generator(latent_input: Input):
model = Sequential([
Dense(7 * 7 * 256, use_bias=False,
input_shape=latent_input.shape[1:]),
BatchNormalization(), LeakyReLU(),
Reshape((7, 7, 256)),
# expand the input with transposed convolutions
Conv2DTranspose(filters=128, kernel_size=(5, 5),
strides=(1, 1),
padding='same', use_bias=False),
BatchNormalization(), LeakyReLU(),
# gradually reduce the volume depth
Conv2DTranspose(filters=64, kernel_size=(5, 5),
strides=(2, 2),
padding='same', use_bias=False),
BatchNormalization(), LeakyReLU(),
Conv2DTranspose(filters=1, kernel_size=(5, 5),
strides=(2, 2), padding='same',
use_bias=False, activation='tanh'),
])
# this is forward phase
generated = model(latent_input)
return Model(z, generated)3.构建鉴别器。同样，这是一个带有步幅卷积的简单 CNN：
def build_discriminator():
model = Sequential([
Conv2D(filters=64, kernel_size=(5, 5), strides=(2, 2),
padding='same', input_shape=(28, 28, 1)),
LeakyReLU(), Dropout(0.3),
Conv2D(filters=128, kernel_size=(5, 5), strides=(2, 2),
padding='same'),
LeakyReLU(), Dropout(0.3),
Flatten(),
Dense(1, activation='sigmoid'),
])
image = Input(shape=(28, 28, 1))
output = model(image)
return Model(image, output)4.通过实际的 GAN 训练来实现该功能。此函数实现了训练GAN部分的将所有内容放在一起小节中概述的过程。我们将从函数声明和变量的初始化开始： train
def train(generator, discriminator, combined, steps, batch_size):
# Load the dataset
(x_train, _), _ = mnist.load_data()
# Rescale in [-1, 1] interval
x_train = (x_train.astype(np.float32) - 127.5) / 127.5
x_train = np.expand_dims(x_train, axis=-1)
# Discriminator ground truths
real = np.ones((batch_size, 1))
fake = np.zeros((batch_size, 1))
latent_dim = generator.input_shape[1]我们将继续训练循环，我们将一个鉴别器训练集与一个生成器训练集交替进行。首先，我们训练discriminator1 批real_images和 1 批generated_images. 然后，我们discriminator在同一批generated_images. 请注意，我们将这些图像标记为真实图像，因为我们想要最大化discriminator损失。以下是实现（请注意缩进；这仍然是train函数的一部分）：
for step in range(steps):
# Train the discriminator
# Select a random batch of images
real_images = x_train[np.random.randint(0, x_train.shape[0],
batch_size)]
# Random batch of noise
noise = np.random.normal(0, 1, (batch_size, latent_dim))
# Generate a batch of new images
generated_images = generator.predict(noise)
# Train the discriminator
discriminator_real_loss = discriminator.train_on_batch
(real_images, real)
discriminator_fake_loss = discriminator.train_on_batch
(generated_images, fake)
discriminator_loss = 0.5 * np.add(discriminator_real_loss,
discriminator_fake_loss)
# Train the generator
# random latent vector z
noise = np.random.normal(0, 1, (batch_size, latent_dim))
# Train the generator
# Note that we use the "valid" labels for the generated images
# That's because we try to maximize the discriminator loss
generator_loss = combined.train_on_batch(noise, real)
# Display progress
print("%d [Discriminator loss: %.4f%%, acc.: %.2f%%] [Generator
loss: %.4f%%]" % (step, discriminator_loss[0], 100 *
discriminator_loss[1], generator_loss))5.实现一个样板函数 ,plot_generated_images以在训练完成后显示一些生成的图像：
- 创建一个网格（变量）。 nxn figure
- 为每个生成的图像创建随机潜在向量（变量）。 nxn noise
- 生成图像并将它们放置在网格单元中。
- 显示结果。
以下是实现：
def plot_generated_images(generator):
n = 10
digit_size = 28
# big array containing all images
figure = np.zeros((digit_size * n, digit_size * n))
latent_dim = generator.input_shape[1]
# n*n random latent distributions
noise = np.random.normal(0, 1, (n * n, latent_dim))
# generate the images
generated_images = generator.predict(noise)
# fill the big array with images
for i in range(n):
for j in range(n):
slice_i = slice(i * digit_size, (i + 1) * digit_size)
slice_j = slice(j * digit_size, (j + 1) * digit_size)
figure[slice_i, slice_j] = np.reshape
(generated_images[i * n + j], (28, 28))
# plot the results
plt.figure(figsize=(6, 5))
plt.axis('off')
plt.imshow(figure, cmap='Greys_r')
plt.show()6.generator通过包含、discriminator和网络构建完整的 GAN 模型。我们将使用大小为 64 的潜在向量（变量），我们将使用 Adam 优化器运行 50,000 个批次的训练（这可能需要一段时间）。然后，我们将绘制结果： combined latent_dim
latent_dim = 64
# Build the generator
# Generator input z
z = Input(shape=(latent_dim,))
generator = build_generator(z)
generated_image = generator(z)
# we'll use Adam optimizer
optimizer = Adam(0.0002, 0.5)
# Build and compile the discriminator
discriminator = build_discriminator()
discriminator.compile(loss='binary_crossentropy',
optimizer=optimizer,
metrics=['accuracy'])
# Only train the generator for the combined model
discriminator.trainable = False
# The discriminator takes generated image as input and determines validity
real_or_fake = discriminator(generated_image)
# Stack the generator and discriminator in a combined model
# Trains the generator to deceive the discriminator
combined = Model(z, real_or_fake)
combined.compile(loss='binary_crossentropy', optimizer=optimizer)
train(generator, discriminator, combined, steps=50000, batch_size=100)
plot_generated_images(generator)如果一切按计划进行，我们应该会看到 类似 以下内容：
我们对 DCGAN 的讨论到此结束。在下一节中，我们将讨论另一种称为条件 GAN 的 GAN 模型。
Conditional GAN（条件GAN）
条件 GAN（CGAN，Conditional Generative Adversarial Nets，https ://arxiv.org/abs/1411.1784 ）是 GAN 模型的扩展，其中生成器和判别器都接收一些额外的条件输入信息。这可能是当前图像的类或其他一些属性：
例如，如果我们训练一个 GAN 来生成新的 MNIST 图像，我们可以添加一个额外的输入层，其中包含 one-hot 编码图像标签的值。CGAN 的缺点是它们不是严格无监督的，我们需要某种标签才能让它们工作。但是，它们还有其他一些优点：
- 通过使用结构更好的信息进行训练，模型可以学习更好的数据表示并生成更好的样本。
- 在常规 GAN 中，所有图像信息都存储在潜在向量z中。这带来了一个问题：由于可能很复杂，我们对生成图像的属性没有太多控制。例如，假设我们希望我们的 MNIST GAN 生成某个数字；比如说，7。我们将不得不尝试不同的潜在向量，直到我们达到所需的输出。但是使用 CGAN，我们可以简单地将 7 的 one-hot 向量与一些随机z相结合，网络将生成正确的数字。我们仍然可以尝试不同的z值，模型会生成不同版本的数字，即 7。简而言之，CGAN 为我们提供了一种控制（调节）生成器输出的方法。
由于条件输入，我们将修改 minimax 目标以包括条件y，以及：
实施 CGAN
CGAN 实施的蓝图与实施 DCGAN部分中的 DCGAN 示例非常相似。也就是说，我们将实现 CGAN 以生成 MNIST 数据集的新图像。为了简单（和多样性），我们将使用完全连接的生成器和鉴别器。为避免重复，我们将仅展示与 DCGAN 相比修改过的代码部分。您可以在本书的 GitHub 存储库中找到完整的示例。
第一个显着的区别是生成器的定义：
def build_generator(z_input: Input, label_input: Input):
model = Sequential([
Dense(128, input_dim=latent_dim),
LeakyReLU(alpha=0.2), BatchNormalization(momentum=0.8),
Dense(256),
LeakyReLU(alpha=0.2), BatchNormalization(momentum=0.8),
Dense(512),
LeakyReLU(alpha=0.2), BatchNormalization(momentum=0.8),
Dense(np.prod((28, 28, 1)), activation='tanh'),
# reshape to MNIST image size
Reshape((28, 28, 1))
])
model.summary()
# the latent input vector z
label_embedding = Embedding(input_dim=10,
output_dim=latent_dim)(label_input)
flat_embedding = Flatten()(label_embedding)
# combine the noise and label by element-wise multiplication
model_input = multiply([z_input, flat_embedding])
image = model(model_input)
return Model([z_input, label_input], image)尽管它是一个全连接网络，但我们仍然遵循深度卷积 GAN部分中定义的 GAN 网络设计指南。让我们讨论一下我们将潜在向量z_input与条件标签label_input（值从 0 到 9 的整数）结合起来的方式。我们可以看到它label_input是用一个Embedding层转换的。这一层做了两件事：
- 将整数值 ,label_input转换为长度为的 one-hot 表示input_dim
- 使用 one-hot 表示作为全连接层的输入，其大小为output_dim
嵌入层允许我们为每个可能的输入值获得唯一的向量表示。在这种情况下， 的输出label_embedding具有与潜在向量和 的大小相同的维度z_input。在变量中元素乘法的帮助下，label_embedding与潜在向量 相结合，作为网络其余部分的输入。z_inputmodel_input
接下来，我们将关注鉴别器，它也是一个全连接网络，使用与生成器相同的嵌入机制。这一次，嵌入输出大小为np.prod((28, 28, 1))，等于 784（MNIST 图像的大小）：
def build_discriminator():
model = Sequential([
Flatten(input_shape=(28, 28, 1)),
Dense(256),
LeakyReLU(alpha=0.2),
Dense(128),
LeakyReLU(alpha=0.2),
Dense(1, activation='sigmoid'),
], name='discriminator')
model.summary()
image = Input(shape=(28, 28, 1))
flat_img = Flatten()(image)
label_input = Input(shape=(1,), dtype='int32')
label_embedding = Embedding(input_dim=10, output_dim=np.prod(
(28, 28, 1)))(label_input)
flat_embedding = Flatten()(label_embedding)
# combine the noise and label by element-wise multiplication
model_input = multiply([flat_img, flat_embedding])
validity = model(model_input)
return Model([image, label_input], validity)示例代码的其余部分与 DCGAN 示例非常相似。唯一的其他区别是微不足道的——它们说明了网络的多个输入（潜在向量和嵌入）。该plot_generated_images函数有一个附加参数，允许它为随机潜在向量和特定条件标签（在本例中为数字）生成图像。在下面，我们可以看到条件标签 3、8 和 9 的新生成图像：
我们对 CGAN 的讨论到此结束。在下一节中，我们将讨论另一种称为 Wasserstein GAN 的 GAN 模型。
Wasserstein GAN
为了理解 Wasserstein GAN（WGAN，https ://arxiv.org/abs/1701.07875 ），让我们回想一下，在训练 GAN部分，我们用 表示生成器
的概率分布
，用 表示真实数据的概率分布。在训练 GAN 模型的过程中，我们更新了生成器的权重，因此我们 改变了。GAN 框架的目标是收敛到（这也适用于其他类型的生成模型，例如 VAE），即生成的图像的概率分布应该与真实的相同，这将导致逼真的图像。WGAN使用一种新方法来测量两个分布之间的距离，称为 Wasserstein 距离（或地球移动器距离( EMD )）。为了理解它，让我们从下图开始：
方式
为简单起见，我们假设和是离散分布（同样的规则适用于连续分布）。我们可以通过沿x轴向左或向右移动列 (a, b, c, d, e) 来转换成。每次转移 1 个位置的成本为 1。例如，将列a从其初始位置 2 移动到位置 6 的成本为 4。上图的右侧显示了两种执行此操作的方法。在第一种情况下，总成本 = cost(a:2->6) + cost(e:6->3) + cost(b:3->2) = 4 +3 + 1 = 8。在第二种情况下，总成本 = cost(a:2->3) + cost(b:2->1) = 1 + 1 = 2 . EMD 是将一种分布转换为另一种分布所需的最小总成本。因此，在本例中，我们有 EMD = 2。
我们现在对 EMD 是什么有了一个基本的了解，但我们仍然不知道为什么在 GAN 模型中需要使用这个度量。WGAN 论文为这个问题提供了一个详尽但有些复杂的答案。在本节中，我们将尝试解释它。首先，让我们注意生成器从低维潜在向量 开始，然后将其转换为高维生成图像（例如，在 MNIST 的情况下为 784）。图像的输出大小也意味着生成数据的高维分布。然而，它的内在维度（潜在向量，）要低得多。因为这将被排除在高维特征空间的大部分区域之外。另一方面，是真正的高维，因为它不是从潜在向量开始的；相反，它代表了具有丰富性的真实数据。因此，和很有可能不会在特征空间的任何地方相交。
为了理解为什么这很重要，让我们注意我们可以将生成器和鉴别器成本函数（参见训练 GAN部分）转换为 KL 和Jensen-Shannon的函数（JS，https: //en.wikipedia.org/wiki/ Jensen%E2%80%93Shannon_divergence ) 分歧。这些指标的问题在于，当两个分布不相交时，它们提供了零梯度。也就是说，无论两个分布之间的距离是多少（小或大），如果它们不相交，度量将不会提供有关它们之间实际差异的任何信息。但是，正如我们刚刚解释的那样，分布很可能不会相交。与此相反，无论分布是否相交，Wasserstein 距离都有效，这使其成为 GAN 模型的更好候选者。我们可以用下图直观地说明这个问题：
Wasserstein 距离相对于常规 GAN 鉴别器的优势。来源：https://arxiv.org/abs/1701.07875
在这里，我们可以看到两个不相交的高斯分布，和（分别在左侧和右侧）。常规 GAN 鉴别器输出是 sigmoid 函数（范围为 (0, 1)），它告诉我们输入是否为假的概率。在这种情况下，sigmoid 输出在非常窄的范围内（以 0 为中心）有意义，并在所有其他区域收敛到 0 或 1。这是我们在训练 GAN的问题部分中概述的相同问题的体现。它会导致梯度消失，从而防止错误反向传播到生成器。相比之下，WGAN 不会给我们关于图像是真还是假的二元反馈，而是提供两个分布之间的实际距离测量值（也显示在前面的图表中）。这个距离比二元分类更有用，因为它可以更好地指示如何更新生成器。为了反映这一点，该论文的作者将鉴别器重命名为critic 。
以下屏幕截图显示了论文中描述的 WGAN 算法：
这里，f w表示critic，g w是critic 权重更新，g θ是生成器权重更新。尽管 WGAN 背后的理论很复杂，但在实践中，我们可以通过对常规 GAN 模型进行相对较少的更改来实现它：
- 移除鉴别器的输出 sigmoid 激活。
- 用 EMD 派生的损失替换对数生成器/鉴别器损失函数。
- 在每个小批量之后裁剪评论权重，使其绝对值小于常数c 。这个要求对批评者实施了所谓的Lipschitz 约束，这使得使用 Wasserstein 距离成为可能（更多关于这一点的论文本身）。在不深入细节的情况下，我们只会提到重量限制会导致不良行为。这些问题的一个成功解决方案是梯度惩罚（WGAN-GP，Wasserstein GAN 的改进训练，https: //arxiv.org/abs/1704.00028 ），它不会遇到同样的问题。
- 该论文的作者报告说，没有动量的优化方法（SGD，RMSProp）比有动量的优化方法效果更好。
实施 WGAN
现在我们对 Wasserstein GAN 的工作原理有了基本的了解，让我们来实现它。再一次，我们将使用 DCGAN 蓝图并省略重复的代码片段，以便我们可以专注于差异。和函数分别实例化生成器build_generator和build_critic批评者。为简单起见，这两个网络仅包含全连接层。所有隐藏层都有 LeakyReLU 激活。按照论文的指导，生成器有 Tanh 输出激活，而评论家有一个单一的标量输出（虽然没有 sigmoid 激活）。接下来，让我们实现该train方法，因为它包含一些 WGAN 细节。我们将从方法的声明和训练过程的初始化开始：
def train(generator, critic, combined, steps, batch_size, n_critic, clip_value):
# Load the dataset
(x_train, _), _ = mnist.load_data()
# Rescale in [-1, 1] interval
x_train = (x_train.astype(np.float32) - 127.5) / 127.5
# We use FC networks, so we flatten the array
x_train = x_train.reshape(x_train.shape[0], 28 * 28)
# Discriminator ground truths
real = np.ones((batch_size, 1))
fake = -np.ones((batch_size, 1))
latent_dim = generator.input_shape[1]然后，我们将继续训练循环，它遵循我们在本节前面描述的 WGAN 算法的步骤。内部循环critic n_critic为每个训练步骤训练步骤generator。事实上，这是在实施 DCGAN 部分的训练函数中训练和训练的主要区别，其中判别器critic和生成器在每一步交替进行。此外，评论家在每个小批量之后被剪裁。以下是实现（请注意缩进；此代码是函数的一部分）：discriminatorweightstrain
for step in range(steps):
# Train the critic first for n_critic steps
for _ in range(n_critic):
# Select a random batch of images
real_images = x_train[np.random.randint(0, x_train.shape[0],
batch_size)]
# Sample noise as generator input
noise = np.random.normal(0, 1, (batch_size, latent_dim))
# Generate a batch of new images
generated_images = generator.predict(noise)
# Train the critic
critic_real_loss = critic.train_on_batch(real_images, real)
critic_fake_loss = critic.train_on_batch(generated_images,
fake)
critic_loss = 0.5 * np.add(critic_real_loss, critic_fake_loss)
# Clip critic weights
for l in critic.layers:
weights = l.get_weights()
weights = [np.clip(w, -clip_value, clip_value) for w in
weights]
l.set_weights(weights)
# Train the generator
# Note that we use the "valid" labels for the generated images
# That's because we try to maximize the discriminator loss
generator_loss = combined.train_on_batch(noise, real)
# Display progress
print("%d [Critic loss: %.4f%%] [Generator loss: %.4f%%]" %
(step, critic_loss[0], generator_loss))接下来，我们将实现 Wasserstein 损失本身的导数。它是一个 TF 操作，表示网络输出和标签（真或假）的乘积的平均值：
def wasserstein_loss(y_true, y_pred):
"""The Wasserstein loss implementation"""
return tensorflow.keras.backend.mean(y_true * y_pred)现在，我们可以构建完整的 GAN 模型。此步骤类似于其他GAN 模型：
latent_dim = 100
# Build the generator
# Generator input z
z = Input(shape=(latent_dim,))
generator = build_generator(z)
generated_image = generator(z)
# we'll use RMSprop optimizer
optimizer = RMSprop(lr=0.00005)
# Build and compile the discriminator
critic = build_critic()
critic.compile(optimizer, wasserstein_loss,
metrics=['accuracy'])
# The discriminator takes generated image as input and determines validity
real_or_fake = critic(generated_image)
# Only train the generator for the combined model
critic.trainable = False
# Stack the generator and discriminator in a combined model
# Trains the generator to deceive the discriminator
combined = Model(z, real_or_fake)
combined.compile(loss=wasserstein_loss, optimizer=optimizer)最后，让我们开始训练和评估：
# train the GAN system
train(generator, critic, combined,
steps=40000, batch_size=100, n_critic=5, clip_value=0.01)
# display some random generated images
plot_generated_images(generator)运行此示例后，WGAN 将在训练 40,000 个小批量后生成以下图像（这可能需要一段时间）：
我们对 WGAN 的讨论到此结束。在下一节中，我们将讨论如何使用 CycleGAN 实现图像到图像的转换。
使用 CycleGAN 进行图像到图像的转换
在本节中，我们将讨论循环一致对抗网络（CycleGAN，使用循环一致对抗网络的未配对图像到图像转换，https ://arxiv.org/abs/1703.10593 ）及其在图像到图像中的应用图像翻译。引用论文本身，图像到图像的转换是一类视觉和图形问题，其目标是使用一组对齐的图像对来学习输入图像和输出图像之间的映射。例如，如果我们有同一张图像的灰度和 RGB 版本，我们可以训练 ML 算法为灰度图像着色，反之亦然。
另一个例子是图像分割（第 3 章，对象检测和图像分割），其中输入图像被转换为同一图像的分割图。在后一种情况下，我们使用图像/分割图对训练模型（U-Net、Mask R-CNN）。但是，配对训练数据可能不适用于许多任务。CycleGAN 为我们提供了一种在没有配对样本的情况下将图像从源域X转换到目标域Y的方法。下图显示了配对和未配对图像的一些示例：
左：配对的训练样本与对应的源图像和目标图像；右图：未配对的训练样本，其中源图像和目标图像不对应。来源：https://arxiv.org/abs/1703.10593
但是 CycleGAN 是如何做到这一点的呢？首先，该算法假设，虽然两个集合中没有直接对，但两个域之间仍然存在一些关系。例如，这些可能是同一场景但角度不同的照片。CycleGAN 旨在学习这种集合级别的关系，而不是不同对之间的关系。理论上，GAN 模型很适合这项任务。我们可以训练一个生成器
，该生成器生成一个图像
，一个判别器无法与目标图像区分开来
。更具体地说，最优G应该将域 X 转换为与域Y^具有相同分布的域。在实践中，该论文的作者发现这样的转换并不能保证单个输入x和输出y以有意义的方式配对 - 存在无限多个映射G，它们将在 上创建相同的分布Y^。他们还发现，这个 GAN 模型存在熟悉的模式崩溃问题。
CycleGAN 试图用所谓的循环一致性来解决这些问题。为了理解这是什么，假设我们将一个句子从英语翻译成德语。如果我们将句子从德语翻译回英语并到达我们开始的原始句子，则翻译将是循环一致的。在数学环境中，如果我们有一个翻译器和另一个翻译器 ，那么两者应该是
互逆的。
为了解释CycleGAN如何实现循环一致性，我们先从下图说起：
该模型有两个生成器和，以及两个相关的鉴别器，分别是D x和D y（上图中的左侧）。我们先来看看G 。它采用输入图像 ，
并生成
，看起来与域Y中的图像相似。D y旨在区分真实图像和生成的图像
。这部分模型的功能类似于常规 GAN，并使用常规 minimax GAN 对抗性损失：
第一项表示原始图像y，第二项表示由G生成的图像。相同的公式对生成器F有效。正如我们之前提到的，这种损失仅确保与来自Y^的图像具有相同的分布，但不会创建有意义的x和y对. 引用这篇论文：如果容量足够大，网络可以将相同的输入图像集映射到目标域中图像的任何随机排列，其中任何学习的映射都可以产生与目标分布匹配的输出分布。因此，仅对抗性损失不能保证学习函数可以将单个输入x i映射到所需的输出y i。
该论文的作者认为，学习的映射函数应该是循环一致的（上图，中间）。对于每个图像，图像平移周期应该能够将x带回原始图像（这称为前向循环一致性）。G生成一个新图像 ，作为 F 的输入，F又生成一个新图像X^，其中
：
。G和F还应该满足后向循环一致性（上图，右）：
.
这条新路径创建了一个额外的循环一致性损失项：
这测量了原始图像之间的绝对差异，即x和y，以及它们生成的对应物X^和Y^。请注意，这些路径可以被视为联合训练两个自动编码器，
并且
。每个自动编码器都有一个特殊的内部结构：它在中间表示的帮助下将图像映射到自身——将图像转换到另一个域。
完整的 CycleGAN 目标是循环一致性损失和F和G的对抗性损失的组合：
这里，系数 λ 控制两个损失之间的相对重要性。CycleGAN 旨在解决以下极小极大目标：
实施 CycleGAN
此示例包含位于Advanced-Deep-Learning-with-Python/Chapter05/cyclegan at master · PacktPublishing/Advanced-Deep-Learning-with-Python · GitHub的几个源文件。除了TF，代码还依赖tensorflow_addons和imageio包。您可以使用pip软件包安装程序安装它们。我们将为多个训练数据集实现 CycleGAN，所有这些数据集均由论文作者提供。在运行示例之前，您必须借助download_dataset.sh可执行脚本下载相关数据集，该脚本使用数据集名称作为参数。可用数据集的列表包含在文件中。一旦你下载了这个，你可以在类的帮助下访问图像，DataLoader该类位于data_loader.py模块（我们不会在这里包含它的源代码）。可以说，该类可以将标准化图像的小批量和整个数据集加载为数组。我们还将省略通常的导入。 numpy
构建生成器和判别器
首先，我们将实现该build_generator功能。到目前为止，我们看到的 GAN 模型都是从某种潜在向量开始的。但是在这里，生成器的输入是来自其中一个域的图像，输出是来自相反域的图像。按照论文的指导，生成器是一个 U-Net 风格的网络。它有一个下采样编码器、一个上采样解码器以及相应编码器/解码器块之间的快捷连接。我们将从build_generator定义开始：
def build_generator(img: Input) -> Model:U-Net 下采样编码器由许多带有LeakyReLU激活的卷积层组成，然后是InstanceNormalization. 批量和实例规范化之间的区别在于批量规范化在整个小批量中计算其参数，而实例规范化为小批量的每个图像分别计算它们。为清楚起见，我们将实现一个名为 的单独子例程downsampling2d，它定义了一个这样的层。当我们构建网络编码器时，我们将使用这个函数来构建必要的层数（请注意这里的缩进；downsampling2d是定义在 中的子程序build_generator）：
def downsampling2d(layer_input, filters: int):
"""Layers used in the encoder"""
d = Conv2D(filters=filters,
kernel_size=4,
strides=2,
padding='same')(layer_input)
d = LeakyReLU(alpha=0.2)(d)
d = InstanceNormalization()(d)
return d接下来，让我们关注解码器，它不是用转置卷积实现的。相反，输入数据通过该操作进行上采样，该UpSampling2D操作只是将每个输入像素复制为 2 × 2 补丁。接下来是常规卷积以平滑补丁。此平滑输出与skip_input来自相应编码器块的快捷方式（或 ）连接相连接。解码器由许多这样的上采样块组成。为清楚起见，我们将实现一个名为 的单独子例程upsampling2d，它定义了一个这样的块。我们将使用它为网络解码器构建必要数量的块（请注意此处的缩进；upsampling2d是定义在 中的子例程build_generator）：
def upsampling2d(layer_input, skip_input, filters: int):
"""
Layers used in the decoder
:param layer_input: input layer
:param skip_input: another input from the corresponding encoder block
:param filters: number of filters
"""
u = UpSampling2D(size=2)(layer_input)
u = Conv2D(filters=filters,
kernel_size=4,
strides=1,
padding='same',
activation='relu')(u)
u = InstanceNormalization()(u)
u = Concatenate()([u, skip_input])
return u接下来，我们将使用我们刚刚定义的子例程来实现 U-Net 的完整定义（请注意此处的缩进；代码是 的一部分build_generator）：
# Encoder
gf = 32
d1 = downsampling2d(img, gf)
d2 = downsampling2d(d1, gf * 2)
d3 = downsampling2d(d2, gf * 4)
d4 = downsampling2d(d3, gf * 8)
# Decoder
# Note that we concatenate each upsampling2d block with
# its corresponding downsampling2d block, as per U-Net
u1 = upsampling2d(d4, d3, gf * 4)
u2 = upsampling2d(u1, d2, gf * 2)
u3 = upsampling2d(u2, d1, gf)
u4 = UpSampling2D(size=2)(u3)
output_img = Conv2D(3, kernel_size=4, strides=1, padding='same',
activation='tanh')(u4)
model = Model(img, output_img)
model.summary()
return model然后，我们应该实现该build_discriminator功能。我们将在这里省略实现，因为它是一个相当简单的 CNN，类似于前面示例中显示的那些（你可以在本书的 GitHub 存储库中找到它）。唯一的区别是，它不是使用批量规范化，而是使用实例规范化。
把它们放在一起
此时，我们通常会实现该train方法，但由于 CycleGAN 的组件较多，我们将向您展示如何构建整个模型。首先，我们实例化data_loader对象，您可以在其中指定训练集的名称（随意尝试不同的数据集）。所有图像都将调整img_res=(IMG_SIZE, IMG_SIZE)为网络输入的大小，其中IMG_SIZE = 256（您也可以尝试128加快训练过程）：
# Input shape
img_shape = (IMG_SIZE, IMG_SIZE, 3)
# Configure data loader
data_loader = DataLoader(dataset_name='facades',
img_res=(IMG_SIZE, IMG_SIZE))然后，我们将定义优化器和损失权重：
lambda_cycle = 10.0 # Cycle-consistency loss
lambda_id = 0.1 * lambda_cycle # Identity loss
optimizer = Adam(0.0002, 0.5)接下来，我们将创建两个生成器g_XY和g_YX，以及它们对应的鉴别器d_Y和d_X。我们还将创建combined模型来同时训练两个生成器。然后，我们将创建复合损失函数，其中包含一个附加的恒等映射项。您可以在相应的论文中阅读更多相关信息，但简而言之，当将图像从绘画域转换为照片域时，它有助于保持输入和输出之间的颜色组合：
# Build and compile the discriminators
d_X = build_discriminator(Input(shape=img_shape))
d_Y = build_discriminator(Input(shape=img_shape))
d_X.compile(loss='mse', optimizer=optimizer, metrics=['accuracy'])
d_Y.compile(loss='mse', optimizer=optimizer, metrics=['accuracy'])
# Build the generators
img_X = Input(shape=img_shape)
g_XY = build_generator(img_X)
img_Y = Input(shape=img_shape)
g_YX = build_generator(img_Y)
# Translate images to the other domain
fake_Y = g_XY(img_X)
fake_X = g_YX(img_Y)
# Translate images back to original domain
reconstr_X = g_YX(fake_Y)
reconstr_Y = g_XY(fake_X)
# Identity mapping of images
img_X_id = g_YX(img_X)
img_Y_id = g_XY(img_Y)
# For the combined model we will only train the generators
d_X.trainable = False
d_Y.trainable = False
# Discriminators determines validity of translated images
valid_X = d_X(fake_X)
valid_Y = d_Y(fake_Y)
# Combined model trains both generators to fool the two discriminators
combined = Model(inputs=[img_X, img_Y],
outputs=[valid_X, valid_Y,
reconstr_X, reconstr_Y,
img_X_id, img_Y_id])接下来，让我们配置combined模型进行训练：
combined.compile(loss=['mse', 'mse',
'mae', 'mae',
'mae', 'mae'],
loss_weights=[1, 1,
lambda_cycle, lambda_cycle,
lambda_id, lambda_id],
optimizer=optimizer)模型准备好后，我们使用该train函数启动训练过程。根据论文的指南，我们将使用大小为 1 的 mini-batch：
train(epochs=200, batch_size=1, data_loader=data_loader,
g_XY=g_XY,
g_YX=g_YX,
d_X=d_X,
d_Y=d_Y,
combined=combined,
sample_interval=200)最后，我们将实现该train功能。它与之前的 GAN 模型有些相似，但它也考虑了两对生成器和判别器：
def train(epochs: int, data_loader: DataLoader,
g_XY: Model, g_YX: Model, d_X: Model, d_Y: Model,
combined:Model, batch_size=1, sample_interval=50):
start_time = datetime.datetime.now()
# Calculate output shape of D (PatchGAN)
patch = int(IMG_SIZE / 2 ** 4)
disc_patch = (patch, patch, 1)
# GAN loss ground truths
valid = np.ones((batch_size,) + disc_patch)
fake = np.zeros((batch_size,) + disc_patch)
for epoch in range(epochs):
for batch_i, (imgs_X, imgs_Y) in
enumerate(data_loader.load_batch(batch_size)):
# Train the discriminators
# Translate images to opposite domain
fake_Y = g_XY.predict(imgs_X)
fake_X = g_YX.predict(imgs_Y)
# Train the discriminators (original images = real /
translated = Fake)
dX_loss_real = d_X.train_on_batch(imgs_X, valid)
dX_loss_fake = d_X.train_on_batch(fake_X, fake)
dX_loss = 0.5 * np.add(dX_loss_real, dX_loss_fake)
dY_loss_real = d_Y.train_on_batch(imgs_Y, valid)
dY_loss_fake = d_Y.train_on_batch(fake_Y, fake)
dY_loss = 0.5 * np.add(dY_loss_real, dY_loss_fake)
# Total discriminator loss
d_loss = 0.5 * np.add(dX_loss, dY_loss)
# Train the generators
g_loss = combined.train_on_batch([imgs_X, imgs_Y],
[valid, valid,
imgs_X, imgs_Y,
imgs_X, imgs_Y])
elapsed_time = datetime.datetime.now() - start_time
# Plot the progress
print("[Epoch %d/%d] [Batch %d/%d] [D loss: %f, acc: %3d%%]
[G loss: %05f, adv: %05f, recon: %05f, id: %05f] time: %s " \
% (epoch, epochs, batch_i, data_loader.n_batches, d_loss[0],
100 * d_loss[1], g_loss[0], np.mean(g_loss[1:3]),
np.mean(g_loss[3:5]), np.mean(g_loss[5:6]), elapsed_time))
# If at save interval => save generated image samples
if batch_i % sample_interval == 0:
sample_images(epoch, batch_i, g_XY, g_YX, data_loader)训练可能需要一段时间才能完成，但该过程将在sample_interval每批之后生成图像。以下显示了由机器感知中心外观数据库 ( CMP Facade Database ) 生成的一些图像示例。它包含建筑立面，其中每个像素都被标记为多个与立面相关的类别之一，例如窗户、门、阳台等：
我们对 GAN 的讨论到此结束。接下来，我们将关注一种不同类型的生成模型，称为艺术风格迁移。
引入艺术风格转移
在最后一节中，我们将讨论艺术风格的转移。与 CycleGAN 的一种应用类似，它允许我们使用一张图像的风格（或纹理）来再现另一张图像的语义内容。尽管它可以用不同的算法实现，但最流行的方法是在 2015 年的A Neural Algorithm of Artistic Style论文 ( https://arxiv.org/abs/1508.06576 ) 中介绍的。它也被称为神经风格迁移，它使用（你猜对了！）CNN。基本算法在过去几年中得到了改进和调整，但在本节中，我们将探索其原始形式，因为这将为我们理解最新版本提供良好的基础。
该算法将两个图像作为输入：
- 我们要重绘的内容图像( C )
- 我们将使用其样式（纹理）重绘C的样式图像( I )
算法的结果是一个新图像：G = C + S。下面是一个神经风格迁移的例子：
要了解神经风格迁移的工作原理，让我们回顾一下 CNN 学习其特征的分层表示。我们知道初始卷积层学习基本特征，例如边缘和线条。相反，更深的层学习更复杂的特征，例如人脸、汽车和树木。知道了这一点，我们再来看看算法本身：
1.与许多其他任务（例如，第 3 章，对象检测和图像分割）一样，该算法从预训练的 VGG 网络开始。
2.向网络提供内容图像C。提取并存储网络中间的一个或多个隐藏卷积层的输出激活（或特征图或切片）。让我们用Acl表示这些激活，其中l是层的索引。我们对中间层感兴趣，因为其中编码的特征抽象级别最适合这项任务。
3.对样式图像S执行相同操作。这一次，用A s l表示l层的风格激活。我们为内容和样式选择的图层不一定相同。
4.生成单个随机图像（白噪声）G。这个随机图像会逐渐变成算法的最终结果。我们将重复此操作进行多次迭代：
- 通过网络传播G。这是我们将在整个过程中使用的唯一图像。就像我们之前所做的那样，我们将存储所有l层的激活（这里，l是我们用于内容和样式图像的所有层的组合）。让我们用A g l表示这些激活。
- 一方面计算随机噪声激活A g l与另一方面A c l和A s l之间的差异。这些将是我们损失函数 的两个组成部分：
，称为内容损失：这只是所有l层的两次激活之间元素差异的MSE 。
，称为样式损失：这类似于内容损失，但我们将比较它们的gram 矩阵而不是原始激活（我们不会详细讨论）。
- 使用内容损失和风格损失来计算总损失 ，这只是两者的加权和。α 和 β 系数决定了哪些分量将具有更大的权重。
- 将梯度反向传播到网络的起点并更新生成的图像。通过这种方式，我们使G更类似于内容和风格图像，因为损失函数是两者的组合。
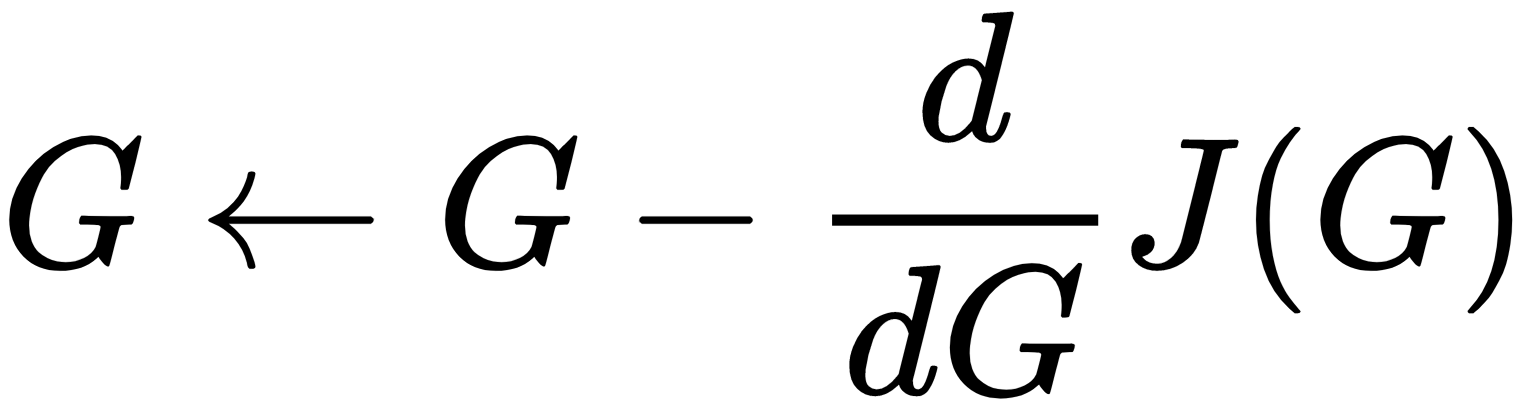
该算法使我们能够利用 CNN 的强大表现力进行艺术风格的迁移。它通过新颖的损失函数和反向传播的智能使用来做到这一点。
如果您对实现神经风格迁移感兴趣，请查看Neural Transfer Using PyTorch — PyTorch Tutorials 1.12.1+cu102 documentation上的官方 PyTorch 教程。或者，转到https://www.tensorflow.org/beta/tutorials/generation/style_transfer了解 TF 2.0 实施。
该算法的一个缺点是它相对较慢。通常，我们必须重复这个伪训练过程几百次迭代才能产生视觉上吸引人的结果。幸运的是，论文Perceptual Losses for Real-Time Style Transfer and Super-Resolution ( https://arxiv.org/abs/1603.08155 ) 建立在原始算法之上，提供了一个解决方案，速度提高了三个数量级。
概括
在本章中，我们讨论了如何使用生成模型创建新图像，这是目前最令人兴奋的深度学习领域之一。我们了解了 VAE 的理论基础，然后我们实现了一个简单的 VAE来生成新的MNIST 数字。然后，我们描述了 GAN 框架，并讨论并实现了多种类型的 GAN，包括 DCGAN、CGAN、WGAN 和 CycleGAN。最后，我们提到了神经风格迁移算法。本章结束了专门介绍计算机视觉的四章系列，我真的希望你喜欢它们。
在接下来的几章中，我们将讨论自然语言处理和循环网络。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
