逻辑回归（Logistic Regression）入门理解与推导

逻辑回归（LR）是一个分类算法，它可以处理二元分类问题和多元分类问题。在介绍LR之前，先回顾一下线性回归（Liner Regression）。

一、线性回归

线性回归是一个回归模型，给定数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } D = \{ ({x_1},{y_1}),({x_2},{y_2}),...,({x_m},{y_m})\} D={(x1​,y1​),(x2​,y2​),...,(xm​,ym​)}，包含 m 个样本，线性回归的假设函数为：

               $h_{\theta }(x)={\theta }_0{x}_0+{\theta }_1{x}_1+...+{\theta }_n{x}_n$

损失函数为：

               $J(\theta )=\frac{1}{2m}\sum _{i=1}^m{[h_{\theta }(x^{(i)})-y^{(i)}]}^2$

带有 L2 正则化的损失函数为：

                J ( θ ) = 1 2 m { ∑ i = 1 m [ h θ ( x ( i ) ) − y ( i ) ] 2 + λ ∑ j = 1 n θ j 2 } J(\theta ) = \frac{1}{{2m}}\{ \sum\limits_{i = 1}^m {{{[{h_\theta }({x^{(i)}}) - {y^{(i)}}]}^2}} + \lambda \sum\limits_{j = 1}^n {{\theta _j}^2} \} J(θ)=2m1​{i=1∑m​[hθ​(x(i))−y(i)]2+λj=1∑n​θj​2}

线性回归的求解可以使用梯度下降法，也可以使用最小二乘法，以下是使用梯度下降法求解的步骤：

（1）初始化参数 $\lambda$，$\epsilon$
（2）确定当前位置损失函数的梯度，对于 ${\theta }_i$，其梯度为：
              $\frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1,...,{\theta }_n)$
（3）用步长 $\lambda$ 乘以梯度，得到下降的距离，即：
              $\lambda \frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1,...,{\theta }_n)$
（4）确定是否对于所有的 ${\theta }_i$，梯度下降的距离都小于 $\epsilon$，如果小于，算法终止；否则执行下一步；
（5）更新所有 ${\theta }_i$：
              ${\theta }_i:={\theta }_i-\lambda \frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1,...,{\theta }_n)$
（6）循环（1）-（5）；

二、逻辑回归推导

由于线性回归模型的输出是连续的实值，而逻辑回归是二分类模型，因此需要把线性回归的实值转换成 0/1 值，在逻辑回归中采用 sigmoid 函数，即：

              $g(z)=\frac{1}{1+e^{-z}}$

这个函数有非常好的特性，即当 z 趋于正无穷时，函数值接近于1；当 z 趋于负无穷时，函数值接近于0，这个特性使它非常适用于 LR 模型，另外它的导数：

              $g^{\prime }(z)=g(z)(1-g(z))$

sigmoid函数的图像如下图：

于是得到 LR 的假设函数：

              $h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$

可以把 $h_{\theta }(x)$ 理解为样本 x 为正样本的概率，那么有：

           $\begin{array}{l}P(y=1|x;\theta )=h_{\theta }(x)\\ P(y=0|x;\theta )=1-h_{\theta }(x)\end{array}$

对于数据集中的 m 个样本来说，有极大似然函数：

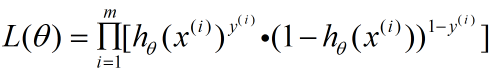
以下是求解极大似然函数的过程，也是导出 LR 模型损失函数的过程：
对上式取负的对数，有：

$J(\theta )=-LnL(\theta )=-\sum _{i=1}^m[(y^{(i)}\log h_{\theta }(x^{(i)})+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)})]$

此式即为LR模型的损失函数，这个函数正好是一个凸函数，可以使用梯度下降法进行求解，参数更新推导如下：

$\frac{\partial }{\partial {\theta }_j}J(\theta )=-(y\frac{1}{h_{\theta }(x)}-(1-y)\frac{1}{1-h_{\theta }(x)})\frac{\partial }{\partial {\theta }_j}{h}_{\theta }(x)$

    $=-\frac{y(1-h_{\theta }(x)-(1-y)h_{\theta }(x))}{h_{\theta }(x)(1-h_{\theta }(x))}\frac{\partial }{\partial {\theta }_j}{h}_{\theta }(x)$

    $=-\frac{y-h_{\theta }(x)}{h_{\theta }(x)(1-h_{\theta }(x))}{h}_{\theta }(x)(1-h_{\theta }(x))\frac{\partial }{\partial {\theta }_j}{h}_{\theta }(x)$

    $=(h_{\theta }(x)-y)x_j$

即更新：

    ${\theta }_j:={\theta }_j-\lambda (h_{\theta }(x^{(i)})-y^{(i)}){x_j}^{(i)}$

根据梯度下降算法的步骤更新即可求解。