作者:JUDGE_MENT
邮箱:gao19920804@126.com
CSDN博客:http://blog.csdn.net/sinat_23137713
最后编辑时间:2016.12.5 V1.1
声明:
1)该资料结合官方文档及网上大牛的博客进行撰写,如有参考会在最后列出引用列表。
2)本文仅供学术交流,非商用。如果不小心侵犯了大家的利益,还望海涵,并联系博主删除。
3)本人才疏学浅,难免出错,还望各位大牛悉心指正。
4)转载请注明出处。
本来是看某博客及论文写的随笔,感觉网上好多的教程写的不清不楚,反正我是有一部分没太看懂,我就只能自己瞎写一下自己的思维过程。如果能帮助到后人一点点也算没有白写。同时毕竟水平有限,其中难免有纰漏。希望有饱含学识之士看到其中的问题之后,可以悉心指出,本人感激不尽。
一、预备知识
1. sigmoid函数 略
2. 贝叶斯定理
P(A)是先验概率,就是在一个事情发生之前我们对他的判断(语音识别:这个字儿是不是'好',根据发音判断这是好的概率就是80%)
P(A|B)是后验概率,就是在事情B发生之后,我们对A发生概率的重新评估(语音识别:假如说识别的之前的字儿是‘你’,在这个前提下再判断这个字儿是'好'的概率)
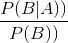
3. MCMC方法:蒙特卡罗马尔科夫
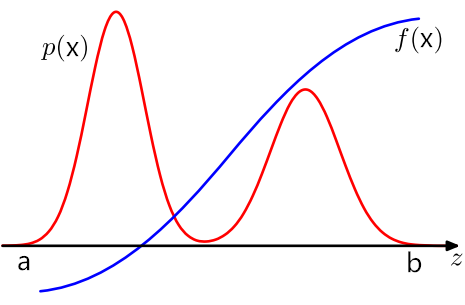
需求:我们要计算某一函数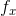
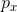
问题:如果我们已经知道变量x的概率分布函数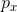
举例:扔骰子。一个不均匀的骰子,你想知道这个骰子的数学期望。问题就是让你估计,所以你根本不知道这个骰子的概率分布是多少,如果你知道具体的期望:投中1的概率20%,投中2概率10%,3概率5%,那你就直接可以计算期望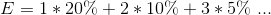
问题:那么,并不知道x具体的概率分布那么怎么办?随机抽取样然后直接求平均就好了。
举例:扔骰子,一直扔,得到一串数字:1,2,4,6,2,3,5,4,2,1.... 那么骰子的数学期望就是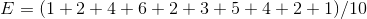
公式化:求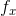
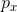
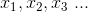
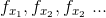
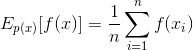
3.1 马尔科夫链
问题:假如说我们已经定义好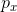
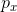
思考:如果是均匀分布/正态分布,有成熟的方式可以采集无偏样本。那么不主流的分布呢?如何采样?
方法:利用马尔科夫链产生指定分布下的样本
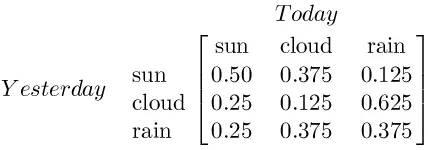
马尔科夫链基础:首先有N个可能的状态:晴天,阴天,雨天;马尔科夫转移矩阵(变量):当前状态转到下一状态的概率;马尔科夫链:预测多个时步下的结果的概率:今天晴,明天阴,后天雨,大后天晴的概率为80%。
马尔科夫链提升:我们知道今天晴天概率为70%,多云概率20%,雨天概率为10%. 则 明天的晴云雨的概率= [70% 20% 10%]*下面的转移矩阵
马尔科夫链最终:如果晴云雨的概率可以一直这么波动且不会转移几次后重复,那么它最终会趋于平稳。我们如果想在某个分布下采样,那么只需以其为平稳分布的马尔科夫过程,经过多次转移之后,我们的样本分布就会充分接近于该平稳分布。
3.2 能量函数的由来-正则分布
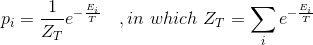
3.3 Metropolis-Hastings采样(用马尔科夫链采样的技术)
当前状态:i --> 根据转移提议分布 --> 计算状态 i --> j 的概率...................................没看明白
3.4 Gibbs采样(用马尔科夫链采样的技术)
Gibbs采样是Metropolis-Hastings的特殊形式,平时用它就足够。
概率抽样:根据概率分布,按比例抽取会发生什么事件。
问题:甲 可以 (吃饭、学习、打球) 在(上午、下午、晚上)天气(晴朗、刮风、下雨),然后我现在要抽取一串样本如“打球+下午+晴朗”..等等..
已知:条件分布已知,好比在(上午+晴天)的条件下,吃饭概率40%学习概率20%打球概率40%。
转移:随便一个初始值,“学习+晚上+刮风” ---->根据条件概率---->三个变量依次修改(可以变成相同的变量)---->“吃饭+上午+刮风".
其他:同样的方法,得到一个序列,每个单元包含三个变量,也就是一个马尔可夫链。然后跳过初始的一定数量的单元(比如100个),然后隔一定的数量取一个单元(比如隔20个取1个)。这样sample到的单元,是逼近联合分布的。
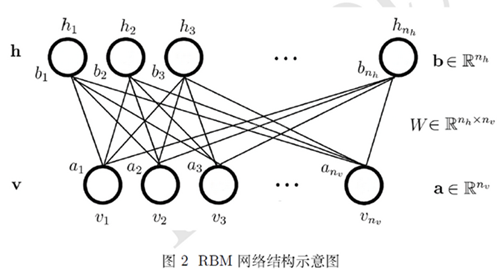
二、网络结构
限制玻尔兹曼机,主要将玻尔兹曼机限制了2点:1.变成二分图 2. 各边内不准连接。
v层:可见层,输入特征。(好比黑白图片,v层就是某处是否为白色)
h层:隐含层
常量: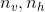
变量: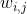
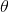
状态:v=(v1,v2,...)T h=(h1,h2,...)T 可见层和隐含层的状态向量
三、能量函数和概率分布
RBM是基于能量的模型。
1. 对于上面网络,给定一组状态( v , h ),自定义一个能量函数:
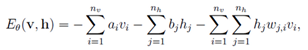
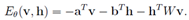
2. 根据正则分布(在上面),用能量函数得到联合概率分布
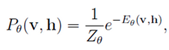
3. 可见层v 的边缘分布与隐含层h的边缘分布(也称似然函数):
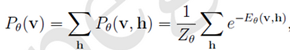
4. 计算某一个神经元为1的条件概率,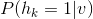 和
和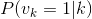 (上面是最主要的部分已经结束,下面的后续用到的推导部分)
(上面是最主要的部分已经结束,下面的后续用到的推导部分)
推倒过程很简单,见 <http://blog.csdn.net/itplus/article/details/19168989>
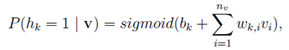
5. 某个可见层得到某个隐含层的概率:为这个隐含层所有神经元为相应的0或1概率的乘积
6. 专家乘积 <a product of experts model>
四、最优化对数似然函数
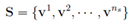 ,每一个
,每一个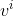 ,都是一个
,都是一个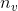 维的向量
维的向量 。
。
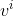 ),这个
),这个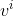 是输入的样本,让这个P(
是输入的样本,让这个P(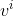 )最大! 所有函数的P都最大,那么就是乘积最大。
)最大! 所有函数的P都最大,那么就是乘积最大。
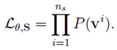
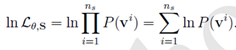
五、梯度计算
问题:计算似然函数时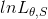
思路:
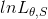
\/
\/
latex码{ lnL_{\theta,S}=\sum_{i=1}^{n_{s}}lnP(v^{i})=\sum_{i=1}^{n_{s}}ln\frac{1}{Z_{\theta }}\sum_{h}e^{-E_{\theta }(v,h))}=\sum_{i=1}^{n_{s}}\{ln\sum_{h}e^{-E({\color{Red} v},h)}-ln\sum_{v,h}e^{-E(v,h)}\} }
解读:分为红色v,是特定的单个训练样本,这是观测到的数据;另一个是黑色的v,其实是归一因子,与具体的观测数据v无关。
\/
\/
要对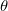
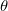
第一个叠加先不看,先对大括号内求导得到:
latex码{ \frac{\partial lnP(v))}{\partial \theta }=-\sum_{h}P(h|v)\frac{\partial E(v,h)}{\partial \theta }+\sum_{v,h}P(v,h)\frac{\partial (v,h)}{\partial \theta } }
\/
\/
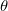
求wij的梯度:
求ai的梯度:
求bi的梯度:
latex代码{ -\sum_{h}P(h|{\color{Red} v})\frac{\partial E({\color{Red} v},h)}{\partial b_{i} }+\sum_{v,h}P(v,h)\frac{\partial (v,h)}{\partial b_{i} }=P(h_{i}=1|{\color{Red} v})-\sum_{v}P(v)P(h_{i}=1|v) }
\/
\/
把原来的叠加大括号再加回去。其实就是有很多的训练数据,然后每个数据计算各梯度,最后全加起来,然后修改相应的w a b。
\/
\/
上面这公式,第一项好求,三.4都把公式写出来了;但是第二项,以w为例,就是函数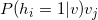
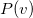
但是难点在于,MCMC采样需要转移次数够多才行。计算复杂度高。
六、对比散度算法
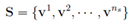 这个v作为出发点(..原来直接是随机的出发点),转移k次就够了,而且之前需要转移1000次之后在
。
这个v作为出发点(..原来直接是随机的出发点),转移k次就够了,而且之前需要转移1000次之后在
。
6.1 过程:
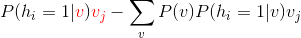 中的第二部分看作求
中的第二部分看作求
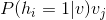 这个函数的
期望(其中v的概率分布为
这个函数的
期望(其中v的概率分布为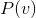 )。既然是求期望就可以用gibbs采样。
)。既然是求期望就可以用gibbs采样。
 作为出发点,以
作为出发点,以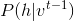 和
和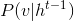 这两个为转移矩阵,计算k步之后的
这两个为转移矩阵,计算k步之后的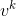 ,然后用这一个代替很多抽取的v。
,然后用这一个代替很多抽取的v。
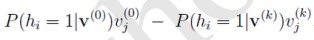
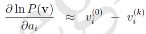 和
和 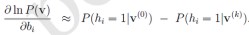
6.2 流程:
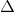 W,
W, 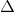 a,
a, 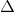 b)
b)
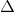 W=0,
W=0, 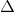 a=0,
a=0, 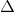 b=0
b=0
 S DO
S DO


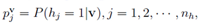

七、RBM训练算法

7.1 将S分成包含几十或几百个样本的小批量数据

7.2 权重和偏置的初始值
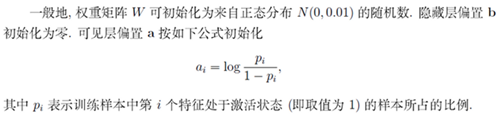
7.3 学习率和动量学习率

7.4 CD-k算法中的参数k
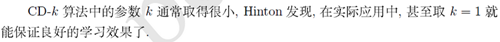
7.5 可见层和隐含层的单元数目nv,nh
八、RBM的评估
8.1 近似方法:重构误差:以训练样本作为初始状态,经过RBM的分布进行一次Gibbs转移后与原数据的差异量。

范数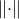
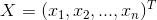
重构误差能够在一定程度上反映RBM对训练样本的似然度,不过并不完全可靠。但总的来说,计算相当简单,因此在实践中非常有用。
另外还有一种叫做退火式重要性抽样(Annealed Importance Sampling, AIS),它通过引入一个更简单的辅助分布,近似计算出归一化因子,从而直接算出RBM对训练数据的似然度,具体参考 <基于马尔科夫链蒙特卡罗方法的RBM学习算法改进,胡洋,2012>
参考:
<1> http://blog.csdn.net/itplus/article/details/19408773
<2> http://www.cnblogs.com/daniel-D/p/3388724.html








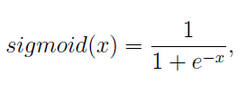
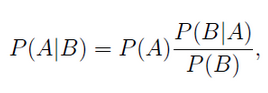
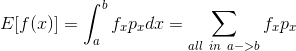
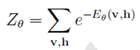
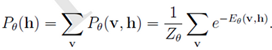

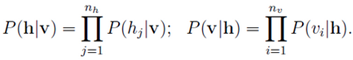
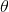
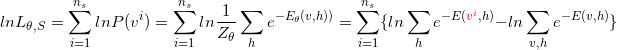

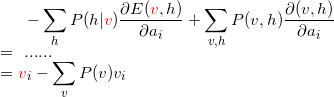
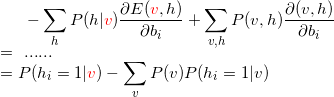
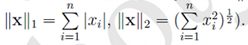














 926
926

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








