KMP字符串匹配算法

最近看了《算法（第4版）》（谢路云 译）上关于Knuth-Morris-Pratt（以下简称KMP）子字符串查找算法的介绍，看完之后不能清晰地理解算法的意思，特别是生成DFA二维数组那段代码，尽管只有短短数行，但却不明其义。几经思考，略有所解，现将一些想法记录下来。文中将待匹配的两字符串分别称为模式（pattern）和文本(text)，在文本中查找模式是否存在。

1. KMP算法相较于暴力匹配法的优势在于文本指针不用回退。以模式为ABACAC为例。

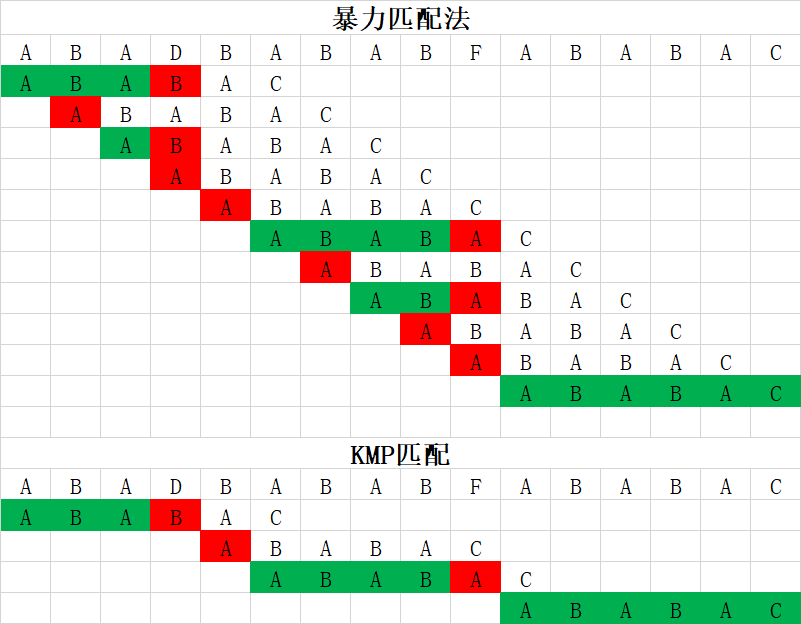
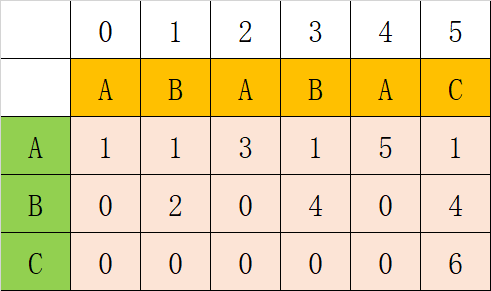
暴力匹配法，每当遇到匹配失败（红色）时，文本指针回退到开始匹配位置右边一位，在这个例子中，文本长度为16，一共比较了26次（绿色和红色，未着色部分未参与比较）。而在KMP算法里，匹配次数仅为文本长度N。KMP匹配时文本指针之所以不回退，是因为提前建立了一个状态表dfa[][]，对于模式ABABAC来讲，DFA二维数组的内容如下

这个表怎么使用呢？第一列的A、B、C以及其他没列出来的字符都是指文本中的字符，第一行自然指模式中的字符，当文本中的字符X与模式中的第i个字符pat[i]比较时，则文本中的下一个字符与第dfa[X][i]比较。如文本中字符为A，与第0个比较，则下一个文本与dfa[A][0]=1比较；如果文本中字符为F，与第3个比较，因为dfa[F][0]=0，故下一个文本又与第0个比较。当dfa[][]的值为模式的长度时，匹配成功。由于文本的指针不会回退，故大大减少了匹配次数。

2. 理解KMP算法的一个典型示例。

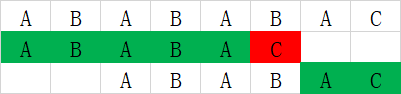
如上图所示，在ABABABAC中查找ABABAC，当第一次匹配失败时，根据状态表dfa[B][5]=4，所以下一个文本字符A直接与pat[4]比较即可。这个表是怎么生成的呢？这里要引入一个“公共前后缀”的概念。在上图中，当匹配失败时，我们已经检查了ABABAB这一串字符，这一串字符的后缀与模式的前缀最大重合部分是ABAB，由于这一截与模式的前一截是一样的，就相当于模式的前面4个字符已经匹配到了，下一个文本字符与pat[4]比较即可。

3. 如何生成DFA状态表？

还是以模式ABABAC为例，可以肯定的是dfa[pat[j]][j] = j + 1. 即第j个匹配成功了，文本下一个字符匹配pat[j+1]。关键是匹配失败了，如何处理。当前缀AB到B匹配失败，说明文本为AX（X为代指，X不为B），当X不是A时，那么这段文本与模式的前缀无重合部分，故下一个文本字符与pat[0]比较；当X为A时，前后缀重合部分为1，下一个与pat[1]比较，即与dfa[][0]一致。

再如，当ABA匹配失败，说明文本为ABX（X不等于A），由于最长公共前后缀为0，故匹配失败的状态仍与dfa[][0]一致。

又如，当ABAB匹配失败，说明文本为ABAX（X不等于B），可以看到ABA的公共前后缀长度为1，说明在比较X与B时，上一个A已经与pat[0]匹配上了，所以在pat[3]处匹配失败的做法与在pat[1]处匹配失败的做法一致，即dfa[][3]=dfa[][1]。

由此可以推知dfa[][n]=dfa[][m]，m为前n个字符的公共前后缀长度，而公共前后缀长度是在可以前面已有的dfa表里获得的，如ABA的公共前后缀长度1 = dfa[A][0]，ABAB的公共前后缀长度为2 = dfa[B][1]，ABABA的公共前后缀长度为3 = dfa[A][2]。由此可知，匹配失败时的状态可以递归地从前面的状态获得。

4. 代码实现。

KMP算法的Java实现在书上是现成的，我写了一份C++实现代码，在leetcode上提交成功了，代码如下

class Solution {
public:
    int strStr(string txt, string pat) {
        int Tlen = txt.length(), Plen = pat.length();
        if(txt == pat || Plen == 0) return 0;
        if (Tlen <= Plen || Tlen == 0) return -1;
       
        vector<vector<int>> dfa(Plen, vector<int>(256, 0));
	    dfa[0][(int)pat[0]] = 1;
	    for (int i = 1, X = 0; i < Plen; i++) {
		    dfa[i] = dfa[X];            
		    dfa[i][(int)pat[i]] = i + 1;
		    X = dfa[X][(int)pat[i]];
	    }
	    int i, j;
	    for (i = 0, j = 0; i < Tlen && j < Plen; i++) {
		    j = dfa[j][(int)txt[i]];
	    }
	    if (j == Plen) return i - Plen;
	    else return -1;
    }
};