《Python数据分析与挖掘实战》这本书其实已经在暑假结束的时候就已经基本上过了一遍,但是却一直没有坚持着记录。最近几天想着将之前的学习内容整理一遍,因此,再做记录。
全文分为以下三个部分:
- Apriori算法
- Apriori的python实现
- 总结
Apriori算法
首先先对Apriori算法的理论知识进行梳理。由于《Python数据分析与挖掘实战》主要针对实战,因此,对理论部分阐述并不多,本文理论知识主要来自于《数据挖掘概念与技术》。
频繁模式、项集和关联规则
频繁模式是频繁地出现在数据集中的模式(如项集、子序列或子结构)。例如,频繁地同时出现在交易数据集中的商品(如牛奶和面包)便是一个频繁项集,而频繁地出现在购物数据库中的序列数据(比如先买PC,再买数码相机,再买内存卡)则是频繁子序列。
项集是项的集合,包含k个项的项集称为k项集,如I={
i1,i2,……,im
}就是一个m项集。
关联规则指的是,项集中每个元素频繁关联或同时出现的模式。具体的,设I={
i1,i2,……,im
}是项的集合,则关联规则是形如A=>B的蕴涵式,其中A和B都是I的子集,且A、B都不为空,A、B的交集为空。
比如,下例表示的就是购买计算机之后又同时购买财务管理软件的关联规则。
支持度、置信度、频繁项集和强关联规则
支持度和置信度是规则兴趣度的两种度量,分别反映所发现规则的有用性和确定性。比如针对上面的举例规则,假设其支持度为2%,置信度为60%,则前者表示分析的所有事务的2%同时购买计算机和财务管理软件(每一个事务是一个非空项集,是上述提到I的子集,所有事务的集合是事务集,构成关联规则发现的事务数据库。),后者表示购买计算机的顾客60%也购买了财务管理软件。
具体用公式表示如下:
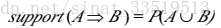
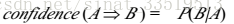
如果项集I的相对支持度(上述公式有时称为相对支持度,而项集的出现频度称为绝对支持度)满足预定义的最小支持阈值(即I的绝对支持度满足对应的最小支持度计数阈值),则I是频繁项集。
满足最小支持度和最小置信度的关联规则,是强关联规则。
Apriori算法-频繁项集挖掘
Apriori算法是一种发现频繁项集的基本算法。其使用一种称为逐层搜索的迭代方法,其中k项集用于探索(k+1)项集。首先,通过扫描数据库,累计每个项的计数,并收集满足最小支持度的项,找出频繁1项集的集合。该集合记为L1。然后。使用L1找出频繁2项集的集合L2,使用L2找出L3,如此下去,直到不能再找到频繁k项集。
为了压缩搜索空间,提出先验性质:频繁项集的所有非空子集也一定是频繁的。(如果一个集合不能通过测试,则他的所有超集也都不能通过相同的测试)
如何使用 Lk−1 找出 Lk (k≥2)
分为两步——连接步和剪枝步。
- 连接步:为找出 Lk ,通过将 Lk−1 与自身连接产生候选k项集的集合。Apriori算法假定项集中的项按照字典序排序。设 l1 和 l2 是 Lk−1 中的项集,如果 l1 和 l2 的前(k-2)个项是相同的,则称 l1 和 l2 是可连接的。所以 l1 与 l2 连接产生的结果项集是{ l1[1] , l1[2] , …, l1[k−1] , l2[k−1] }。
- 剪枝步:由于存在先验性质:任何非频繁的(k-1)项集都不是频繁k项集的子集。因此,如果一个候选k项集 Ck 的(k-1)项子集不在 Lk−1 中,则该候选也不可能是频繁的,从而可以从 Ck 中删除,获得压缩后的 Ck 。
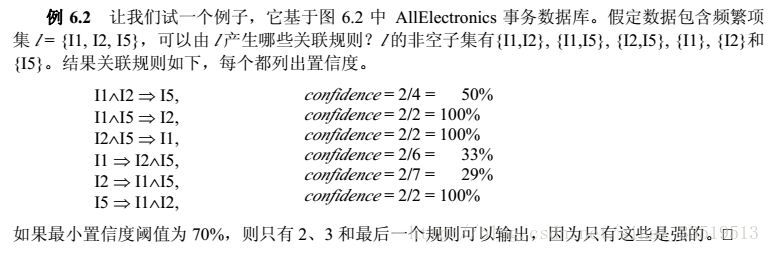
将《数据挖掘概念与技术》中的Apriori例子摘录如下:
该例基于图6.2的数据库,该数据库一共有9个事务。
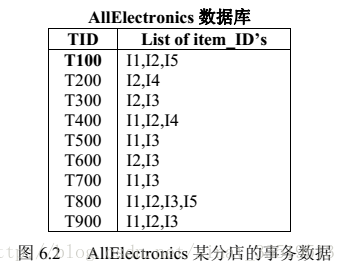



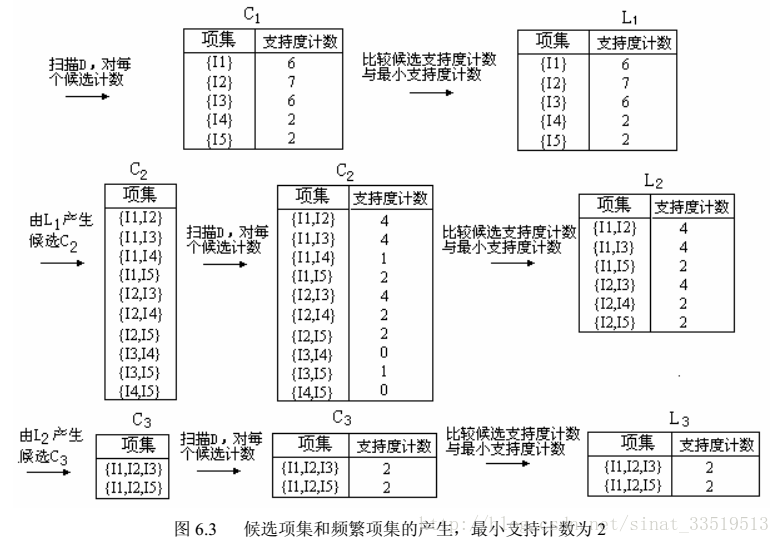

由频繁项集产生关联规则
可直接由频繁项集产生强关联规则:
- 对于每个频繁项集l,产生l的所有非空子集。
- 对于l的每个非空子集s,如果 support_count(t)support_count(s) ≥min_conf(最小置信度),则输出规则”s=>(l-s)”。min_conf为最小置信度阈值。
其中置信度公式完整如下:
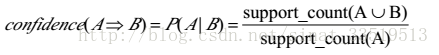
继续上一个例子,摘录如下:
Apriori的python实现
《Python数据分析与挖掘实战》中给出了Apriori的实现代码。
具体代码如下:
import pandas as pd
#自定义连接函数,用于实现L_{k-1}到C_k的连接
def connect_string(x, ms):
x = list(map(lambda i:sorted(i.split(ms)), x))
l = len(x[0])
r = []
for i in range(len(x)):
for j in range(i,len(x)):
if x[i][:l-1] == x[j][:l-1] and x[i][l-1] != x[j][l-1]:
r.append(x[i][:l-1]+sorted([x[j][l-1],x[i][l-1]]))
return r
#寻找关联规则的函数
def find_rule(d, support, confidence, ms = u'--'):
result = pd.DataFrame(index=['support', 'confidence']) #定义输出结果
support_series = 1.0*d.sum()/len(d) #支持度序列
column = list(support_series[support_series > support].index) #初步根据支持度筛选
k = 0
while len(column) > 1:
k = k+1
print(u'\n正在进行第%s次搜索...' %k)
column = connect_string(column, ms)
print(u'数目:%s...' %len(column))
sf = lambda i: d[i].prod(axis=1, numeric_only = True) #新一批支持度的计算函数
#创建连接数据,这一步耗时、耗内存最严重。当数据集较大时,可以考虑并行运算优化。
d_2 = pd.DataFrame(list(map(sf,column)), index = [ms.join(i) for i in column]).T
support_series_2 = 1.0*d_2[[ms.join(i) for i in column]].sum()/len(d) #计算连接后的支持度
column = list(support_series_2[support_series_2 > support].index) #新一轮支持度筛选
support_series = support_series.append(support_series_2)
column2 = []
#遍历可能的推理,如{A,B,C}究竟是A+B-->C还是B+C-->A还是C+A-->B?
for i in column:
i = i.split(ms)
for j in range(len(i)):
column2.append(i[:j]+i[j+1:]+i[j:j+1])
cofidence_series = pd.Series(index=[ms.join(i) for i in column2]) #定义置信度序列
for i in column2: #计算置信度序列
cofidence_series[ms.join(i)] = support_series[ms.join(sorted(i))]/support_series[ms.join(i[:len(i)-1])]
for i in cofidence_series[cofidence_series > confidence].index: #置信度筛选
result[i] = 0.0
result[i]['confidence'] = cofidence_series[i]
result[i]['support'] = support_series[ms.join(sorted(i.split(ms)))]
result = result.T.sort_values(['confidence','support'], ascending = False) #结果整理,输出
print(u'\n结果为:')
print(result)
return result通过分析上述代码,可以发现,上述代码并没有利用先验性质进行剪枝步。
利用上述函数,对数据进行处理。
代码如下:
inputfile = 'D:/ProgramData/PythonDataAnalysiscode/chapter8/demo/data/apriori.txt' #输入事务集文件
data = pd.read_csv(inputfile, header=None, dtype = object)
start = time.clock() #计时开始
print(u'\n转换原始数据至0-1矩阵...')
ct = lambda x : pd.Series(1, index = x[pd.notnull(x)]) #转换0-1矩阵的过渡函数
b = list(map(ct, data.as_matrix())) #用map方式执行
data = pd.DataFrame(b).fillna(0) #实现矩阵转换,空值用0填充
end = time.clock() #计时结束
print(u'\n转换完毕,用时:%0.2f秒' %(end-start))
del b #删除中间变量b,节省内存
support = 0.06 #最小支持度
confidence = 0.75 #最小置信度
ms = '---' #连接符,默认'--',用来区分不同元素,如A--B。需要保证原始表格中不含有该字符
start = time.clock() #计时开始
print(u'\n开始搜索关联规则...')
find_rule(data, support, confidence, ms)
end = time.clock() #计时结束
print(u'\n搜索完成,用时:%0.2f秒' %(end-start))输出结果如下:

由结果也可以看出,本书中对于Apriori算法的实现尚有不足,不仅没有利用到剪枝步,最后的结果中也没有明确究竟是怎样的规则。
最后博主查找其他资料,参考了Apriori(Python实现)这篇文章中的Python代码。
输出结果(部分)如下:
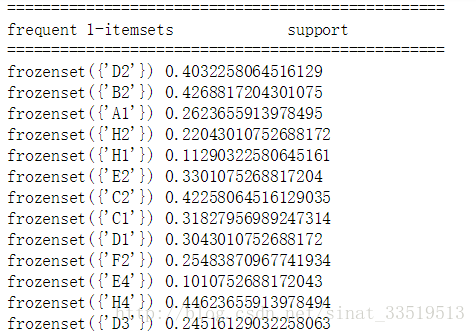

利用这位作者的代码对书中的数据集进行实战,结果跟书中最后实现是一样的,但是过程更加清晰,且最后的规则展现也更加明确。
总结
本文主要结合了《数据挖掘概念与技术》的理论内容和《Python数据分析与挖掘实战》的实战内容,最后又参考了其他人的python实现代码。
对关联规则理论部分有了较好的理解,但是对代码实现部分,还需要再反复揣摩理解一下。
至此,对第八章关联规则部分整理完毕。








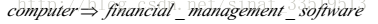















 944
944











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








